
- •Алгебра та початки аналізу Частина іі
- •Харків 2011 Передмова
- •Розділ 1 Тригонометричні функції числового аргументу
- •§1 Радіанна міра вимірювання кутів
- •§2 Тригонометричні функції числового аргументу
- •§3 Властивості тригонометричних функцій
- •§4 Основні тригонометричні тотожності
- •§5 Формули зведення
- •§6 Основні формули тригонометрії
- •§7 Властивості та графіки тригонометричних функцій Властивості і графік функції
- •Властивості і графік функції
- •Властивості і графік функції
- •Властивості та графік функції
- •§8 Обернені тригонометричні функції
- •§9 Розв’язання найпростіших тригонометричних рівнянь
- •§ 10 Розв’язання тригонометричних рівнянь
- •§ 11 Розв’язання тригонометричних нерівностей
- •Розділ 2 Похідна функції та її застосування
- •§ 12 Приріст функції в точці. Похідна функції та її механічний зміст
- •§ 13 Похідна степеневої функції
- •§14 Похідна суми, різниці, добутку та частки двох функцій Правила диференціювання
- •§15 Похідна складеної функції
- •§ 16 Похідні тригонометричних функцій
- •§ 17 Похідна показникової функції
- •§ 18 Похідна логарифмічної функції
- •§ 19 Геометричний зміст похідної
- •§ 20 Похідні вищих порядків
- •§ 21 Диференціал функції і його застосування до наближених обчислень
- •§ 22 Ознака сталості, зростання та спадання функції.
- •§ 23 Екстремум функції
- •§ 24 Побудова графіків функцій Загальна схема для побудови графіків функцій
- •§ 25 Найменше та найбільше значення функції
- •Розділ 3 Інтеграл та його застосування
- •§ 26 Первісна функції. Невизначений інтеграл та його властивості
- •Основні властивості невизначених інтегралів
- •Основні формули інтегрування
- •§ 27 Визначений інтеграл та його властивості
- •Основні властивості визначеного інтегралу:
- •§ 28 Площа криволінійної трапеції
- •§ 29 Застосування визначеного інтеграла при розв’язанні фізичних задач
- •Розділ 4 Елементи теорії ймовірностей і математичної статистики
- •§ 30 Елементи комбінаторики
§2 Тригонометричні функції числового аргументу
Тригонометричним
колом
називається коло центр якого знаходиться
у початку координат, а радіус дорівнює
одиниці. Осі абсцис (Ох) і ординат (Оу)
ділять одиничне коло на чотири чверті(І
– IV),
або чотири квадранта. Відзначимо на осі
Ох справа від початку координат точку
![]() ,
яка лежить на тригонометричному колі:
,
яка лежить на тригонометричному колі:
![]() .
Радіус
.
Радіус
![]() називається початковим радіусом. При
повороті початкового радіуса
називається початковим радіусом. При
повороті початкового радіуса
![]() біля центра О на кут
біля центра О на кут
![]() точка
точка
![]() переходить в деяку точку
переходить в деяку точку
![]() .
.
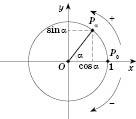 рис.1
рис.1
Синусом
кута
![]() називається відношення ординати точки
називається відношення ординати точки
![]() до радіусу, а косинусом
кута
до радіусу, а косинусом
кута
![]() називається відношення абсциси точки
називається відношення абсциси точки
![]() до радіусу. Оскільки
до радіусу. Оскільки
![]() ,
то
,
то
![]() ,
а
,
а![]() .
.
Оскільки координати
будь-якої точки
![]() одиничного
кола задовольняють рівнянню кола,
одиничного
кола задовольняють рівнянню кола,
![]() .
Співвідношення
.
Співвідношення
![]() називається
основною
тригонометричною тотожністю.
називається
основною
тригонометричною тотожністю.
Тангенсом
кута
![]() називається відношення ординати точки
називається відношення ординати точки
![]() до її абсциси:
до її абсциси:
![]() .
.
Котангенсом
кута
![]() називається відношення абсциси точки
називається відношення абсциси точки
![]() до її ординати:
до її ординати:
![]() .
.
Секансом кута
![]() називається величина, обернена
називається величина, обернена
![]() ,
тобто
,
тобто
![]() .
.
Косекансом
кута
![]() називається величина, обернена
називається величина, обернена
![]() ,
тобто
,
тобто
![]() .
.
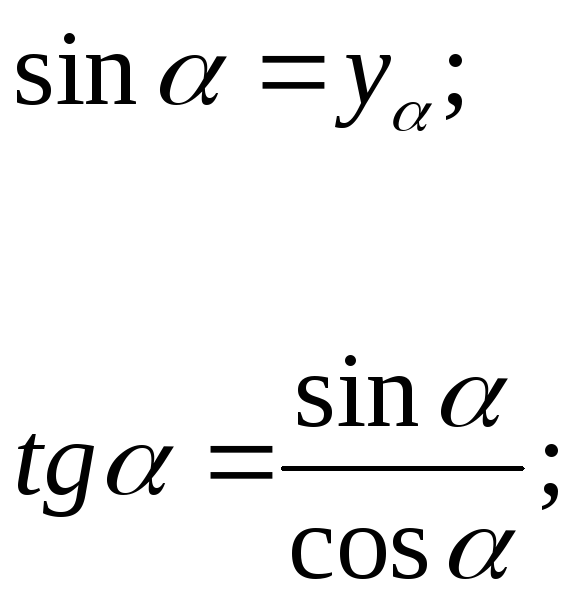

![]()
![]()
Знаки
тригонометричних функцій
![]() ,
,
![]() ,
,
![]() ,
,
![]() у різних чвертях подано у табл. 1
у різних чвертях подано у табл. 1
Таблиця 1
|
|
І |
ІІ |
ІІІ |
ІV |
|
|
+ |
+ |
- |
- |
|
|
+ |
- |
- |
+ |
|
|
+ |
- |
+ |
- |
|
|
+ |
- |
+ |
- |
Зобразимо таблицю значень тригонометричних функцій деяких кутів, які найбільш часто використовуються на практиці (табл. 2).
Таблиця 2
|
|
0 |
|
|
|
|
|
|
|
|
0 |
30 |
45 |
60 |
90 |
180 |
270 |
360 |
|
|
|
0 |
|
|
|
1 |
0 |
-1 |
0 |
|
|
1 |
|
|
|
0 |
-1 |
0 |
1 |
|
|
0 |
|
1 |
|
|
0 |
|
0 |
|
|
|
|
1 |
|
0 |
|
0 |
|
9. На
тригонометричному колі побудувати кут
повороту, що дорівнює:
![]() .
.
10.
Визначити, кутом якої чверті є кут
![]() ,
якщо кут
,
якщо кут
![]() дорівнює:
дорівнює:
![]() .
.
11.
Серед кутів повороту
![]() знайти такі, при яких початковий
радіус-вектор займе таке саме положення,
як і при повороті на кут:
знайти такі, при яких початковий
радіус-вектор займе таке саме положення,
як і при повороті на кут:
1)
![]()
2)
![]() .
.
12. Позначити на одиничному колі точки, які відповідають числам:
1)
![]() ,
де
,
де
![]() ;
;
2)
![]() ,
де
,
де
![]() .
.
13. Одиничний
радіус-вектор
![]() при поверненні на кут
при поверненні на кут
![]() має координати
має координати
![]() .
Знайти
.
Знайти
![]() .
.
14.
Одиничний радіус-вектор
![]() при поверненні на кут
при поверненні на кут
![]() має координати
має координати
![]() .
Знайти
.
Знайти
![]() .
.
15. Обчислити:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)
![]() ;
;
11)
![]() ;
12)
;
12)
![]() .
.
16. Знайти значення виразу:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)
![]() ;
;
11)
 ;
12)
;
12)
![]() .
.
17. Знайти найбільше та найменше значення виразу:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() .
.
18. Визначити знак виразу:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)
![]() ;
;
11)
![]() ;
12)
;
12)
![]() ;
;
13)
![]() ;
14)
;
14)
![]() .
.
