
- •Алгебра та початки аналізу Частина іі
- •Харків 2011 Передмова
- •Розділ 1 Тригонометричні функції числового аргументу
- •§1 Радіанна міра вимірювання кутів
- •§2 Тригонометричні функції числового аргументу
- •§3 Властивості тригонометричних функцій
- •§4 Основні тригонометричні тотожності
- •§5 Формули зведення
- •§6 Основні формули тригонометрії
- •§7 Властивості та графіки тригонометричних функцій Властивості і графік функції
- •Властивості і графік функції
- •Властивості і графік функції
- •Властивості та графік функції
- •§8 Обернені тригонометричні функції
- •§9 Розв’язання найпростіших тригонометричних рівнянь
- •§ 10 Розв’язання тригонометричних рівнянь
- •§ 11 Розв’язання тригонометричних нерівностей
- •Розділ 2 Похідна функції та її застосування
- •§ 12 Приріст функції в точці. Похідна функції та її механічний зміст
- •§ 13 Похідна степеневої функції
- •§14 Похідна суми, різниці, добутку та частки двох функцій Правила диференціювання
- •§15 Похідна складеної функції
- •§ 16 Похідні тригонометричних функцій
- •§ 17 Похідна показникової функції
- •§ 18 Похідна логарифмічної функції
- •§ 19 Геометричний зміст похідної
- •§ 20 Похідні вищих порядків
- •§ 21 Диференціал функції і його застосування до наближених обчислень
- •§ 22 Ознака сталості, зростання та спадання функції.
- •§ 23 Екстремум функції
- •§ 24 Побудова графіків функцій Загальна схема для побудови графіків функцій
- •§ 25 Найменше та найбільше значення функції
- •Розділ 3 Інтеграл та його застосування
- •§ 26 Первісна функції. Невизначений інтеграл та його властивості
- •Основні властивості невизначених інтегралів
- •Основні формули інтегрування
- •§ 27 Визначений інтеграл та його властивості
- •Основні властивості визначеного інтегралу:
- •§ 28 Площа криволінійної трапеції
- •§ 29 Застосування визначеного інтеграла при розв’язанні фізичних задач
- •Розділ 4 Елементи теорії ймовірностей і математичної статистики
- •§ 30 Елементи комбінаторики
Розділ 3 Інтеграл та його застосування
§ 26 Первісна функції. Невизначений інтеграл та його властивості
Функція
![]() називається первісною
для функції
називається первісною
для функції
![]() на деякому проміжку, якщо для всіх
на деякому проміжку, якщо для всіх
![]() із цього проміжку виконується рівність:
із цього проміжку виконується рівність:
![]() .
.
Якщо функція
![]() є первісною для
є первісною для
![]() на деякому проміжку, то для довільної
постійної
на деякому проміжку, то для довільної
постійної
![]() функція
функція
![]() також є первісною для функції
також є первісною для функції
![]() і будь-яка первісна для функції
і будь-яка первісна для функції
![]() на цьому проміжку має вигляд
на цьому проміжку має вигляд
![]() ,
де
,
де
![]() - довільна стала (число).
- довільна стала (число).
Сукупність усіх
первісних для функції
![]() на проміжку називають невизначеним
інтегралом цієї
функції і позначають
на проміжку називають невизначеним
інтегралом цієї
функції і позначають
![]() .
.
Таким чином:
![]() .
.
Основні властивості невизначених інтегралів
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]() ,
,
![]() ;
;
5. Якщо
![]() і
і
![]() ,
то
,
то
![]()
![]() .
.
Основні формули інтегрування
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]()
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
147. Довести,
що функція
![]() є первісною для функції
є первісною для функції
![]() на заданому проміжку:
на заданому проміжку:
1)
![]() 2)
2)
![]()
3)
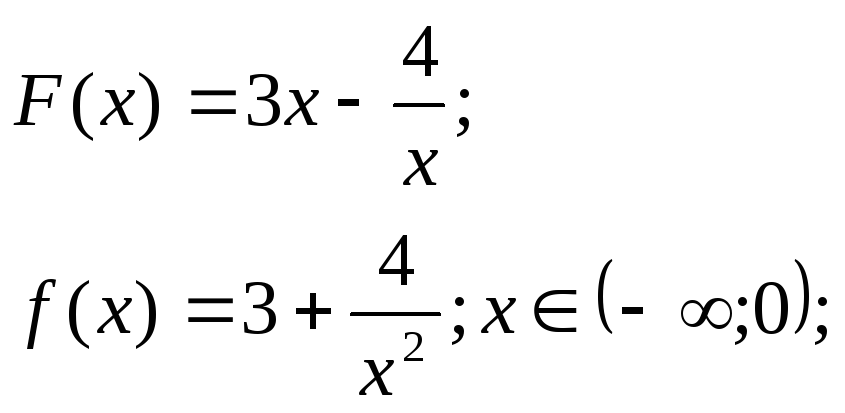 4)
4)
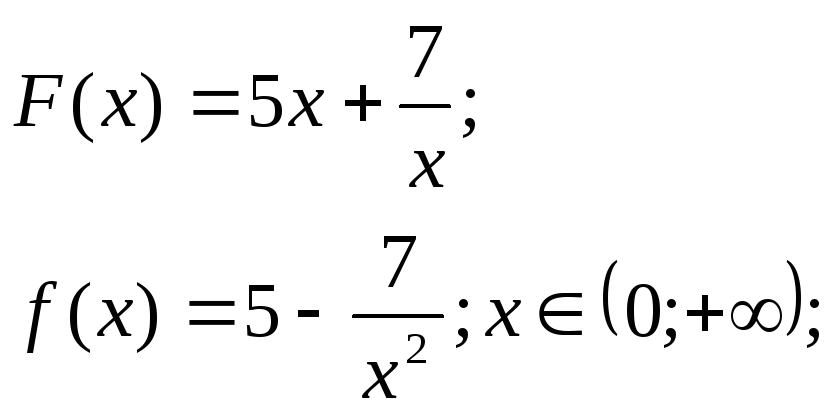
5)
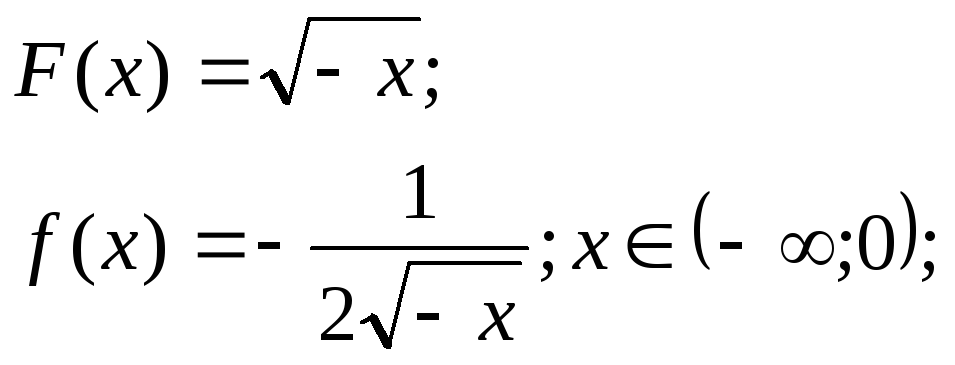 6)
6)
![]()
7)
![]() 8)
8)
![]()
9)
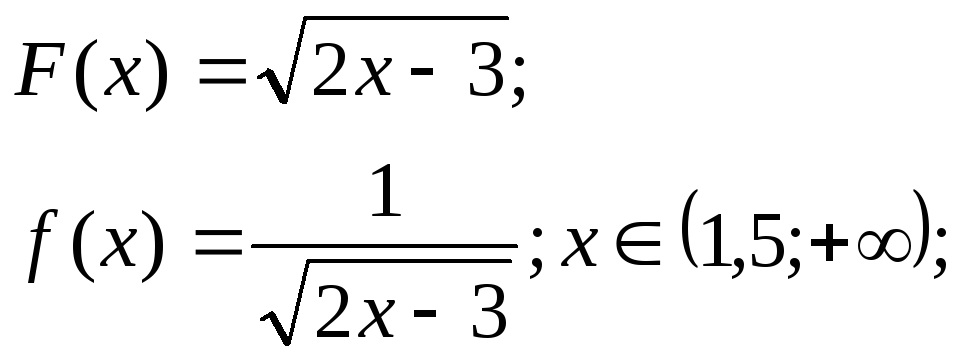 10)
10)
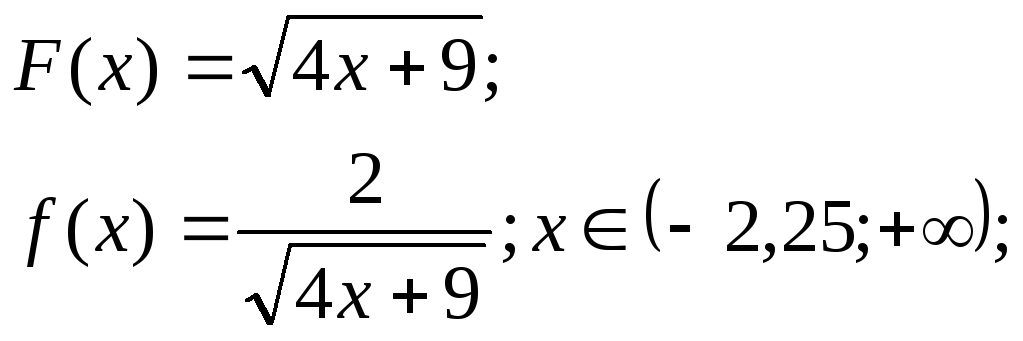
11)
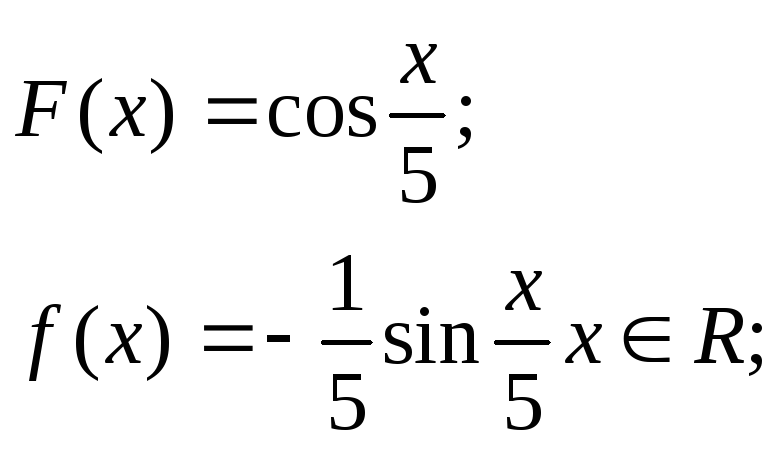 12)
12)
![]()
13)
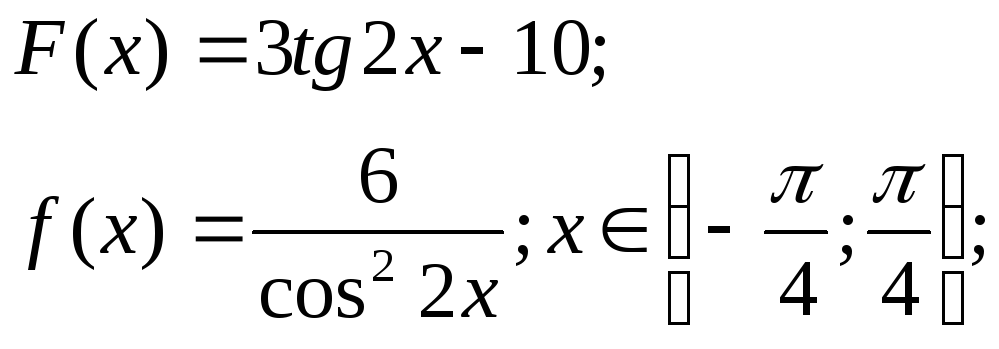 14)
14)
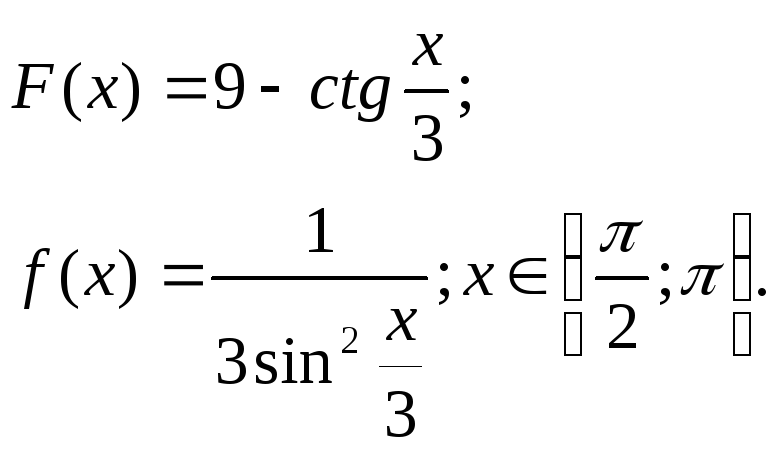
148. Знайти інтеграли:
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() ;
;
9)
![]() ; 10)
; 10)
![]() ;
;
11)
![]() ; 12)
; 12)
![]() .
.
149. Знайти інтеграли безпосередньо:
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() ;
;
9)
![]() ; 10)
; 10)
![]() ;
;
11)
![]() ; 12)
; 12)
![]() ;
;
13)
![]() ; 14)
; 14)
![]() ;
;
15)
![]() ; 16)
; 16)
![]() ;
;
17)
![]() ; 18)
; 18)
![]() ;
;
19)
![]() ; 20)
; 20)
![]() ;
;
21)
![]() ; 22)
; 22)
![]() ;
;
23)
![]() ; 24)
; 24)
![]() ;
;
25)
![]() ; 26)
; 26)
![]() ;
;
27)
![]() ; 28)
; 28)
![]() ;
;
29)
![]() ; 30)
; 30)
![]() ;
;
31)
![]() ; 32)
; 32)
![]() ;
;
33)
![]() ; 34)
; 34)
![]() ;
;
35)
![]() ; 36)
; 36)
![]() ;
;
37)
![]() ; 38)
; 38)
![]() .
.
150. Знайти невизначені інтеграли :
1)
![]() ; 2)
; 2)
![]() ;
;
3)![]() ; 4)
; 4)![]() ;
;
5)![]() ; 6)
; 6)![]() ;
;
7)![]() ; 8)
; 8)![]() ;
;
9)
![]() ; 10)
; 10)
![]() ;
;
11)
![]() ; 12)
; 12)
![]() /
/
151. Знайти невизначені інтеграли методом заміни змінної;
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() ;
;
9)
![]() ; 10)
; 10)
![]() ;
;
11)
![]() ; 12)
; 12)
![]() ;
;
13)
![]() ; 14)
; 14)
![]() ;
;
15)
![]() ; 16)
; 16)
![]() ;
;
17)
![]() ; 18)
; 18)
![]() ;
;
19)
![]() ; 20)
; 20)
![]() ;
;
21)
![]() ; 22)
; 22)
![]() ;
;
23)
![]() ; 24)
; 24)![]() ;
;
25)
![]() ; 26)
; 26)
![]() ;
;
27)
![]() ; 28)
; 28)
![]() ;
;
29)
![]() ; 30)
; 30)
![]() ;
;
31)
![]() ; 32)
; 32)
![]() .
.
§ 27 Визначений інтеграл та його властивості

Розглянемо
неперервну функцію
![]() ,
невід’ємну на відрізку
,
невід’ємну на відрізку
![]() .
Розіб’ємо відрізок
.
Розіб’ємо відрізок
![]() на
на
![]() рівних частин
рівних частин
![]() ,
довжина кожної частини дорівнює
,
довжина кожної частини дорівнює
![]() .
Утворимо суму
.
Утворимо суму
![]() добутків
добутків
![]() ,
де
,
де
![]() ,
яка називається інтегральною
сумою:
,
яка називається інтегральною
сумою:
![]() .
Знайдемо
.
Знайдемо
![]() .
Границя інтегральної суми при умові,
що кількість відрізків
.
Границя інтегральної суми при умові,
що кількість відрізків
![]() ,
називається
,
називається
визначеним
інтегралом
функції![]() на відрізку
на відрізку
![]() і позначають
і позначають
![]() Якщо
Якщо
![]() - первісна для функції
- первісна для функції
![]() на відрізку
на відрізку
![]() ,
то
,
то
![]()
Ця формула
називається формулою Ньютона – Лейбніца
і є правильною для будь-якої неперервної
на відрізку
![]() функції
функції
![]() ;
вона пов’язує поняття інтеграла і
первісної і є правилом обчислення
інтегралів.
;
вона пов’язує поняття інтеграла і
первісної і є правилом обчислення
інтегралів.
Основні властивості визначеного інтегралу:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5. Якщо
![]() ,
то
,
то
![]()
152. Обчислити інтеграли:
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() ;
;
9)
![]() ; 10)
; 10)
![]() ;
;
11)
![]() ; 12)
; 12)
![]() ;
;
13)
![]() ; 14)
; 14)
![]() ;
;
15)
![]() ; 16)
; 16)
![]() ;
;
17)
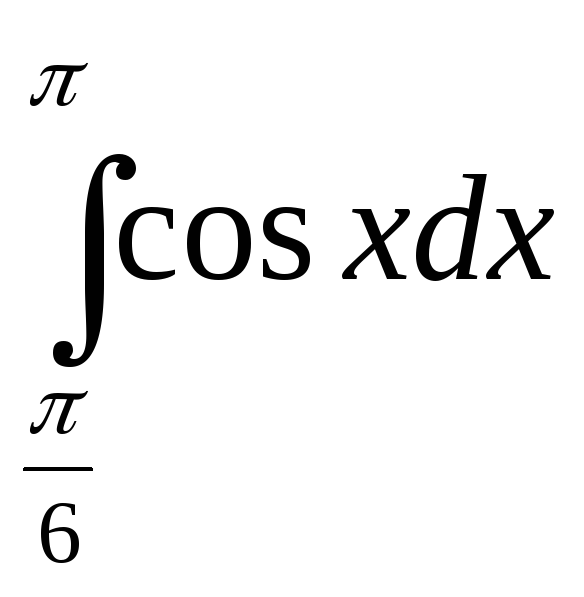 ; 18)
; 18)
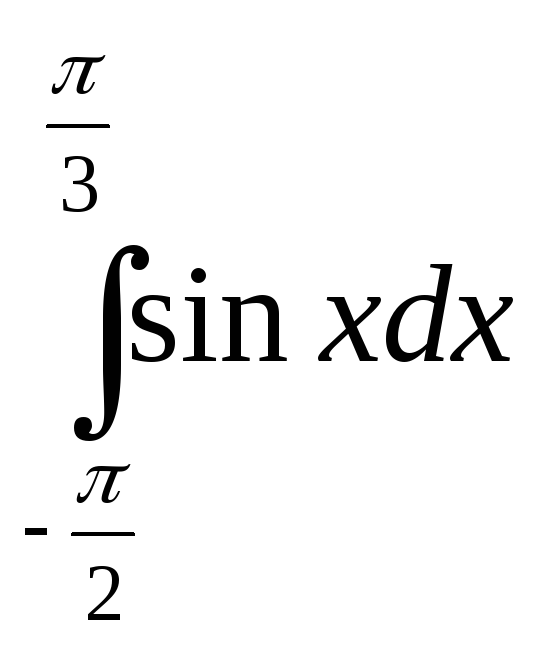 ;
;
19)
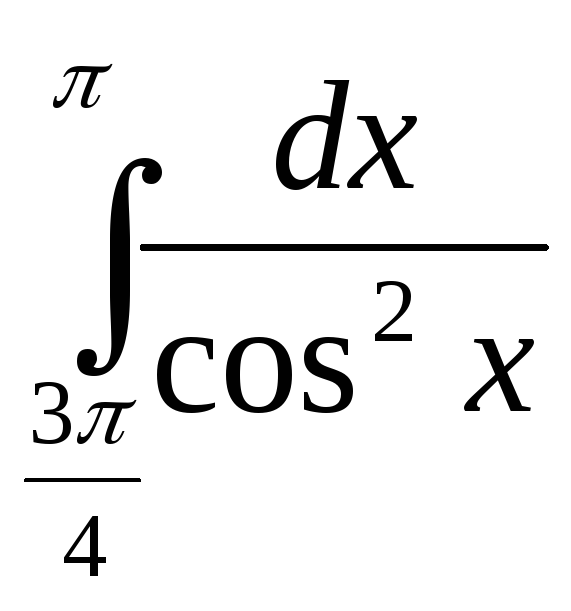 ; 20)
; 20)
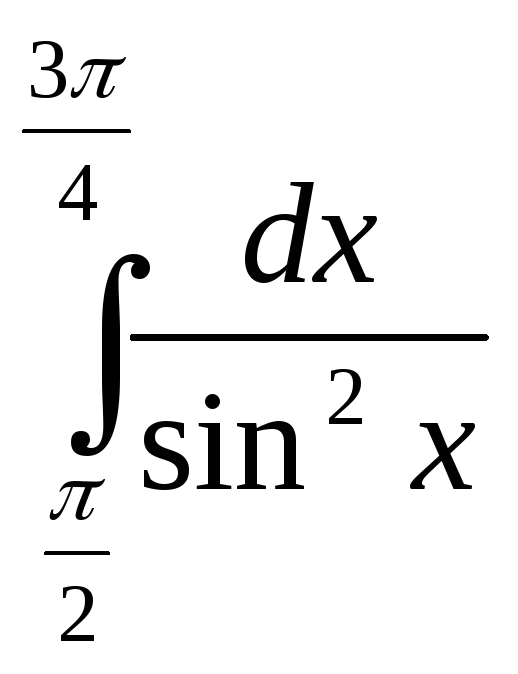 ;
;
21)
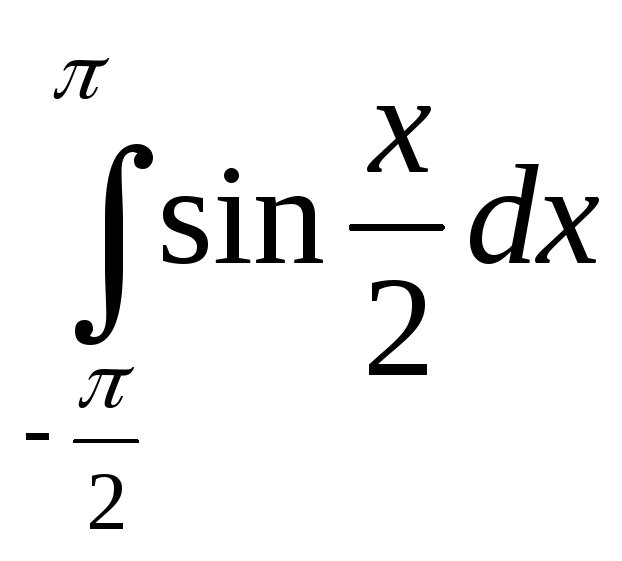 ; 22)
; 22)
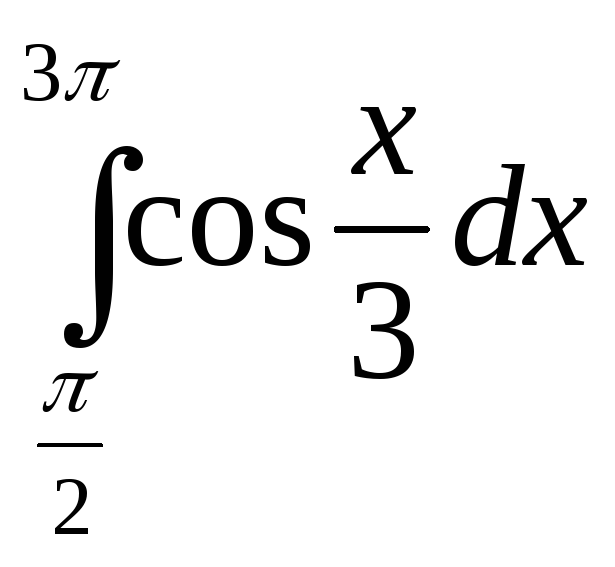 ;
;
23)
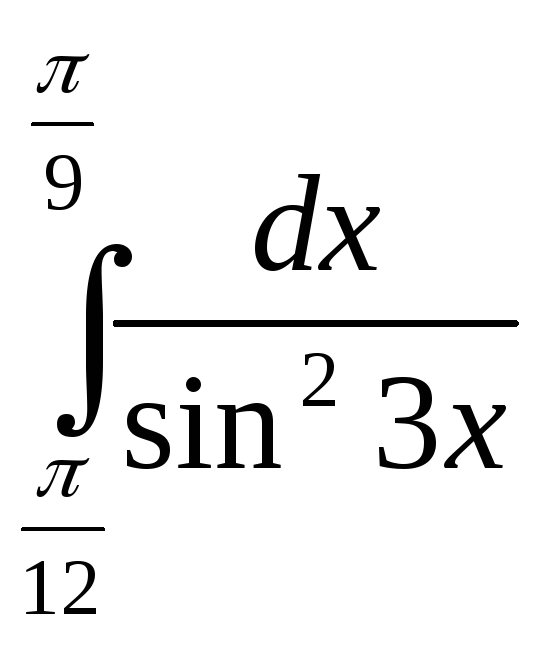 ; 24)
; 24)
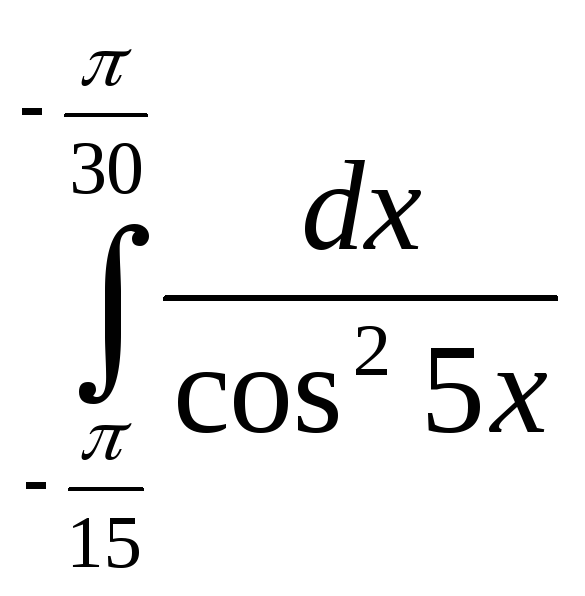 ;
;
25)
![]() ; 26)
; 26)
![]() ;
;
27)
![]() ; 28)
; 28)
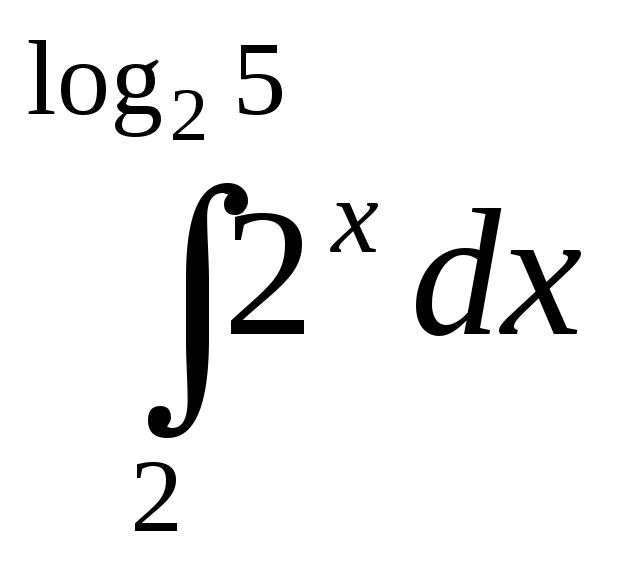 ;
;
29)
![]() ; 30)
; 30)
![]() ;
;
31)![]() ; 32)
; 32)
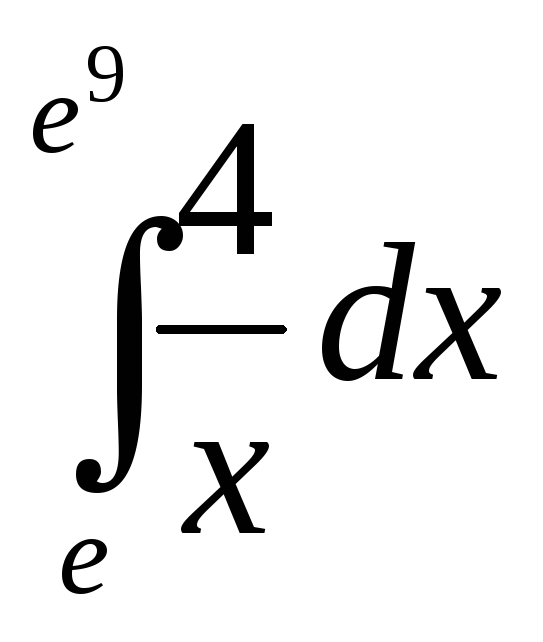 ;
;
33)
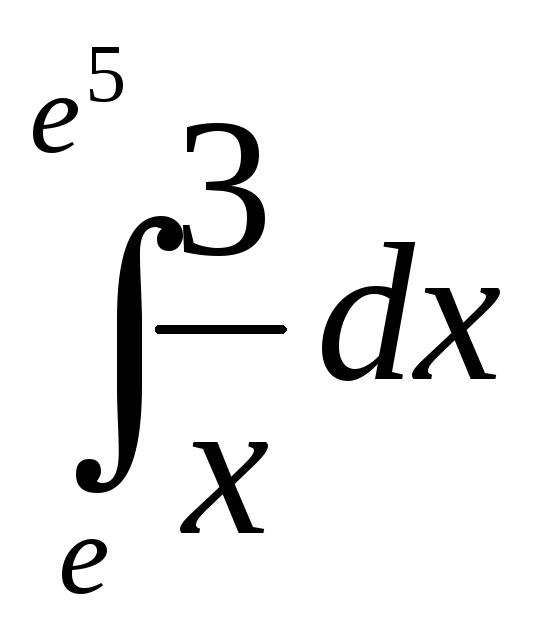 ; 34)
; 34)
![]() .
.
153. Обчислити інтеграли:
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() ;
;
9)
![]() ; 10)
; 10)
![]() ;
;
11)
![]() ; 12)
; 12)
![]() ;
;
13)
![]() ; 14)
; 14)
![]() ;
;
15)
![]() ; 16)
; 16)
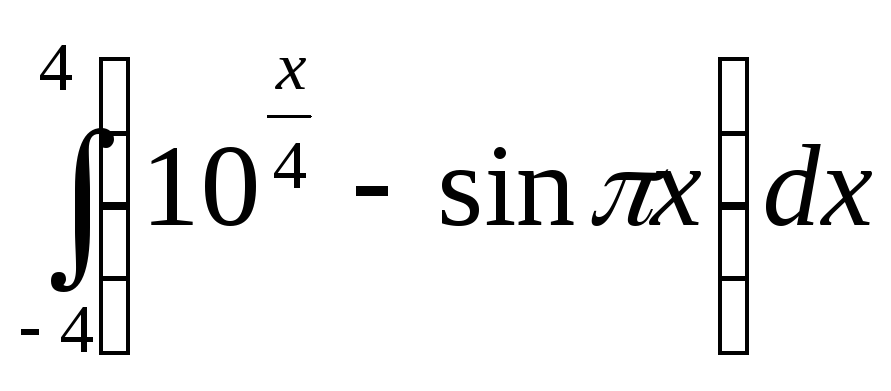 ;
;
17)
![]() ; 18)
; 18)
![]() ;
;
19)
![]() ; 20)
; 20)
![]() ;
;
21)
![]() ;
22)
;
22)
![]() ;
;
23)
![]() ; 24)
; 24)
![]() ;
;
25)
![]() ; 26)
; 26)
![]() ;
;
27)
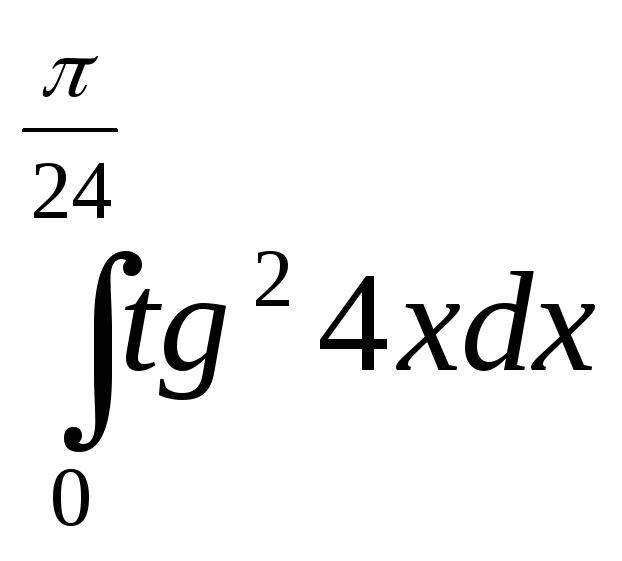 ; 28)
; 28)
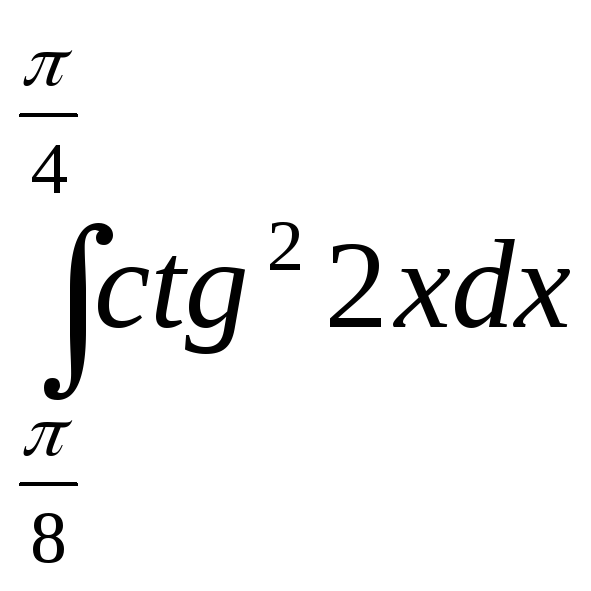 ;
;
29)
![]() ; 30)
; 30)
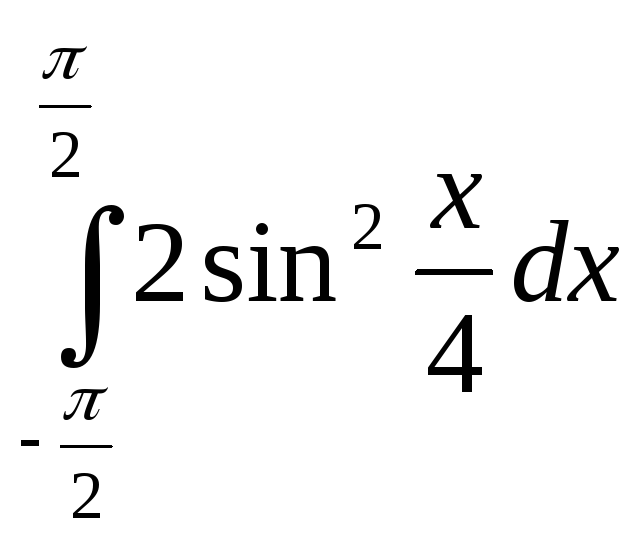 ;
;
31)
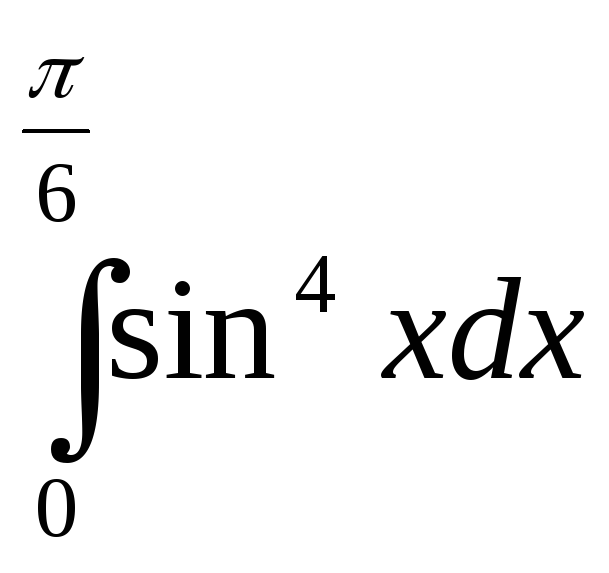 ; 32)
; 32)
![]() ;
;
33)
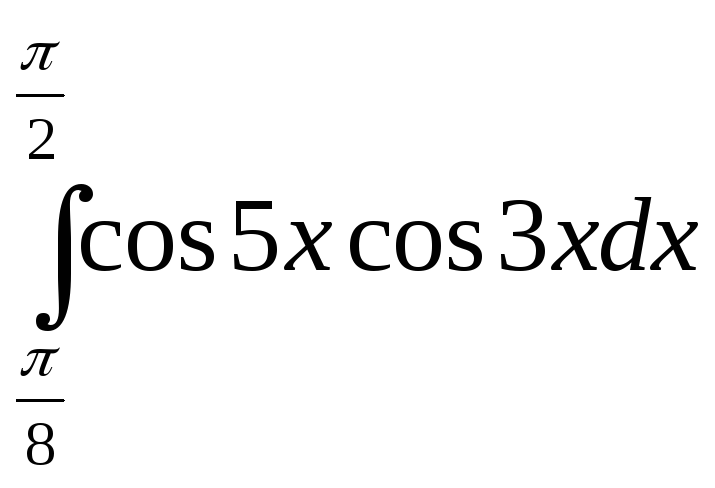 ; 34)
; 34)
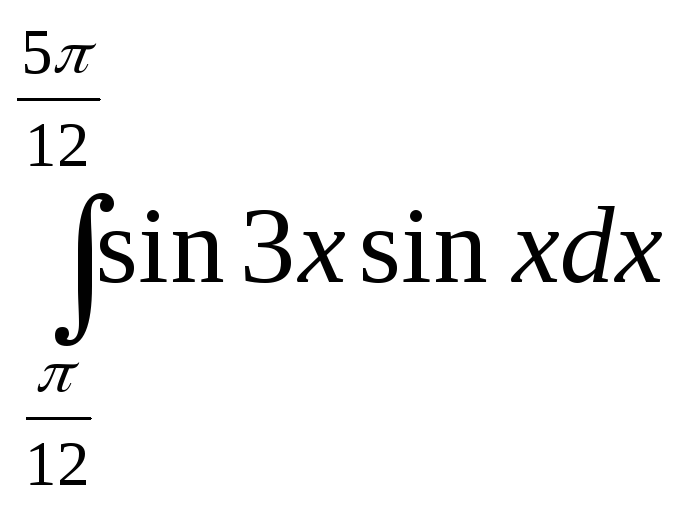 ;
;
35)
![]() ; 36)
; 36)
![]() ;
;
37)
![]() ; 38)
; 38)
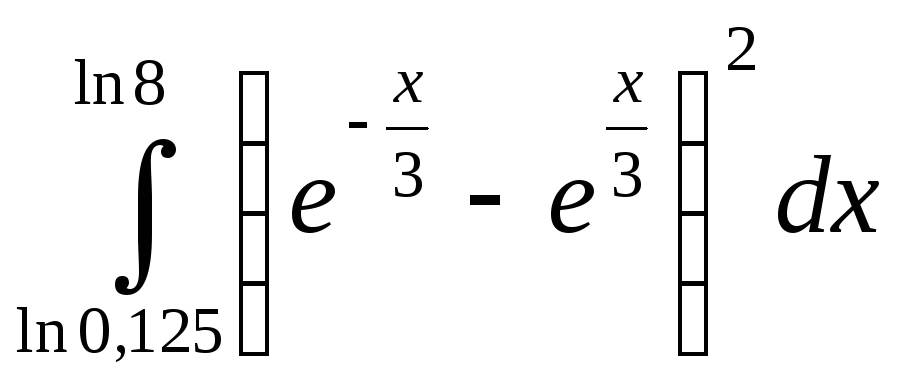 ;
;
39)
![]() ; 40)
; 40)
![]() ;
;
41)
![]() ; 42)
; 42)
![]() .
.
154. Обчислити інтеграли методом заміни змінної:
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() ; 6)
; 6)
![]() ;
;
7)
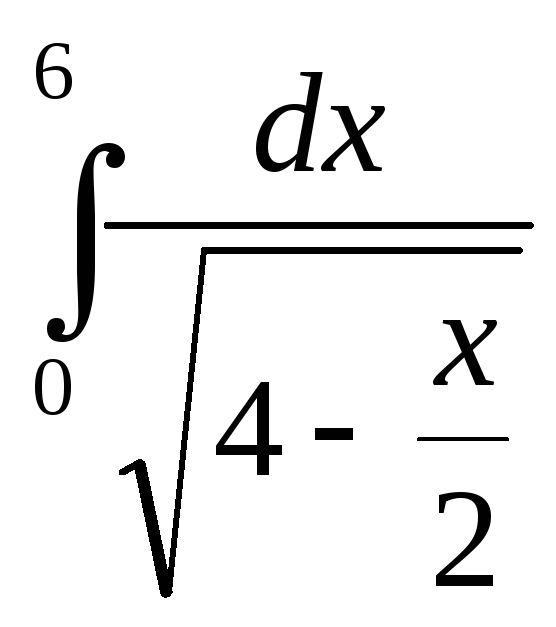 ; 8)
; 8)
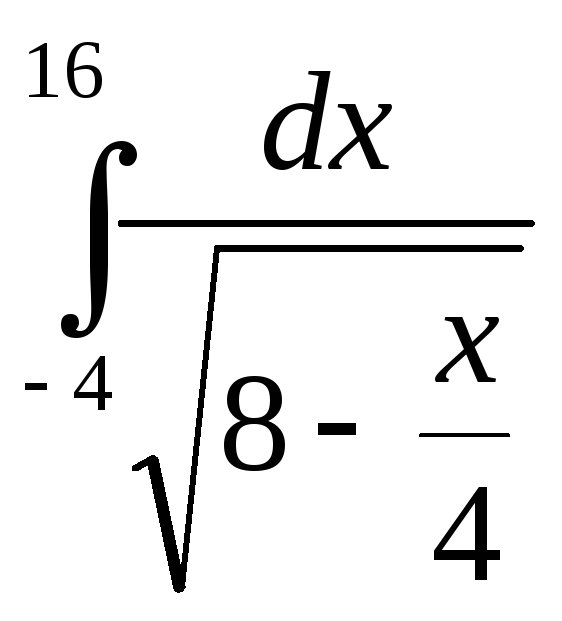 ;
;
9)
![]() ; 10)
; 10)
![]() ;
;
11)
![]() ; 12)
; 12)
![]() ;
;
13)
![]() ; 14)
; 14)
![]() ;
;
15)
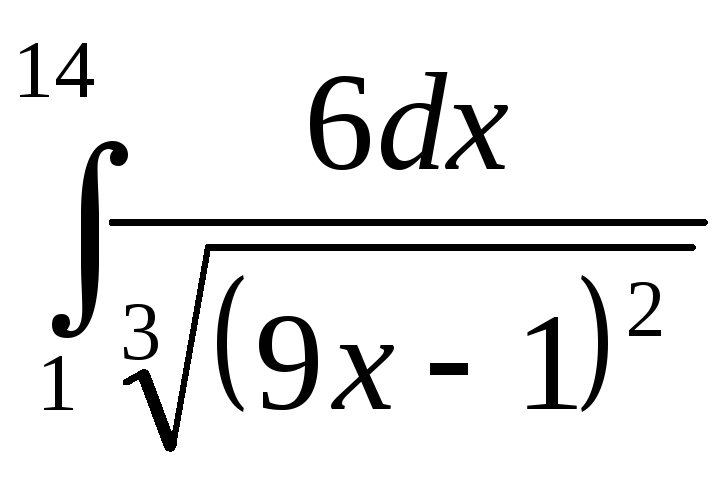 ; 16)
; 16)
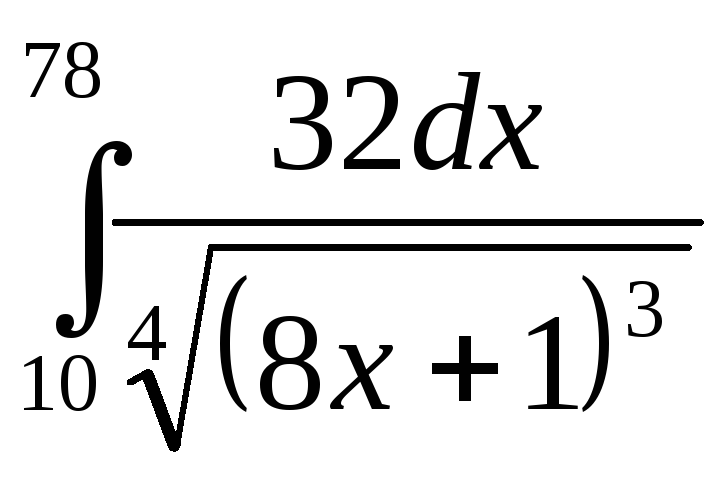 ;
;
17)
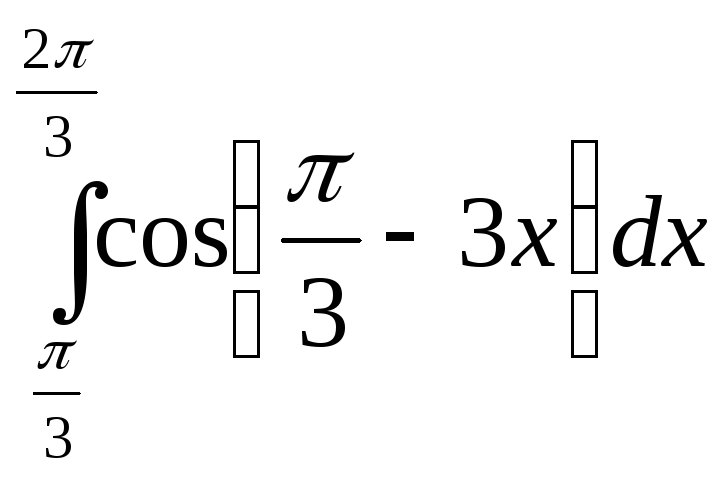 ; 18)
; 18)
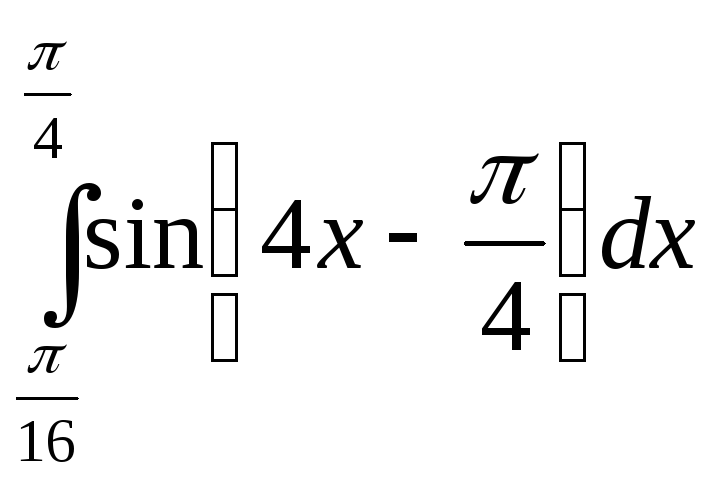 ;
;
19)
![]() ; 20)
; 20)
![]() ;
;
21)
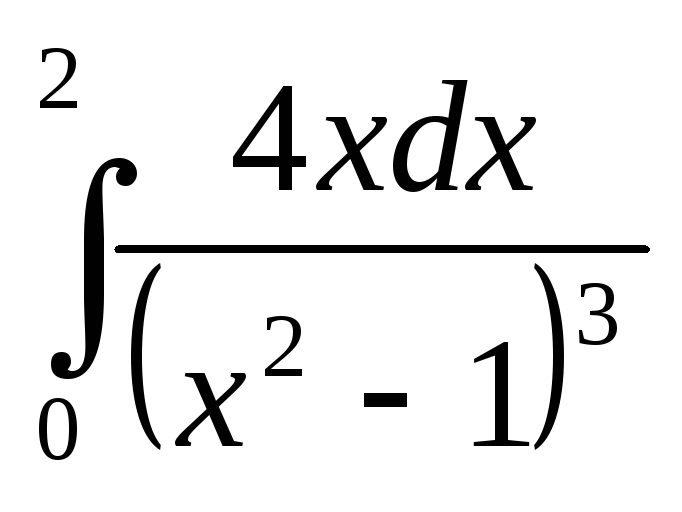 ; 22)
; 22)
![]() ;
;
23)
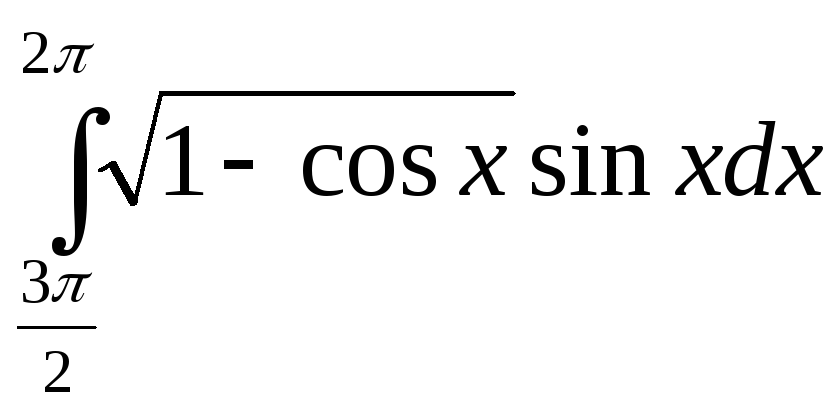 ; 24)
; 24)
![]() ;
;
25)
![]() ; 26)
; 26)
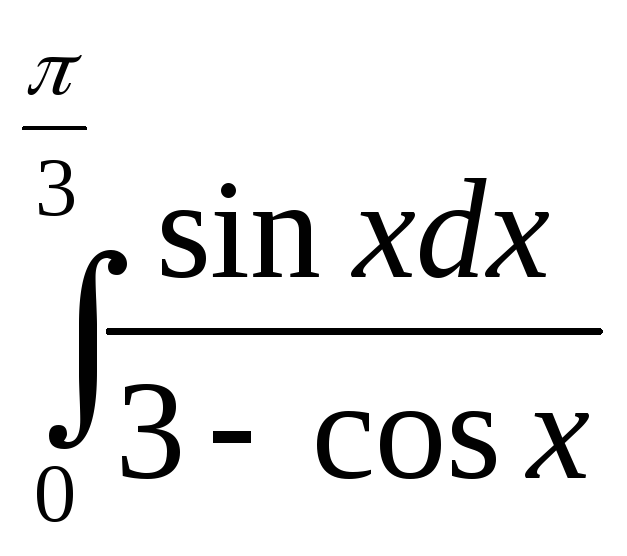 ;
;
27)
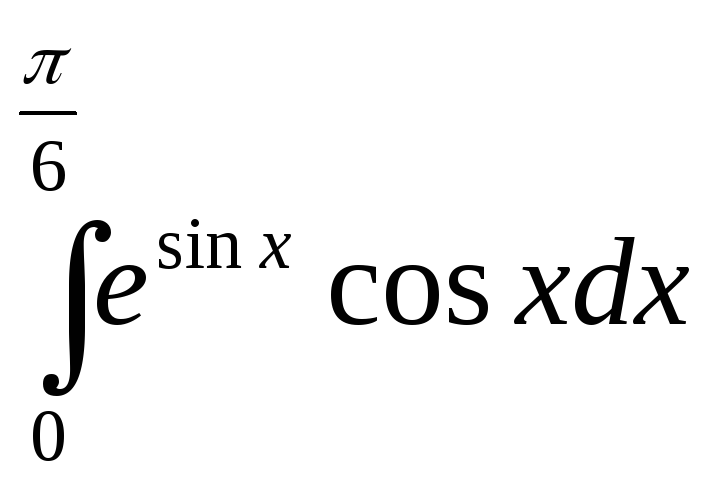 ; 28)
; 28)
![]() ;
;
29)
![]() ; 30)
; 30)
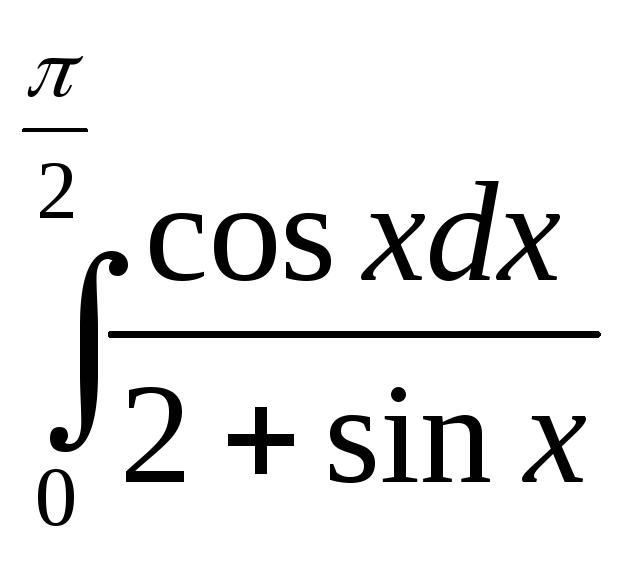 .
.
155.
Обчислити
інтеграл
![]() ,
якщо
,
якщо
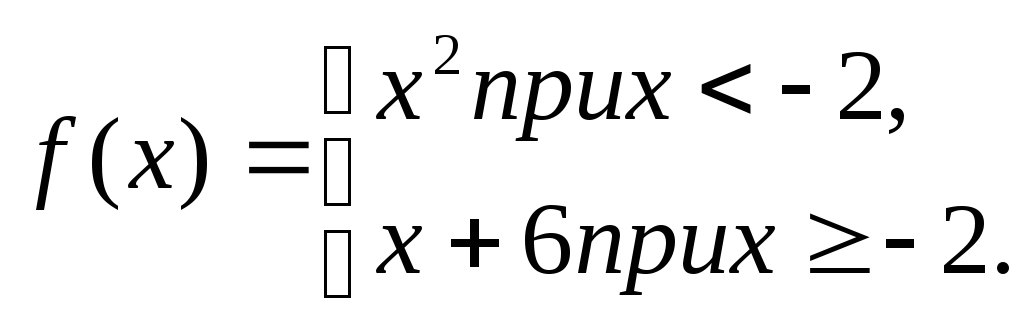
156. При
яких значеннях
![]() виконується нерівність:
виконується нерівність:
1)
![]() ; 2)
; 2)
![]() .
.
