§ 22 Ознака сталості, зростання та спадання функції.
Функція
називається зростаючою
в проміжку
,
якщо для будь-яких
і
,
що належать до цього проміжку, і таких,
що
справджується нерівність
.
Функція
називається спадною
в проміжку
,
якщо для будь-яких
і
,
що належать до цього проміжку, і таких,
що
справджується нерівність
.
Як зростаючі, так і спадні функції називаються монотонними, а проміжки, в яких функція зростає або спадає, - проміжками монотонності.
Зростання і спадання
функції
характеризується знаком її похідної:
якщо в деякому
проміжку
,
то функція зростає в цьому проміжку;
якщо ж
,
то функція спадає в цьому проміжку.
Внутрішні точки
області визначення функції
,
в яких похідна дорівнює нулю (
)
або зазнає розриву,
називаються критичними
точками.
Знаходження проміжків монотонності функції можна виконувати за таким планом:
-
Знайти область визначення заданої функції;
-
Знайти похідну
; -
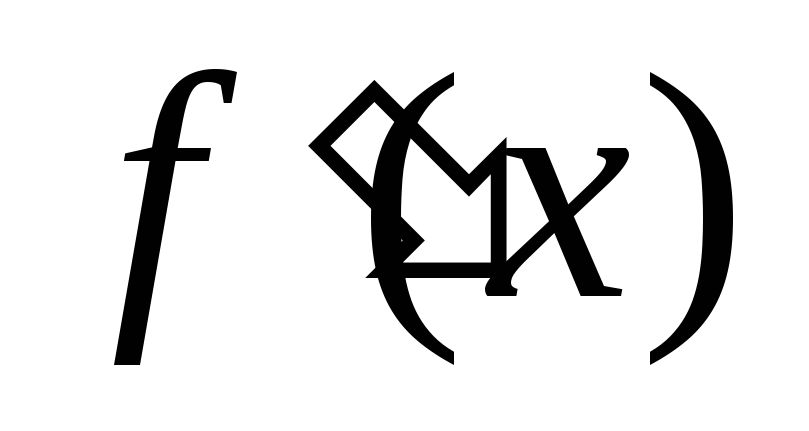Знайти критичні точки функції
; -
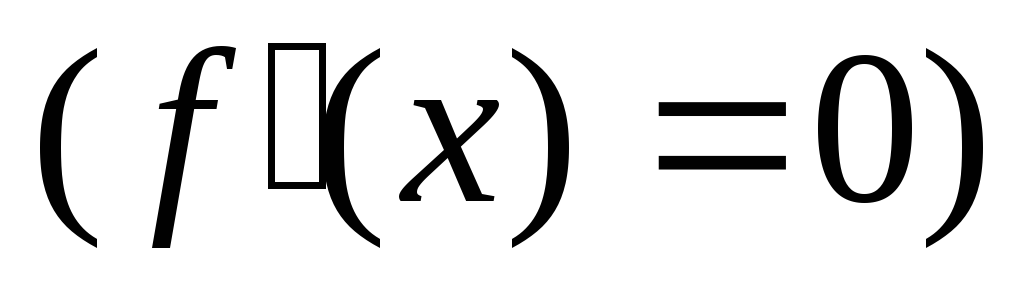Нанести критичні точки на область визначення функції;
-
Визначити знак похідної
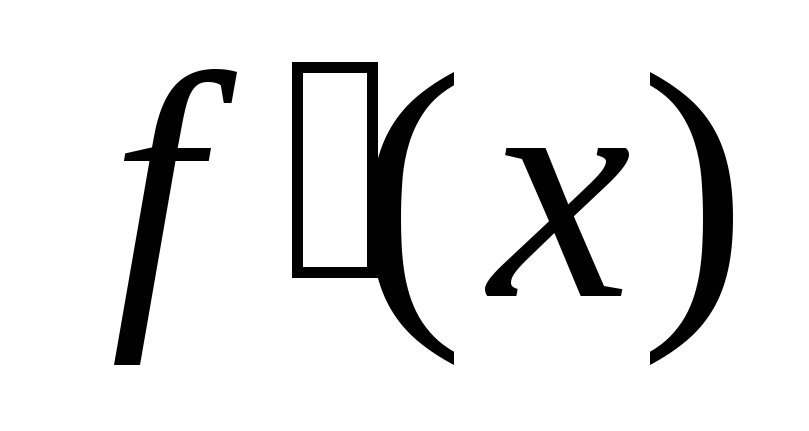на кожному з отриманих проміжків; -
Виписати проміжки монотонності функції.
125. Дослідити функції на монотонність:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
;
12)
;
13)
;
14)
;
15)
;
16)
;
17)
;
18)
;
19)
;
20)
;
21)
;
22)
;
23)
;
24)
.
126. Довести,
що функція
зростає на множині всіх дійсних чисел.
127. Довести,
що функція
спадає на проміжку
.
128. Знайти,
при яких значеннях параметра
зростає на
функція:
1)
;
2)
;
3)
;
4)
.
§ 23 Екстремум функції
Точка
з
області визначення функції
називається точкою
мінімуму
цієї функції, якщо існує такий
-
окіл
точки
,
що для всіх
з цього околу виконується нерівність
.
Точка
з
області визначення функції
називається точкою
максимуму
цієї функції, якщо існує такий
-
окіл
точки
,
що для всіх
з цього околу виконується нерівність
.
Точки мінімуму і максимуму функції називаються точками екстремуму даної функції, а значення функції в цих точках – мінімумом і максимумом (або екстремумами) функції.
Точками екстремуму
можуть бути тільки критичні точки
функції. Якщо при переході через критичну
точку
похідна
змінює
знак, то функція
має в точці
екстремум:
мінімум тоді, коли похідна змінює знак
з мінуса на плюс, і максимум, - коли з
плюса на мінус. Якщо ж при переході через
критичну точку
похідна
не змінює знака, то функція
в точці
не має екстремуму.
Правило знаходження
екстремумів функції
-
Знайти область визначення функції;
-
Знайти похідну функції
; -
Знайти критичні точки функції;
-
Нанести критичні точки на область визначення функції;
-
Визначити знак похідної
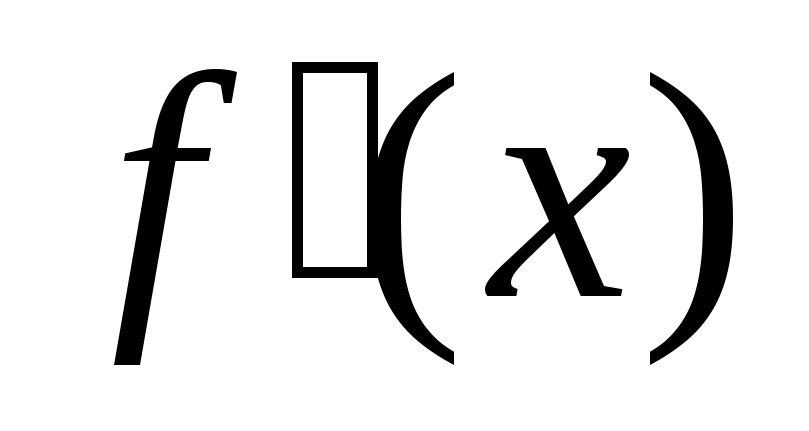на кожному з отриманих проміжків; -
Визначити наявність та характер точок екстремуму;
-
Обчислити значення функції в точках екстремуму.
129. Дослідити на екстремум такі функції:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
;
12)
;
13)
;
14)
;
15)
;
16)
;
17)
;
18)
;
19)
;
20)
.
130. Дослідити функції на монотонність та екстремум:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
;
12)
;
13)
;
14)
;
15)
;
16)
.
131. З’ясувати,
при яких значеннях параметра
функція
:
1) не має критичних точок;
2) не має екстремумів.