3.3.3. Примеры решения задач

Пример 3.3.1

Шарик массой m = 40 мг, имеющий положительный заряд q =1 нКл, движется из беcконечности со скоростью V₁ = 10 см/с. На какое минимальное расстояние r _min может приблизиться шарик к положительному точечному заряду q_{0 =} 1,33 нКл?

Дано:

m = 40 мг = 4010^-6 кг;

q = 1 нКл = 10^-9 Кл;

V₁ = 10 см/с = 0,1 м/с;

q = 1,33 нКл = 1,3310^-9Кл

______________________

r_min = ?

Анализ: На рисунке показана картина силовых линий поля, создаваемого зарядом q₀ и показан выбор и направление оси координат. Заряд q движется в отрицательном направлении оси r, и сила электрического поля совершает при этом отрицательную работу, что приводит к превращению кинетической энергии этого заряда в потенциальную энергию заряда в поле. На заряд действует только электрическая сила поля точечного заряда q₀, поэтому в этой задаче можно для решения использовать закон сохранения энергии.

Рассмотрим два положения заряда q.

Точка 1 - заряд q находится на достаточно далеком расстоянии от заряда, и потенциал ₁ в этой точке поля можно считать равным нулю и W_р1 = 0. Скорость заряда в этом случае отлична от нуля, и кинетическая энергия равна ;

Точка 2 - потенциал ₂  0 и поэтому потенциальная энергия движущегося заряда в этой точке не равна нулю W_р2 = q₂, а скорость движущегося заряда обращается в ноль, когда заряд q приблизится к заряду q₀ на минимальное расстояние, V = 0 и W_к2 = 0.

Решение: Система двух зарядов замкнутая и консервативная, поэтому можно применить закон сохранения энергии

или

Потенциал поля точечного заряда можно вычислить по формуле для воздуха  =1.

Окончательно получим

Подставляем численные значения, получим

Ответ: заряд q приблизится к другому заряду на минимальное расстояние, равное 6 см.

Пример 3.3.2

Два шарика с зарядами q₁ = 6,66 нКл и q₂ = 13,33 нКл находятся на расстоянии r₁ = 40 см друг от друга. Какую работу А надо совершить, чтобы сблизить их до расстояния r₂ = 25 см?

Д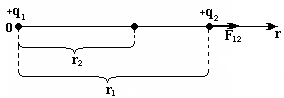ано:

q ₁ = 6,66 нКл;

q ₂ = 13,33 нКл;

r₁ = 40 см = 0,40 м;

r₂ = 25 см = 0,25 м

_______________

А₁₂ - ?

Анализ:

Для того чтобы сблизить одноименно заряженные шарики, необходимо совершить работу против сил электрического поля. Поэтому работа сил электрического поля при этом будет отрицательной, а работа внешней силы, перемещающей заряд, будет положительной.

Будем считать, что первый шарик неподвижен и создает поле, а второй перемещается в поле первого заряда.

Решение: 1 способ. Работа переменной силы находится через интеграл , где - величина перемещаемого заряда, - напряженность поля первого заряда, поскольку перемещение заряда происходит вдоль силовой линии, но в сторону обратную направлению напряженности поля, то угол будет равен .

Величина напряженности поля точечного заряда равна

,

Если в условии задачи не упоминается среда, в которой находятся заряды, то по умолчанию считается, что среда – воздух и .

Получили интеграл, взяв который, получим формулу для вычисления работы:

,

или окончательно получим

.

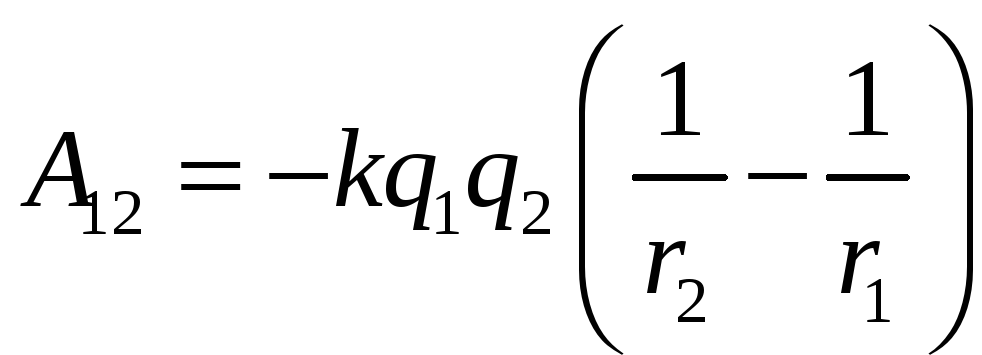2 способ. При таком методе решения задачи мы воспользуемся теоремой о потенциальной энергии. Электростатические поля – потенциальные поля, поэтому работа сил поля по перемещению заряда равна убыли потенциальной энергии перемещаемого заряда. Тогда , где ₁ и _2- - потенциалы электростатического поля, созданного первым шариком на расстояниях r₁ и r₂ от него. В этом случае мы воспользуемся уже выведенной формулой для вычисления потенциала. Потенциал поля точечного заряда q₁ в точках на расстояниях r₁ и r₂ равен

и .

Тогда

Работа же внешних сил А = -А_эл = 1,210^-6 Дж.

Ответ: для того чтобы сблизить указанные заряженные шарики, необходимо внешним силам совершить работу А = 1,210^-6 Дж. Оба способа решения задачи дают одинаковый ответ.

Пример 3.3.3

Электрическое поле образовано положительно заряженной бесконечно длинной нитью с линейной плотностью заряда  = 0,2 мк Кл/м. Какую скорость V будет иметь покоящийся электрон, если он под действием сил поля, приблизится к нити с расстояния r₁ = 1 см до расстояния r₂ = 0,5 см.

Дано:

 = 0,2 мк Кл/м = 210^-7 Кл/м ;

r₁ = 1 см = 0,01 м;

r₂ = 0,5 см = 510^-3 м;

m_e = 9,110^-31 кг;

V_{0 =} 0

_е_=1,610^-19Кл_

___________

V - ?

Анализ и решение: На рисунке показаны силовые линии поля нити в плоскости, перпендикулярной самой нити, и радиальная ось.

Для описания поведения заряженной частицы в электростатическом поле можно применить закон сохранения энергии, т.к. система замкнута и консервативна.

При движении отрицательной частицы силы поля будут совершать положительную работу, и это приведет к тому, что потенциальная энергия заряда будет убывать, а кинетическая возрастать.

В первой точке электрон имеет только потенциальную энергию, поскольку в начальный момент он покоился,

W_к1 = 0, W _п1 = e_1.

Во второй точке у заряда будет и потенциальная и кинетическая энергия

W _п2 = e₂.

По закону сохранения энергии

W_к1 + W_п1 = W_к2 + W_п2

или

;

Для нахождения (₂ - ₁) воспользуемся формулой, связывающей E с потенциалом . Для случая радиальной симметрии

или

Напряженность поля нити нам известна: , для воздуха  = 1, с учетом этого, получаем

Проинтегрируем это уравнение по координате r

вынесем постоянные множители из-под интеграла и получим

Используя табличные интегралы, получим

,

или

Подставляя полученное уравнение в выражение закона сохранения энергии, получим

-

отсюда

Подставляя численные значения, получаем

Ответ: электрон приобретет скорость, равную V = 2,9710⁷ м/с.

Пример 3.1 Две длинные одноимённо заряженные нити расположены на расстоянии r₁= 10см друг от друга. Линейные плотности зарядов одинаковы и равны ==10мкКл/м.

Какую работу А на единицу длины нити надо совершить, чтобы раздвинуть нити до расстояния = 20см ?

Анализ :

Дано:
r		=10см =20см =10мкКл/м
r2
=
a		=10см
1) E-? 2) A-?

Электростатические поля, создаваемые различными распределениями зарядов, по принципу суперпозиции складываются в каждой точке пространства. Учитывая симметрию задачи, сделаем рисунок, расположив нити перпендикулярно плоскости чертежа. Точка А удалена от обеих нитей на расстояние а = r₁. Получили равносторонний треугольник. Для того, чтобы найти направление вектора напряжённости поля, создаваемого в точке А зарядом каждой нити, поместим в эту точку пробный заряд «+1» и определим, как поля нитей действуют на этот заряд. Так как нити заряжены положительно, то они будут отталкивать пробный заряд и вектора и будут направлены так, как показано на рисунке. Вектор напряжённости суммарного поля, согласно принципу суперпозиции, находится по правилу параллелограмма.

Сила взаимодействия этих заряженных нитей зависит от расстояния между ними, поэтому работу сил электростатического поля при раздвижении нитей надо вычислять через интеграл.

Решение:

1) Из рисунка видно, что направлен вправо, и модуль его можно найти как:

т.к. и , где k=.

Окончательно получаем

.

2) Сила взаимодействия заряженных нитей зависит от расстояния между ними. Каждая нить создаёт поле, и это поле действует на заряд другой нити. - напряженность поля первой нити.

-сила, действующая на единицу длины второй нити равна:

Работу этой силы можно вычислить как:

.

Возьмём интеграл от этой функции. Все постоянные величины выносим за знак интеграла и получаем табличный интеграл, который равняется натуральному логарифму аргумента.

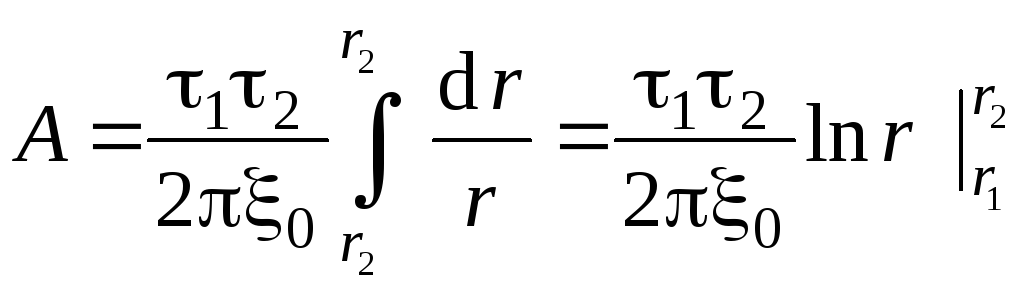
Подставим пределы интегрирования и окончательно получаем:

.

Используя данные задачи, получим численный ответ

Ответ: 1) 2)

Пример 3.3.4.

На отрезке прямого повода длиной распределен заряд с линейной плотностью

τ = 10³ нКл/м. Определите работу сил поля А по перемещению заряда q = 1нКл из точки 1 в точку 2 (см. рис.).

Дано:

τ = 10³ нКл/м

q = 1нКл

Найти:

А = ?

Анализ: Задачу можно, как рассматривалось выше, решать двумя способами. Мы выберем в этом случае второй способ решения, т.е. воспользуемся теоремой о потенциальной энергии. Работа сил электрического поля равна убыли потенциальной энергии переносимого заряда. Для того, чтобы воспользоваться этой теоремой, первым действием получим формулу для вычисления потенциала поля стержня в точках, лежащих на оси стержня, а затем вычислим работу сил поля по перемещению заряда. Поскольку в условии задачи не указана среда, в которой находятся заряды, то считается, что среда вакуум или воздух, т.е. .

Решение: На рисунке показан стержень; ось координат расположена вдоль стержня и начало координат связано с одним из концов стержня. Выделим на стержне бесконечно малый элемент длины dx, заряд на котором можно считать точечным dq = τ dx. Для определения потенциала создаваемого отрезком прямого тонкого стержня длинной , в точке с координатой , лежащей на продолжении оси этого стержня, воспользуемся принципом суперпозиции для потенциала. В случае непрерывного распределения заряда надо проинтегрировать уравнение

,

которое определяет потенциал поля, создаваемого зарядом dq, в точке с координатой х. Если перемещать элементарный заряд dq по всей длине стержня и суммировать потенциал в точке с координатой х, то придем к интегралу

.

Взяв его, получим формулу для вычисления потенциала поля заряженного стержня в токах, лежащих на оси стержня

.

Для определения работы сил поля по перемещению заряда q из положения 1 с координатой в положение 2 с координатой , воспользуемся теоремой о потенциальной энергии

.

В нашем случае , координата конечного положения заряда, равна, а , координата начального положения заряда, равна . С учетом этого, получаем выражение для вычисления разности потенциалов

.

Применим теорему о потенциальной энергии, подставив в нее полученное выражение для вычисления разности потенциалов,

Окончательно получаем

.

Подставим численные значения величин и получим численное значение искомой величины:

.

Ответ: Работа сил электростатического поля положительная и равная .