Число 3 вычитают потому, что для нормального распределения погрешностей

. Выражение называется контрэксцессом.

Оценки истинного значения на основании ограниченного ряда наблюдений.

При бесконечном числе испытаний случайная величина может принимать любые значения, называемые генеральной совокупностью. Число n этих значений называют выборкой объема n. Определяя по данным этой выборки характеристики закона распределения, получаем не истинные значения моментов, а лишь их оценки, случайно отклоняющиеся от истинных значений.

А – действительное значение искомой величины.

– оценка искомой величины.

– функция, зависящая от вида распределения и результатов измерений.

= f(x₁, x₂,…x_n). Споcобы нахождения статистических оценок зависят от законов распределения.

Требования к оценкам случайной величины.

1. С

   остоятельность – такой считается оценка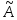 параметра А, если при увеличении числа наблюдений она стремится к истинному значению оцениваемой величины, т.е. при .

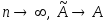2. Несмещенность – такой считается оценка 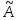, математическое ожидание которой равно истинному значению оцениваемой величины.

3. Эффективность – такая оценка 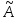, из нескольких возможных несмещенных, для которых оценка дисперсии будет минимальная. При ограниченном ряде наблюдений среднее арифметическое является несмещенной оценкой истинного значения, а также эффективной оценкой.

Интервальные оценки истинного значения.

Интервальная оценка – это более полный и надежный способ оценки случайной величины, который с заданной степенью достоверности включает в себя значения оцениваемого параметра. Здесь определяется доверительный интервал (), между границами которого с определенной доверительной вероятностью Р находится истинное значение.

Доверительная вероятность определяет область допустимых значений, а уровень значимости – критическую область. Обычно уровень значимости .

Доверительные интервалы некоторых выборочных распределений.

1. Доверительный интервал для выборочного среднего арифметического значения измеряемой величины 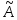при известной дисперсии .

а) Случайная величина Х (результат наблюдения) имеет нормальное распределение с параметрами m_X и Выборочное распределение оценки среднего значения , также нормально распределено и имеет те же мат. ожидание и дисперсию.

Если границы доверительного интервала , то доверительный интервал , где Z – квантиль нормированного распределения Лапласа. Результат измерения: =.

б) Случайная величина Х распределена по закону, отличному от нормального.

При возрастании объема выборки n выборочное распределение среднего значения выборки стремится к нормальному распределению независимо от вида распределения исходной величины.

2. Доверительный интервал для выборочного среднего значения измеряемой величины при неизвестной дисперсии.

Результаты Х – распределены по нормальному закону со средним значением m_X. Дисперсия неизвестна.

Выборочное распределение среднего значения имеет распределение Стьюдента:

Доверительный интервал определяется через квантиль Стьюдента в заданном интервале, а результат записывается в виде:

3. Доверительный интервал для выборочной дисперсии и среднего квадратичного отклонения результатов наблюдений.

Случайная величина Х – распределена по нормальному закону со средним значением m_X и дисперсией

Дисперсия выборки объема n независимых значений случайной величины Х.

– распределение Пирсона с k степенями свободы. .