1.5. Вектор электрического смещения

Вектор называют электрическим смещением или электростатической индукцией. Подставим значения из выражения (1.3), получаем

(1.8)

Безразмерная величина называется относительной диэлектрической проницаемостью среды и характеризует электрические свойства диэлектрика. Для всех диэлектриков , поэтому . Для вакуума и , поэтому Таким образом, относительная диэлектрическая проницаемость среды показывает, во сколько раз поле в этой среде меньше, чем в вакууме.

Теорема Гаусса для вектора :

- поток вектора электрического смещения через замкнутую поверхность равен алгебраической сумме сторонних зарядов, заключенных внутри этой поверхности.

Для графического представления электрического поля в диэлектрике неудобно пользоваться силовыми линиями (линиями напряженности), так как дивергенция вектора напряженности при наличии диэлектриков может быть отличной от нуля не только в точках расположения сторонних, но и в точках расположения связанных зарядов, плотность которых в свою очередь зависит от напряженности поля, неоднородностей среды, и т.д. Поэтому для графического изображения поля в диэлектрике пользуются линиями электрического смещения, т.е. линиями вектора . Вектор в каждой точке пространства (за исключением анизотропных сред) параллелен вектору , поэтому каждая линия смещения является вместе с тем и силовой линией. Линии смещения, так же как и силовые линии электростатического поля, не могут быть замкнутыми. Они начинаются или заканчиваются только на зарядах, или уходят в бесконечность. Однако, если строить линии поля так, чтобы густота линий, пересекающих площадку , была пропорциональна потоку вектора поля через эту площадку, то густота линий смещения и силовых линий будут меняться различным образом от одного участка пространства к другому. Некоторые силовые линии будут обрываться на связанных отрицательных зарядах диэлектрика и начинаться на положительных, тогда как соответствующие линии смещения будут проходить через и за эти заряды до встречи со сторонними зарядами. Из выражения (1.8) видно, что линии смещения могут начинаться и заканчиваться только на сторонних (свободных) зарядах, либо уходить в бесконечность. В вакууме , и линии смещения совпадают с силовыми линиями.

1.8. Условия на границе двух диэлектриков

рисунок 6

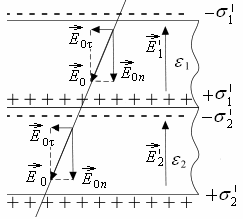
Можно показать, что линии смещения при переходе через границу диэлектриков не претерпевают разрыва. Поместим в однородное поле две сложенные вместе плоскопараллельные пластины из разных диэлектриков (рисунок 6). Сторонних зарядов на границе раздела нет. Возникшие на поверхностях пластин связанные заряды создают внутри каждой пластины перпендикулярное к ее поверхностям поле . В первой пластине напряженность этого поля равна , во второй . В сумме с нормальной составляющей напряженности поля свободных зарядов вектор дает нормальную составляющую результирующего поля в пластинах. Векторы и коллинеарны, поэтому нормальные составляющие вектора напряженности в диэлектриках соответственно равны:

(1.9)

В направлении касательной к поверхности раздела никакого дополнительного поля не создается, поэтому тангенциальная составляющая вектора при переходе через границу не меняется:

. (1.10)

Поверхностная плотность связанных зарядов, как следует из выражения (1.10), определяется нормальной составляющей результирующего поля в данной пластине:

.

Подставив и в формулу (1.2.15), имеем

(1.11)

Из выражений (1.10) и (1.11) следует, что при переходе через границу раздела двух диэлектриков нормальная составляющая напряженности поля изменяется скачком (терпит разрыв), а тангенциальная составляющая остается без изменений.

Умножим выражения (1.10) и (1.11) на и соответственно, получаем

(1.12)

Из формул (1.12) видно, что при переходе через границу раздела диэлектриков тангенциальная составляющая вектора меняется качком, а нормальная составляющая остается без изменений:

(1.13)

рисунок 7

Это равенство указывает на непрерывность линий смещения. Действительно, количество линий электрического смещения, пронизывающих площадку , равно , следовательно, к площадке, расположенной на границе раздела диэлектриков, приходит из первого диэлектрика количество линий . От этой же площадки уходит во второй диэлектрик количество линий . Так как , то и . Таким образом, линии электрического смещения не заканчиваются и не начинаются на границе раздела, т.е. проходят через нее, не претерпевая разрыва при условии, что на границе раздела нет сторонних зарядов.

Условие (19) справедливо и для границы диэлектрик-вакуум.

На границе раздела диэлектриков линии вектора терпят излом (преломляются, рисунок 8), и угол между нормалью к поверхности раздела и линией изменяется:

получаем закон преломления линий электрического смещения:

.

При переходе в диэлектрик с меньшей диэлектрической проницаемостью ε угол уменьшается.