§ 14. Понятие о многомерном распределении. Корреляционная матрица

Обобщая понятие двухмерной случайной величины, говорят о со­вокупности случайных величин Х₁, Х₂, ..., Х_п, которую называют п - мерным случайным вектором, а величины X_i - его случайными координатами (составляющими). Закон распределения случайного вектора задают в виде функции совместного распределения

F(x) = p (X₁ < x₁, Х₂ < х₂, ... , Х_п < х_п)

или в виде плотности

Обобщением понятия математического ожидания случайной ве­личины является понятие математического ожидания случайного вектора, определенного в виде

,

а обобщением понятия дисперсии D_X случайной величины является понятие корреляционной матрицы К случайного вектора X, опре­деляемой как математическое ожидание случайной матрицы (X - М_Х)(Х - М_х)^Т, т. е. К_X = M [(X - М_Х)(Х - М_х)^Т].

Так как по определению математическое ожидание случайной матрицы есть матрица, составленная из математических ожиданий ее элементов, то, например, при п = 3 получаем

или

где, как и ранее, обозначено - дисперсии X_i , a K_ij = K_XiYj - корреляционные моменты Х_i и X_j . В общем случае мат­рица K имеет вид:

(1.99)

Таким образом, диагональными элементами корреляционной матрицы являются дисперсии случайных величин X_i, а недиагональ­ными - корреляционные моменты между случайными вели­чинами (при ). Так как , то корреляци­онная матрица всегда симметрична относительно главной, диагонали, т. е. .

Для независимых величин матрица K будет диагональной

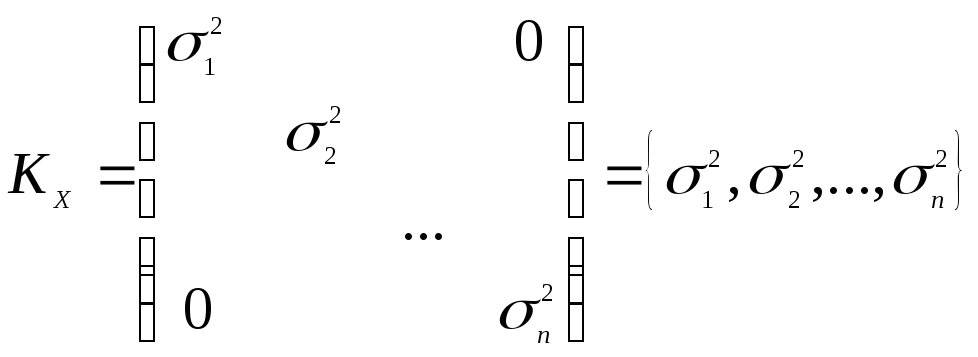(1.100)

Ее называют также дисперсионной матрицей. Если при этом все дис­персии равны между собой , то

(1.101)

где Е — единичная матрица.

Из матрицы (1.99) нетрудно составить так называемую нормиро­ванную корреляционную матрицу:

(1.102)

где r_ij - коэффициент корреляции между X_i и X_j , вычисляемый по формуле

(1.103)

Большое значение в теории обработки геодезических измерений имеет так называемый нормальный случайный вектор, плотность рас­пределения вероятностей которого (плотность совместного распре­деления X₁, X₂, ..., Х_п) имеет вид

(1.104)

где det К_X - определитель корреляционной матрицы К_X.

1.229. Из урны, в которой а белых и b черных шаров, вынимается один шар. Рассматриваются случайные величины:

Построить корреляционную и нормированную корреляционную матрицу систе­мы случайных величин.

Решение. Напишем ряд распределения для случайных величин X и Y. Очевидно, получим

xi	1	0
pxi

yi	1	0
Pyi

Далее находим математическое ожидание

Дисперсии

Аналогично

Корреляционный момент получим по формуле (1.90)

Но вероятности

Поэтому

(1.105)

Отсюда следует, что коэффициент корреляции

Корреляционная матрица

Заметим, что здесь определитель det K = 0. Такая матрица называется вырож­денной.

1.230. Могут ли быть корреляционными следующие матрицы:

Ответ: 1) да; 2) нет; 3) да; 4) да.

1.231. Написать плотность многомерного нормального распределения, если корреляционные матрицы К случайных векторов X и X имеют вид матриц K₁ и K₄ из предыдущей задачи.

1.232. Найти коэффициент корреляции r_ху , если det K = 1, a σ_x = σ_Y = 2.

Ответ: r_ху = ±0,75.

1.233. Написать нормированную корреляционную матрицу для пяти углов, измеренных способом круговых приемов. Указание (см. задачу 1.226).

Найти корреляционную матрицу, если с. к. о. измеренного направления σ = 3".