
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Факультет радиофизики и электроники
Кафедра радиофизики
Лабораторная работа изучение основных свойств и параметров цифровых фильтров Минск 2005
1. Аналоговые низкочастотные фильтры-прототипы
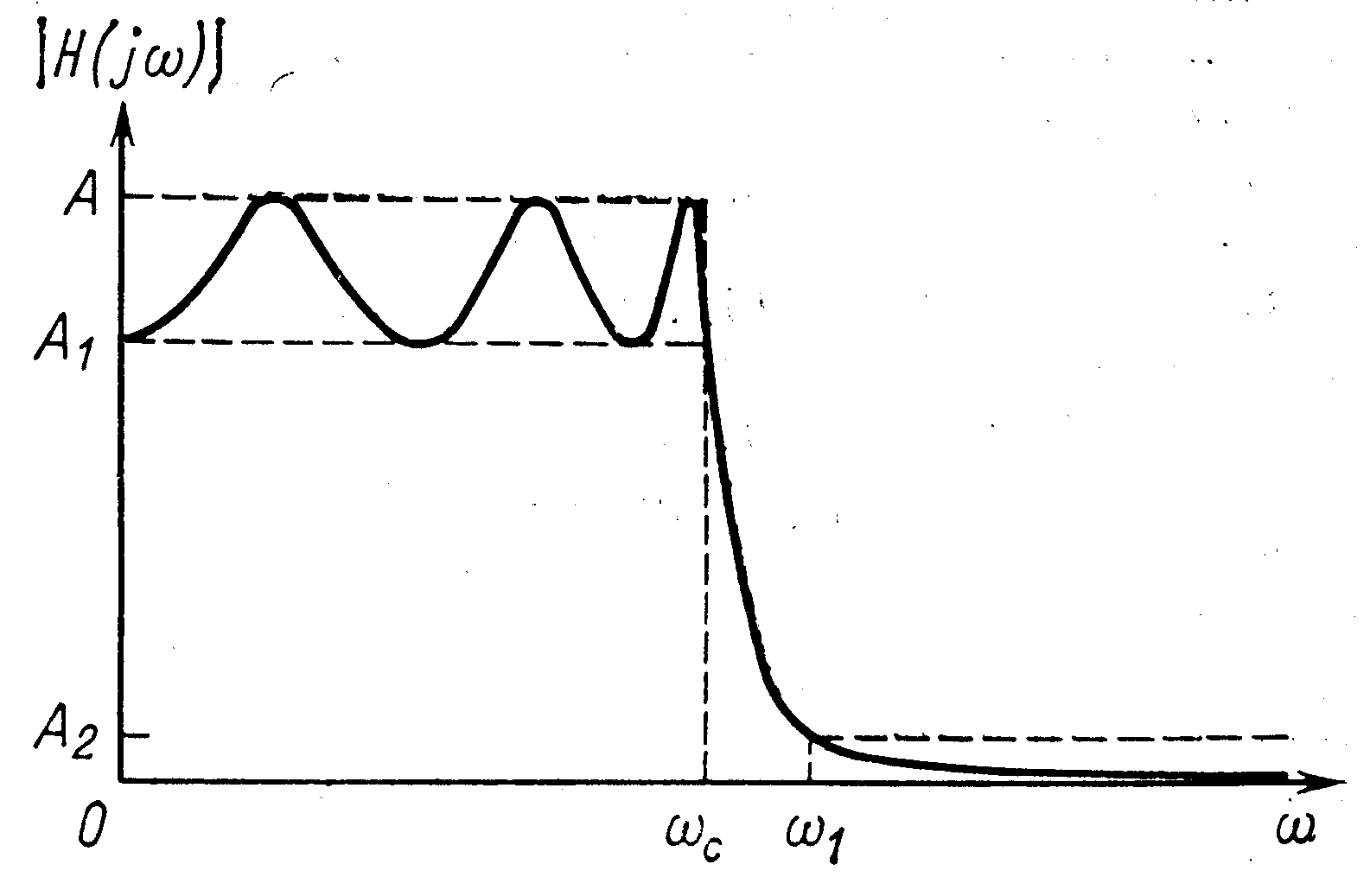
Фильтр нижних частот представляет собой устройство, которое пропускает сигналы низких частот и задерживает сигналы высоких частот. В общем случае определим полосу пропускания как интервал частот 0<<с, полосу задерживания как частоты >с, переходную область как диапазон частот с<<1 (с – частота среза). Эти частоты обозначены на рис. 1, на котором приведена реальная амплитудно-частотная характеристика фильтра нижних частот, где в данном случае заштрихованные области представляют собой допустимые отклонения характеристики в полосе пропускания и задерживания.
|
|
|
|
Рис. 1. Реальная амплитудно-частотная характеристика фильтра нижних частот. |
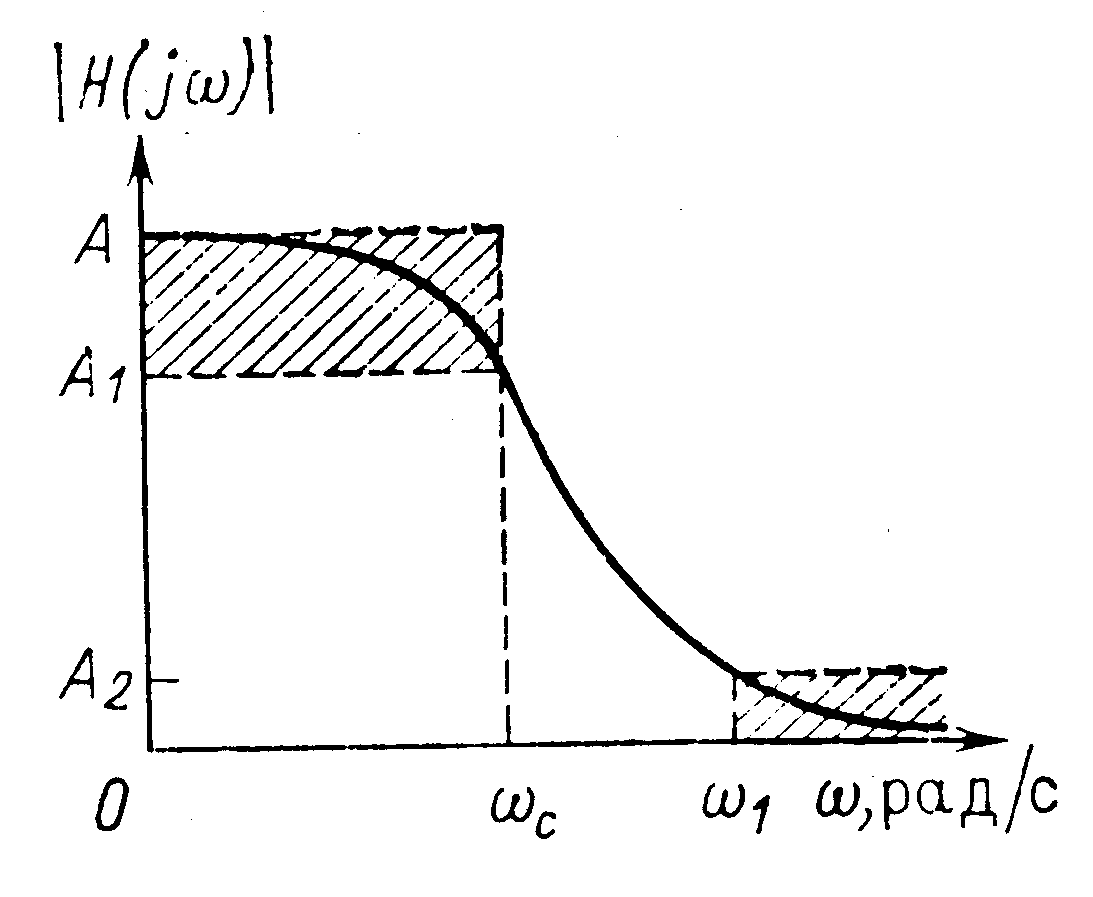
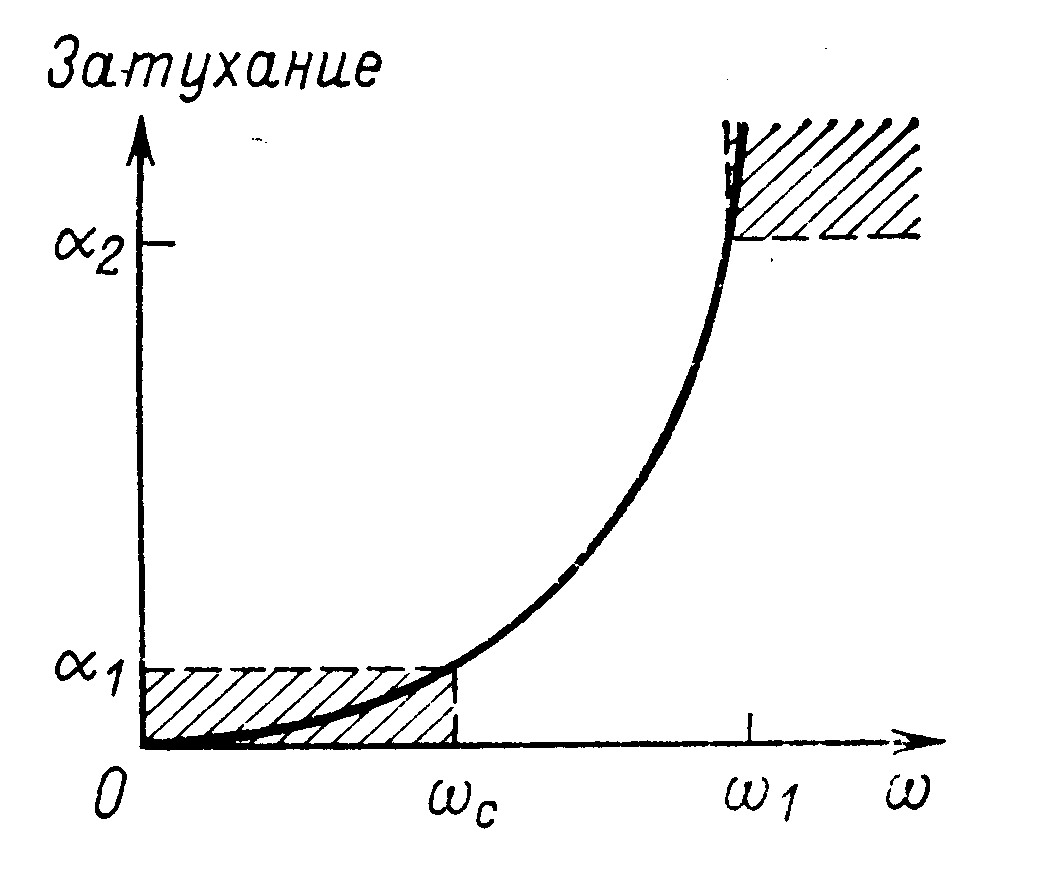
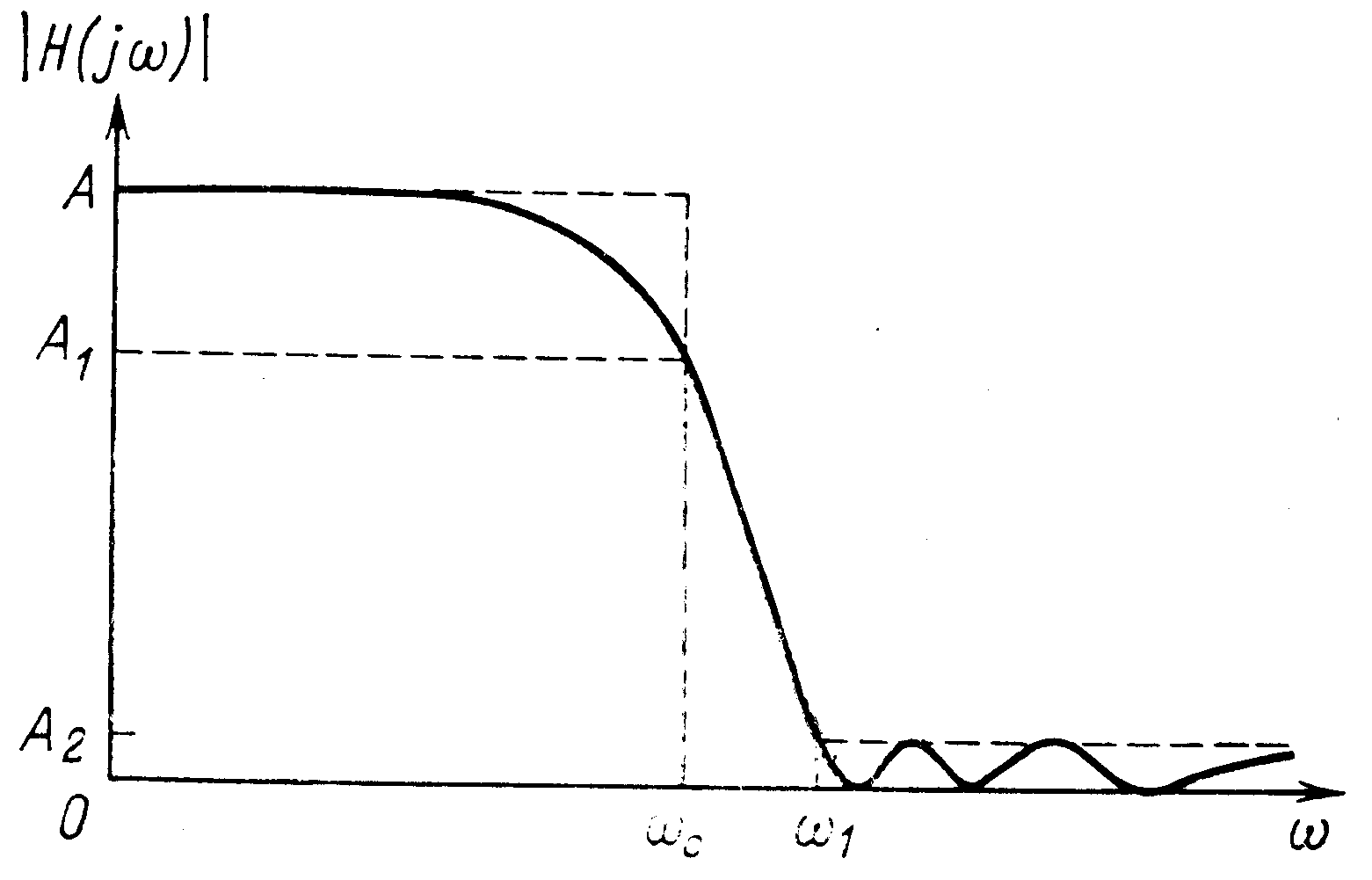
Рис 2. Логарифмическая характеристика фильтра нижних частот. |
Если минимальное затухание выбрать за нормированный уровень 0 (А=1 на рис. 1), то логарифмическая характеристика фильтра нижних частот имеет вид, изображенный на рис. 2. Максимальное затухание в децибелах в полосе пропускания составляет 1, а минимальное затухание в полосе задерживания 2 (А1 и А2 – соответственно значения амплитудно-частотной характеристики). Затухание 1 не может превышать 3 дБ, в то время как типовое значение 2 значительно больше и может находиться в пределах 202100 дБ (в этом случае имеем 0,1А20,00001).
Коэффициент усиления фильтра нижних частот представляет собой значение его передаточной функции при s=0 или, что эквивалентно, значение его амплитудно-частотной характеристики на частоте =0. Следовательно, коэффициент усиления реального фильтра с амплитудно-частотной характеристикой, показанной на риc. 1, равен А.
Существует много типов фильтров нижних частот, удовлетворяющих данному набору технических требований, таких, как А1, А2, с, 1, обозначенных на рис. 1, или 1, 2, с, 1 – на рис. 2. Фильтры Баттерворта, Чебышева, инверсные Чебышева и эллиптические образуют четыре наиболее известных класса. Фильтр Баттерворта обладает монотонной характеристикой, подобной характеристике на рис. 1 и рис. 2. (Характеристика является монотонно спадающей, если она никогда не возрастает с увеличением частоты.) Характеристика фильтра Чебышева содержит пульсации (колебания передачи) в полосе пропускания и монотонна в полосе задерживания. На рис. 3 изображен вид характеристики фильтра Чебышева шестого порядка. Инверсная характеристика фильтра Чебышева монотонна в полосе пропускания и обладает пульсациями в полосе задерживания. Пример характеристики фильтра шестого порядка приведен на рис. 4.
|
|
|
|
Рис. 3. Амплитудно-частотная характеристика фильтра Чебышева шестого порядка. |
Рис. 4. Амплитудно-частотная характеристика инверсного фильтра Чебышева шестого порядка. |
1.1. Фильтры Баттерворта
Вероятно, наиболее простая амплитудно-частотная характеристика фильтра нижних частот у фильтра Баттерворта, которая в случае n-го порядка определяется следующим образом:
|
|
|
(1) |
Эта характеристика фильтра Баттерворта монотонно спадает (никогда не возрастает) при увеличении частоты. Увеличение порядка также приводит к улучшению характеристики.
Фильтр Баттерворта представляет собой полиномиальный фильтр и в общем случае обладает передаточной функцие й вида:
|
|
|
(2) |
где К – постоянное число. Для нормированного фильтра, т. е. при с=1 рад/с, передаточную функцию можно записать в виде произведения сомножителей для n=2, 4, 6 ... как
|
|
|
(3) |
или для n=3, 5, 7, ... как
|
|
|
(4) |
Чем выше порядок фильтров, тем лучше их амплитудно-частотная характеристика. Однако более высокий порядок усложняет схемную реализацию и вследствие этого повышает стоимость. Таким образом, для разработчика представляет интерес выбор минимально необходимого порядка фильтра удовлетворяющего заданным требованиям.
Другими словами, предположим, что в изображенной на рис. 2 общей характеристике заданы максимально допустимое затухание в полосе пропускания 1 (дБ), минимально допустимое затухание в полосе задерживания 2 (дБ), частота среза с (рад/с) или fс (Гц) и максимальная допустимая ширина переходной области TW, которая определяется следующим образом
|
|
TW=1–2. |
(5) |
(Следовательно, полоса задерживания должна начинаться с некоторой частоты 21.) Задача состоит в нахождении минимального порядка n, который будет удовлетворять всем этим условиям.
Для фильтра Баттерворта минимальный порядок можно определить, подставив приведенные выше условия в (1) и решив его относительно порядка n. В результате получаем
|
|
|
(6) |
Уравнение (5) можно записать в виде
|
|
1/с=(TW/c)+1, |
(7) |
и полученное соотношение подставить в (6) для нахождения зависимости порядка n от ширины переходной области, а не от частоты 1. Параметр TW/c называется нормированной шириной переходной области и является безразмерной величиной. Следовательно, ТW и c можно задавать и в радианах на секунду, и в герцах.
Амплитудно-частотная характеристика фильтра Баттерворта наиболее плоская около частоты =0 по сравнению с характеристикой любого полиномиального фильтра n-го порядка и вследствие этого называется максимально плоской. Следовательно, для диапазона низких частот характеристика фильтра Баттерворта наилучшим образом аппроксимирует идеальную характеристику. Однако для частот, расположенных около точки среза и в полосе задерживания, характеристика фильтра Баттерворта заметно уступает характеристике Чебышева, который рассматривается ниже.
Однако фазочастотная характеристика фильтра Баттерворта лучше (более близка к линейной), чем соответствующие фазочастотные характеристики фильтров Чебышева, инверсных Чебышева и эллиптических сравнимого порядка. Это согласуется с общим правилом для фильтров данного типа – чем лучше амплитудно-частотная характеристика, тем хуже фазочастотная, и наоборот.
1.2. Фильтры Чебышева
Фильтр Чебышева обладает амплитудно-частотной характеристикой, которая определяется следующим образом:
|
|
|
(8) |
Параметры и К – постоянные числа, а Сn является полиномом Чебышева первого рода степени n и имеет вид:
|
|
Cn(x)=cos(narcos(x)). |
(9) |
Амплитудно-частотная характеристика достигает своего наибольшего значения К в тех точках, где Сn равно нулю. Поскольку эти точки распределены по полосе пропускания, то характеристика фильтра Чебышева содержит пульсации в полосе пропускания и монотонна в других областях. Размах этих пульсаций определяет параметр , а их число степень n. Коэффициент усиления фильтра определяется значением К.
Фильтр Чебышева иногда называют равноволновым фильтром, поскольку все пульсации равны по значению. Для К=1, т.е. на рис. 3 A=1, размах пульсаций RW=AA1 для фильтра Чебышева будет равен
|
|
|
(10) |
Таким образом, как угодно можно уменьшить RW, выбрав значение параметра достаточно малым.
Минимально допустимое затухание в полосе пропускания – постоянный размах пульсаций, часто выражается в децибелах как
|
|
|
(11) |
и может использоваться как характеристика фильтра Чебышева. Например, фильтр с неравномерностью передачи 1/2 дБ обладает таким значением , что =1/2 (это дает =0,3493). В общем случае, решая уравнение (11) относительно , можно получить
|
|
|
(12) |
Наибольшим допустимым размахом пульсаций обладает фильтр Чебышева с неравномерностью передачи 3 дБ, для которого в (11) =1 (если говорить более точно, то необходимо иметь значение =0,99763, поскольку 1оg10(2) не равен точно 0,3).
По
амплитудно-частотной характеристике
на рис. 1 определяем А=1,
а
![]() .
Для данного случая также можно точно
определить А2,
которое установило бы значение частоты
1.
Частота c=1
рад/с представляет собой точку среза
или граничную точку полосы частот с
пульсациями. Если интересуются значением
частоты 3дБ
,т. е. точкой, в которой характеристика
спадает на 3 дБ, то получают:
.
Для данного случая также можно точно
определить А2,
которое установило бы значение частоты
1.
Частота c=1
рад/с представляет собой точку среза
или граничную точку полосы частот с
пульсациями. Если интересуются значением
частоты 3дБ
,т. е. точкой, в которой характеристика
спадает на 3 дБ, то получают:
|
|
|
(13) |
Следует отметить, что c=3дБ если =1, и в этом случае получаем фильтр Чебышева с неравномерностью передачи 3 дБ.
На основе (8) для К=1 найдем минимальный порядок фильтра Чебышева:
|
|
|
(14) |
Амплитудно-частотная характеристика фильтра Чебышева данного порядка лучше амплитудно-частотной характеристики Баттерворта, так как у фильтра Чебышева уже ширина переходной области. Однако фазочастотная характеристика фильтра Чебышева хуже (более нелинейна) по сравнению с фазочастотной характеристикой фильтра Баттерворта. Фазочастотные характеристики фильтра Чебышева для 2–7-го порядков приведены на рис. 5. Для сравнения на рис. 5 штриховой линией изображена фазочастотная характеристика фильтра Баттерворта шестого порядка. Можно также отметить, что фазочастотные характеристики фильтров Чебышева высокого порядка хуже фазочастотных характеристик фильтров более низкого порядка. Это согласуется с тем фактом, что амплитудно-частотная характеристика фильтра Чебышева высокого порядка лучше амплитудно-частотной характеристики фильтра более низкого порядка.
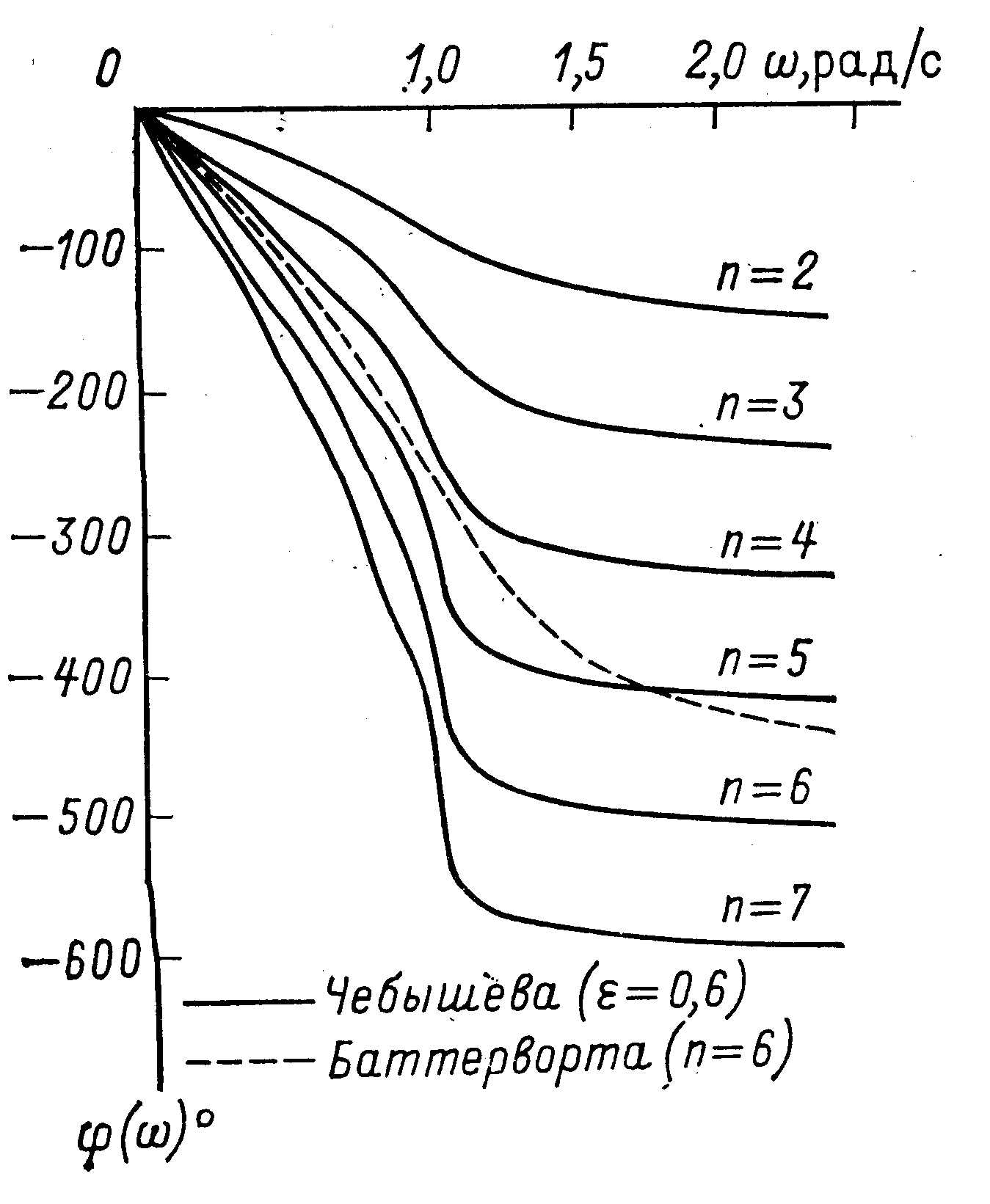
Рис. 5. Фазочастотные характеристики фильтров Баттерворта и Чебышева.
1.3. Эллиптические фильтры
Эллиптический фильтр имеет амплитудно-частотную характеристику, которая содержит пульсации как в полосе пропускания, так и в полосе задерживания и является лучшим среди всех фильтров нижних частот в том смысле, что для заданного порядка и допустимых отклонений характеристик в полосах пропускания и задерживания обладает самой узкой шириной переходной области. Пример амплитудно-частотной характеристики эллиптического фильтра пятого порядка изображен на рис. 6.
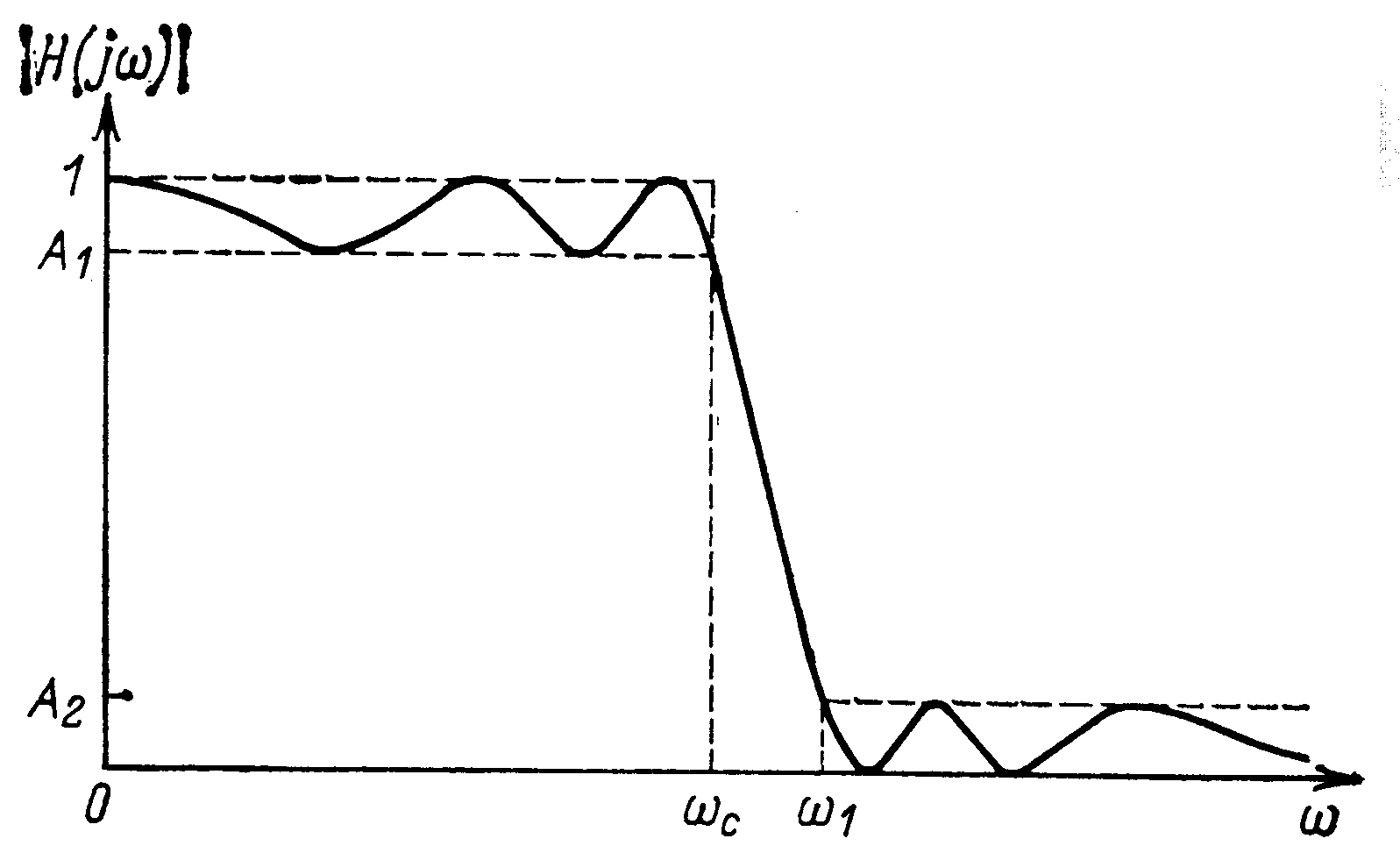
Рис. 6. Амплитудно-частотная характеристика эллиптического фильтра нижних частот для случая n=5.
Пульсации в полосе пропускания равны по значению и могут характеризоваться максимальным допустимым затуханием в полосе задерживания. Эта величина которую мы также будем называть неравномерностью передачи, в полосе пропускания (РRW), дБ, согласно обозначению на рис. 6 равна:
|
|
PRW=–20log10(A1). |
(15) |
Пульсации в полосе пропускания так же равны по значению (хотя не обязательно равны размаху пульсаций в полосе пропускания) и характеризуются минимальным затуханием в полосе задерживания МSL, дБ, следующим образом:
|
|
MSL=–20log10 (A2). |
(16) |
Ширина переходной области ТW, как и для других типов фильтров, составляет:
|
|
TW=1–c. |
(17) |
Для заданных значений РRW и МSL повышение порядка приводит к увеличению числа пульсаций в полосах пропускания и задерживания и уменьшению TW. Следовательно, можно задать обозначенные на рис. 6 параметры А1, A2 и c и, увеличивая порядок, достичь любого требуемого значения 1>c.
В виде произведения сомножителей передаточная функция эллиптическая фильтра нижних частот четного порядка n записывается следующим образом:
|
|
|
(18) |
а нечетного порядка n
|
|
|
(19) |
где А0, с0, Аi, аi, bi, ci – заданные постоянные числа.
Постоянные параметры аi, bi и ci вычисляются крайне сложно. Этот процесс требует знания эллиптических функций Якоби.

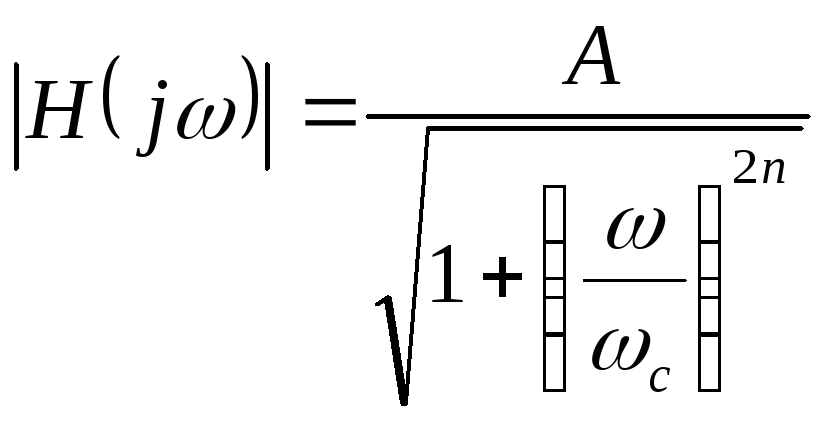 ,
(n=1,2,3…).
,
(n=1,2,3…).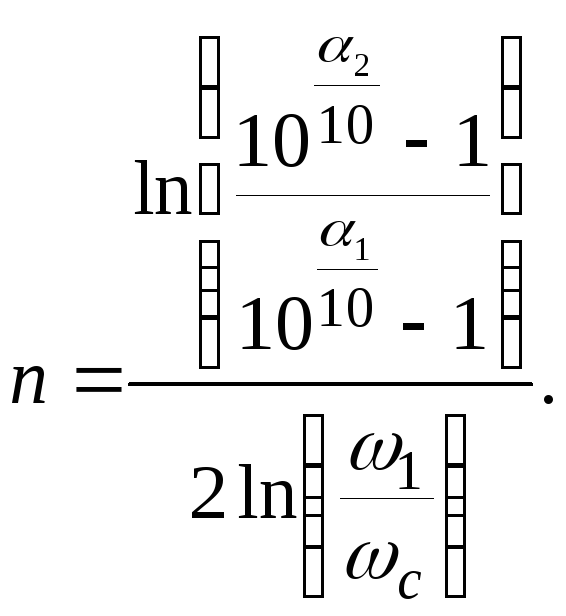
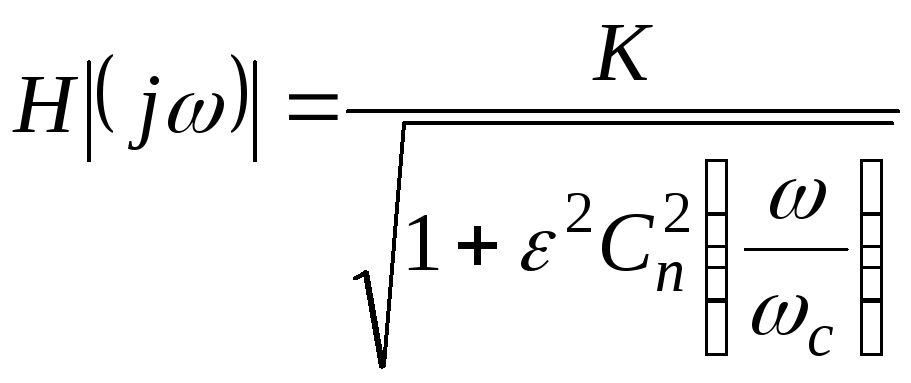 ,
(n=1,
2, 3...).
,
(n=1,
2, 3...).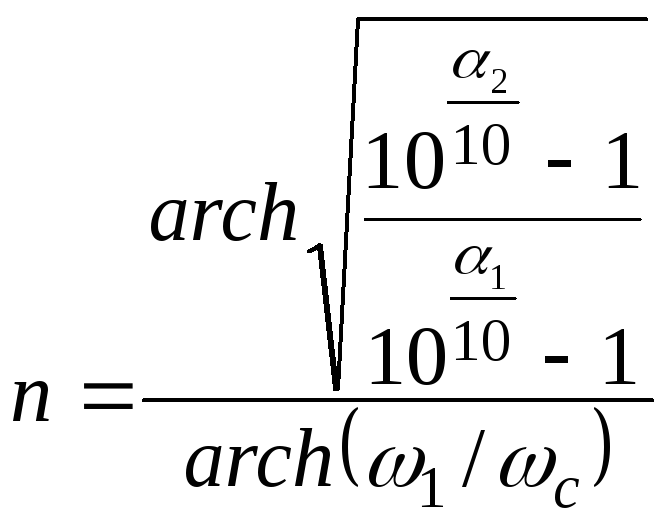 .
.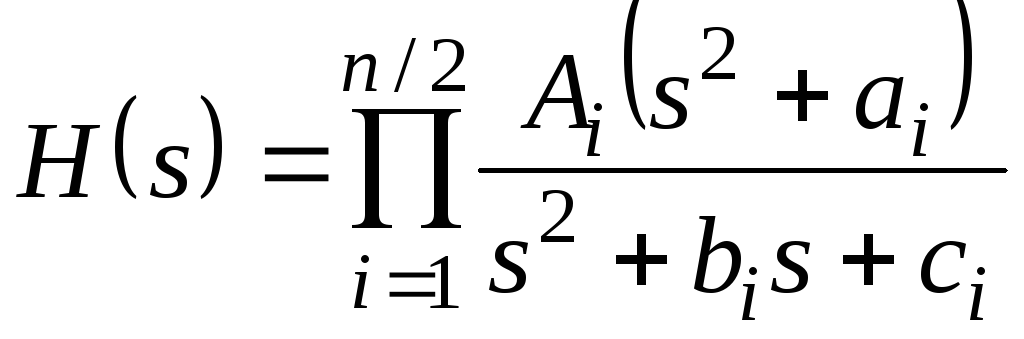 ,
,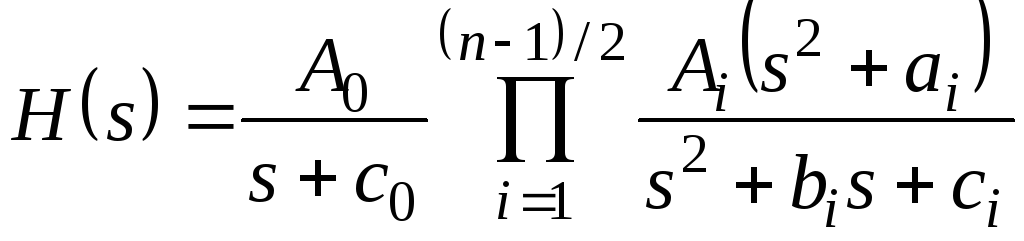 ,
,