Лабораторная работа № 8 Исследование теплоемкости металлов и сплавов
Цель работы. Изучить температурную зависимость теплоемкости металлов в области низких температур. Сравнить результаты измерений с классической и выводами квантовой теории металлов. Вычислить характеристическую температуру Дебая для исследованного металла.
8.1. Исходные теоретические сведения.
По представлениям квантовой физики внутренняя энергия кристаллической решетки складывается из нулевой энергии, которая не зависит от температуры, и из энергии фононного газа, непосредственно связанной с энергией температурных колебаний кристаллической решетки. Фононный газ состоит из квазичастиц – фононов, которые подчиняются квантовой статистике Бозе–Эйнштейна и возникают в процессе тепловых колебаний узлов решетки. Частотный спектр таких колебаний дискретен и имеет верхнюю границу максимально возможной частоты стоячих упругих волн, связанной с пространственными параметрами решетки и действующими в ней упругими силами.
Тепловая часть внутренней энергии колебаний кристаллической решетки массой в один моль u(T), согласно волновой теории П. Дебая и фононной теории квантовой механики, определяется выражением
,
(8.1.1)
где R – универсальная газовая постоянная; – характеристическая температура Дебая, своя у каждой кристаллической решетки; x – безразмерный параметр интегрирования.
Выражение для температуры Дебая имеет вид
,
(8.1.2)
где
– постоянная Планка; k
– постоянная Больцмана;
– скорость распространения упругих
волн в кристаллической решетке; n
– концентрация узлов решетки (число
узлов в единице объема).
Температура Дебая у многих металлов определена экспериментально. В качестве примера ее значения для наиболее распространенных металлов приведены в таблице 8.1.1.
Таблица 8.1.1.
|
Ag |
Au |
C |
Pb |
Mg |
Al |
Si |
Ti |
Cr |
Fe |
Ni |
Cu |
Zn |
|
225 |
165 |
2230 |
105 |
400 |
428 |
645 |
420 |
630 |
470 |
450 |
343 |
327 |
Безразмерный параметр интегрирования x пропорционален отношению температуры Дебая к температуре Т кристалла
.
(8.1.3)
Аналитическое выражение для молярной изохорной теплоемкости сv(T) в теории Дебая и квантовой механике имеет соответственно вид
.
(8.1.4)
При очень низких температурах, удовлетворяющих условию
,
(8.1.5)
интегральные функции (8.1.1) и (8.1.4) существенно упрощаются
,
(8.1.6)
.
(8.1.7)
Выражение (8.1.7) известно в физике как закон кубов Дебая, так как впервые теоретически объяснило результаты экспериментального исследования теплоемкости металлов, выполненные В. Нернстом вблизи абсолютного нуля температур.
В области высоких температур, удовлетворяющих условию
,
(8.1.8)
выражения (8.1.1), (8.1.4) для внутренней энергии и теплоемкости кристаллической решетки асимптотически приближаются к соответствующим выражениям классической молекулярной физики (в том числе к известному закону Дюлонга и Пти)
,
Дж/(мольК).
(8.1.9)
В переходной области умеренно низких температур, удовлетворяющих условию
,
(8.1.10)
Интегральная функция (7.1.4) для теплоемкости, ввиду ее сложности, табулирована. Некоторые ее значения представлены в таблице 8.1.2.
Таблица 8.1.2.
|
T/ |
0,05 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
2,0 |
|
|
cv |
0,24 |
1,88 |
9,16 |
14,5 |
17,9 |
20,5 |
21,6 |
22,5 |
23,0 |
23,3 |
23,6 |
24,5 |
24,9 |
|
cv/3R |
0,01 |
0,08 |
0,37 |
0,58 |
0,75 |
0,82 |
0,87 |
0,90 |
0,92 |
0,94 |
0,95 |
0,98 |
1,0 |
Расчет температуры Дебая проще всего производить, пользуясь законом кубов (8.1.7). Но из таблицы 8.1.1 следует, что в области температур (90 ... 300) К закон кубов у большинства металлов не выполняется. Поэтому в работе предлагается другой прием расчета температуры Дебая, непосредственно опирающийся на графическое представление функции (8.1.4).
У химически чистых металлов хорошо известны относительные атомные массы . Они указаны в любой таблице химических элементов (например, в периодической таблице Менделеева). У сплавов можно вычислить среднее значение , если известен химический состав сплава. Поэтому для грубых оценок температуры Дебая достаточно найти эффективную атомную массу исследованного образца (металлы имеют атомарную кристаллическую решетку, поэтому их атомная масса совпадает с мольной массой). Затем следует выбрать на низкотемпературной части экспериментальной кривой с(Т) произвольное значение удельной теплоемкости с(Тi) и вычислить молярную теплоемкость исследованного образца при температуре Тi.
.
(8.1.11)
Дальнейшие расчеты целесообразно провести, воспользовавшись универсальным графиком сv(T/), построенным на основе таблицы 8.1.2. Интересующий нас график показан на рис. 8.1.1. Чтобы определить по графику температуру Дебая, достаточно найти на кривой сv(T/) графика положение точки с молярной теплоемкостью с(Тi), затем спроектировать ее на ось абсцисс и получить искомое значение температуры Дебая .
Представление о степени достоверности проведенных исследований теплоемкости можно получить, вычислив температуру Дебая по нескольким значениям удельной теплоемкости с(Тi), взятым на разных участках экспериментальной кривой с(Т).
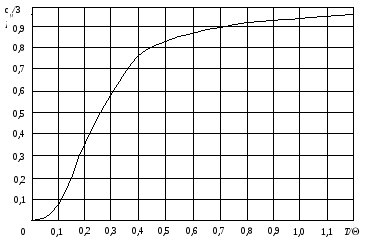
Рис. 8.1.1. График универсальной кривой (c/3R) = f(T/) по Дебаю.