4. Помехоустойчивость циклических кодов

Циклические коды можно использовать:

- для исправления ошибок;

- для обнаружения ошибок;

- для исправления и обнаружения ошибок.

5. Верность передаваемой информации

Наиболее предпочтительным является использование циклических кодов в режиме обнаружения ошибок, так как при этом достигается наибольшая верность передаваемой информации, определяемая по формуле

(1.5)

Использование циклических кодов для исправления ошибок приводит к снижению верности передаваемой информации, которая определяется по формуле (1.5), если исключить коэффициент и вместо параметра подставить параметр t, который определяет кратность гарантийно исправляемых циклическим кодом ошибок и связи с соотношением .

Режим одновременного исправления и обнаружения ошибок по достигаемой верности занимает промежуточное положение между рассмотренными режимами. Наиболее рациональными следует считать такие системы передачи дискретной информации, в которых циклические коды используются для обнаружения ошибок.

6. Потери информации

Потери информации имеют место в том случае, когда возникает ошибка, обнаруживаемая циклическим кодом, поэтому для обнаружения ошибок можно записать, что

(1.6)

где вероятность появления любой ошибки в кодовой комбинации.

7. Характеристика кодов с постоянной четностью единиц

Циклический (n, k)-код, построенный при помощи образующего полинома P(x) и не обладающий свойством постоянной четности единиц, может приобрести это свойство, если образующий полином P(x) домножить на двучлен (x+1) и формировать кодовые комбинации нового (n+1, k) – кода на основании полинома

(1.7)

В этом случае циклический (n+1, k) – код приобретает свойство дополнительно обнаруживать все ошибки нечетной кратности и, следовательно, для определения вероятности не обнаружения ошибок по выражению (1.5) необходимо увеличивать на единицу.

8. Алгоритмы расчета

9. Задаваемые для расчета технические параметры

Исходными данными для построения циклического кода являются:

- допустимое значение вероятности не обнаружения ошибок ;

- число информационных единичных элементов первичного кода k;

- вероятность искажения единичного элемента кодовой комбинации , характеризующая качество канала связи.

10. Описание алгоритма

На рисунке 1 приведена структурная схема алгоритма нахождения образующего полинома циклического кода, удовлетворяющего заданной верности.

1 На первом этапе, используя выражение (1.1), определяем n*, удовлетворяющее следующему условию:

(2.1)

2 По заданному k и найденному значению n*(m)определим число проверочных единичных элементов

(2.2)

3 Уточняем число проверочных единичных элементов по таблице в приложении 1, выбирая ближайшее табличное значение

4 Определяем табличное значение кратности гарантийно обнаруживаемых ошибок , соответствующее .

5 Так как табличные коды могут быть дополнены проверкой на четность, то определяем максимальную избыточность

и максимальную кратность гарантийно обнаруживаемых ошибок .

6 Уточняем длину кодовой комбинации циклического кода

.

Если n<n*(m), то будет иметь место так называемый укороченный циклический (n,k)-код, который по корректирующей способности эквивалентен полному циклическому -коду, число информационных единичных элементов которого больше на величину (n*-n).

7 Для найденных значений , используя выражение (1.5), определяем вероятность не обнаружения ошибок .

8 Проверяем логическое условие

9 При невыполнении условия (2.3) выбираем n*(m+1) и повторяем п. 2-8.

10 Если условие (2.3) выполняется, то методом перебора определяем минимальное число проверочных единичных элементов и соответствующие значения и , для которых выполняется условие (2.3).

11 Выбираем образующий полином P(x) по таблицам (приложение 1), соответствующий вычисленным значениям и

,

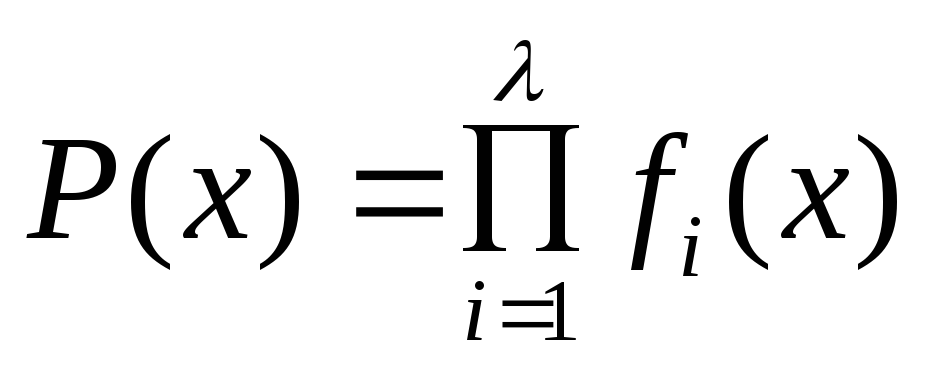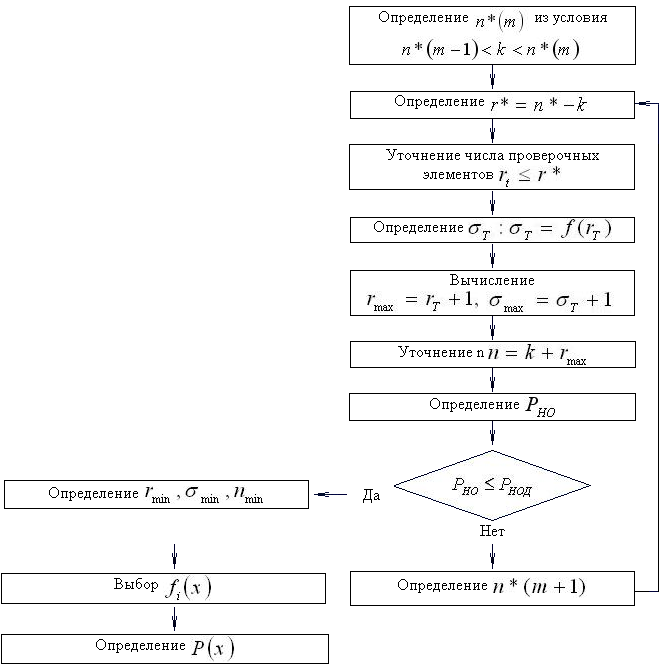
Рисунок 1. Структурная схема алгоритма нахождения образующего

полинома циклического кода

(2.3)

где - неприводимые многочлены, индекс которых возрастает с увеличением числа проверочных элементов ;

- индекс соответствующий .

При введении дополнительной проверки на четность

.

С целью сокращения записи все многочлены в приложении В указаны в восьмеричном представлении. При такой записи каждый символ обозначает три двоичных знака в соответствии со следующим кодом:

0<=>000	4<=>100
1<=>001	5<=>101
2<=>010	6<=>110
3<=>011	7<=>111.

Коэффициенты многочленов в двоичной записи расположены в порядке убывания, так что коэффициент при слагаемом высшего порядка расположен слева. Например, число 45 в коде n*=31 обозначает многочлен 5-ой степени. В двоичной записи этому числу эквивалентно число

100 101

и соответствующий многочлен равен

.