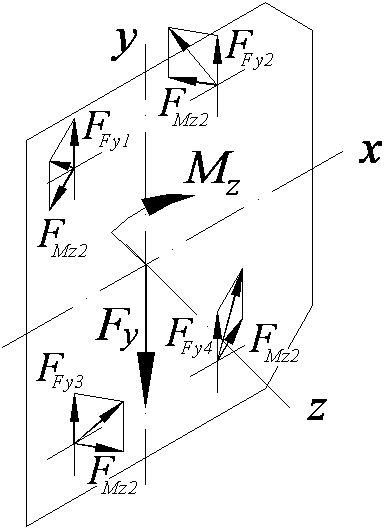2.1.10 Расчет групповых резьбовых соединений

Расчет групповых резьбовых соединений сводится к определению наиболее нагруженного болта (винта, шпильки) и к оценке его прочности по формулам рассмотренных выше случаев нагружения одиночного болта (см. п. 2.1.9).

Так как распределение нагрузки между болтами достаточно сложное и зависит от многих факторов, то для упрощения расчетов принимается ряд допущений:

• Поверхности стыка соединяемых деталей должны иметь как минимум две оси симметрии для облегчения определения зависимости распределения нагрузки между болтами;

• Все болты соединения должны быть одинаковыми, одинаково затянуты и расположены симметрично относительно осей симметрии стыка;

• При нагружении соединения деформируются только болты и часть материала соединяемых деталей вблизи болтов. Сами детали предполагаются абсолютно жесткими.

Приложенная к соединению нагрузка может вызвать раскрытие стыка соединяемых деталей (продольная нагрузка, п. 2.1.9.3) и (или) сдвиг деталей (поперечная нагрузка, п. 2.1.9.4).

2.1.10.1 Расчет соединения, несущего продольную нагрузку, проходящую через центр соединения (рис. 2.19)

а	б
Рис. 2.19. Расчет соединения, несущего продольную нагрузку

Так как соединение симметричное, а кронштейн считается абсолютно жестким, то нагрузка, приложенная к кронштейну, равномерно распределяется между болтами:

,

где , , …, – нагрузка, приходящаяся на один болт;

F – продольная нагрузка, приложенная к кронштейну;

n – количество болтов в соединении.

После определения , ведется расчет одиночного болта как затянутое нагруженное соединение (см. п. 2.1.9.3):

.

При проектировочном расчете внутренний диаметр резьбы:

.

2.1.10.2 Расчет соединения, несущего поперечную нагрузку

Расчет соединения, несущего поперечную нагрузку в плоскости соединения рассмотрим на примере кронштейна (рис. 2.20). Приложенная к нему сила F стремится повернуть кронштейн относительно центра соединения (точки O) и сдвинуть его в плоскости стыка. Таким образом, болты работают на удержание деталей от сдвига в поперечном направлении.

Для облегчения расчета силу F (рис. 2.20а) переносим в центр соединения и, по правилам теоретической механики, добавляем момент M (рис. 2.20б), равный:

.

а	б
Рис. 2.20. Расчет соединения, несущего поперечную нагрузку

Рассмотрим распределение нагрузки между болтами соединения отдельно от воздействия силы F и от воздействия момента M.

От действия силы F нагрузка распределяется равномерно между всеми болтами соединения (рис. 2.21а):

,

где n – число болтов в соединении.

а	б	в
Рис. 2.21. Определение нагрузки, приходящейся на один болт

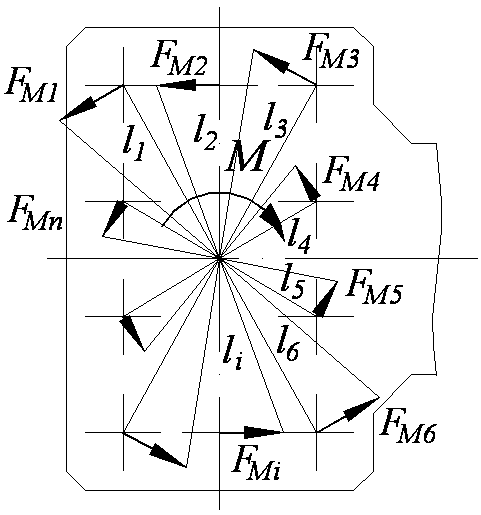
Нагрузка от действия момента M зависит от расстояния от центра соединения до конкретного болта (рис. 2.21б):

.

Поэтому неизвестные силы можно выразить через одну:

; ; …; ;

Момент M равен суммарному моменту сил относительно центра соединения:

.

.

Отсюда:

.

Зная нагрузки , и закономерность распределения их в соединении (рис. 2.21в), определяется суммарная нагрузка, действующая на болт:

или .

Наибольшая из сил будет расчетной. Далее, самый нагруженный болт рассчитывается как одиночное резьбовое соединение, несущее поперечную нагрузку (см. п. 2.1.9.4):

,

где – коэффициент трения; для стальных стыков = 0,1…0,2.

При проектировочном расчете внутренний диаметр резьбы:

.

2.1.10.3 Расчет соединения, несущего комбинированную нагрузку

Болты, крепящие кронштейн (рис. 2.22а), удерживают его как от раскрытия стыка (отрыва от стены), так и от сдвига относительно стены (сдвига деталей). Для упрощения расчетов приложенная к кронштейну сила разбивается на составляющие и , переносится в центр соединения, и добавляются соответствующие моменты , , (рис. 2.22а):

; ; .

а	б
Рис. 2.22. Схема к расчету соединения, несущего комбинированную нагрузку

Далее рассматривается воздействие на болты соединения этих нагрузок по отдельности.

Сила , моменты и стремятся к отрыву кронштейна от стены.

Сила равномерно распределяется между болтами (рис. 2.23а):

,

где n – количество болтов в соединении.

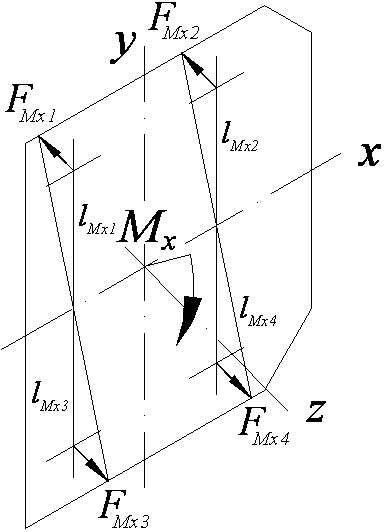
Величина растягивающих болты сил и , вызываемых моментами и прямо пропорциональна расстоянию от оси x и y соответственно (рис. 2.23б,в):

; .

а	б	в	г
Рис. 2.23. Схема к расчету отрывающих сил

Моменты и равны соответственно суммарным моментам сил и относительно осей x и y:

;

.

Отсюда:

; .

Суммарная отрывающая сила определяется с учетом направления действия составляющих ее сил (рис. 2.23г):

.

Сила F_y и момент M_z стремятся к сдвигу деталей в плоскости соединения.

а	б	в
Рис. 2.24. Схема к расчету сдвигающих сил

Сила равномерно распределяется между болтами (рис. 2.24а):

,

где n – количество болтов в соединении.

Величина сдвигающей болт силы , вызываемой моментом прямо пропорциональна расстоянию ее от оси z (рис. 2.24б):

.

Момент равен суммарному моменту сил относительно осей z:

.

Отсюда:

.

Суммарная сдвигающая сила определяется с учетом направления действия составляющих ее сил (рис. 2.24в):

или .

Прочность болта должна быть достаточна для того, чтобы выдержать растягивающую силу и силу затяжки, необходимую для обеспечения неподвижности деталей под действием сдвигающей силы . Отсюда растягивающие напряжения с учетом кручения:

.

При проектировочном расчете внутренний диаметр резьбы:

.