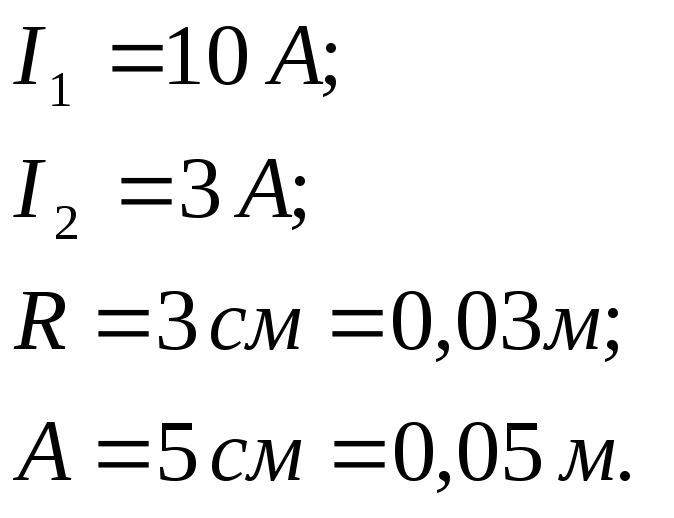Примеры решения задач

Пример 1. Сфера радиусом R=5 см и бесконечная плоскость равномерно заряженные с поверхностной плотностью заряда ₁=10нКл/м² и ₁=–15нКл/м² соответственно. Центр сферы находится на расстоянии ℓ=10см от плоскости. Найти напряженность электростатического поля в точке А, что находится на расстоянии а=5см от поверхности сферы и b=10см от плоскости; силу, которая будет действовать на точечный заряд q₀=0,1нКл, если его поместить в точку А.

Дано: 1=10нКл/м2=1010–9Кл/м2 2=–15нКл/м2=–1510–9Кл/м2 R=5 см =510–2 м ℓ=10 см =1010–2 м а=5см=510–2 м b=10см =1010–2 м q0=0,1нКл=0,110–9Кл
Найти: Е, F – ?	Решение.

В соответствии с принципом суперпозиции электрических полей, каждый заряд создает поле независимо от нахождения в пространстве других зарядов. Поэтому общая напряженность равна векторной сумме отдельных напряженностей:

Напряженность поля сферы в воздухе на расстоянии r от его центра

(1)

где ₀ – электрическая постоянная; Q₁ – заряд сферы.

Выразим заряд сферы через поверхностную плотность заряда s₁ и площадь поверхности сферы (S=4R²), а расстояние r от точки А к центру сферы через расстояние a к поверхности сферы и радиус сферы R

Подставив эти выражения в формулу (1), получим

. (2)

Напряженность поля плоскости равномерно заряженной с поверхностной плотностью s₂

(3)

Вектор направлен по силовой линии от сферы, так как сфера заряжена положительным зарядом, вектор направлен к плоскости, так как она заряженная отрицательно.

Модуль вектора найдем по теореме косинусов

,

но так как векторы и взаимно перпендикулярны и cos90^О=0, то

. (4)

Подставив (2) и (3) в (4) и вынося общий множитель 1/₀ за знак корня, получим

. (5)

2. Величину силы, которая действует на точечный заряд , который находится в электростатическом поле, находим по формуле

(6)

Проверяем дает ли формула (5) единицу напряженности В/м, а формула (6) единицу силы Н.

Подставим в формулу (5) и (6) значение величин в единицах СИ и сделаем вычисления

Направление силы совпадает с направлением вектора . (так как ), что и показано на рисунке.

Ответ: ,

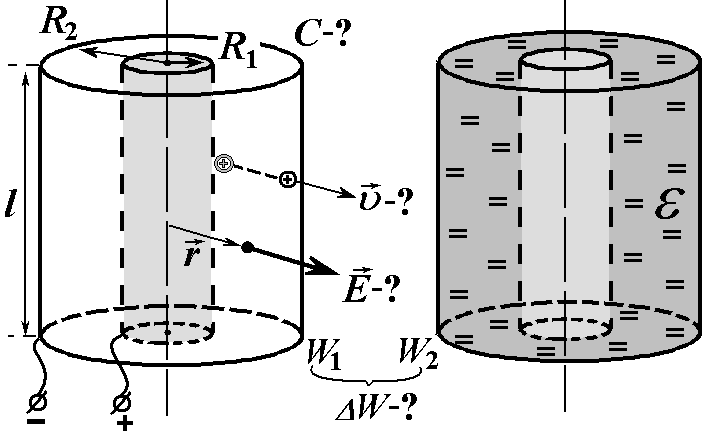
Пример 2. Воздушный цилиндрический конденсатор состоит из двух коаксиальных цилиндров радиусами R₁ =1см и R₂ =3см. Длина обкладок конденсатора L=50см. Конденсатор зарядили с разностью потенциалов U=100B и отключили от источника.

Найти: 1) электроемкость конденсатора; 2) напряженность поля в конденсаторе на расстоянии r=2см от оси цилиндра; 3) скорость, которую будет иметь протон перемещаясь под действием сил поля от одной обкладки конденсатора к второй; 4) на сколько изменится энергия конденсатора, если пространство между цилиндрами заполнить парафином ( ).

Дано:; R1= 1cм =0,01м; R2=3см = 0,03м; L=50 cм =0.5м; r =2см =0,02м;
Найти: С; E; ; W – ?	Решение:

Электроемкость воздушного =1 цилиндрического конденсатора находится по формуле

(1)

где ₀ – электрическая постоянная; L – длина обкладок конденсатора; R₁ и R₂ – радиусы цилиндров.

Для нахождения напряженности поля на расстоянии r от оси цилиндров, например, в точке А, используем принцип суперпозиции электрических полей

,

где – напряженность поля в точке А, созданная внутренним цилиндром; – напряженность поля внешнего цилиндра в той же точке. Так как напряженность необходимо найти на расстоянии r<R₂ , то Е₂=0 и Е=Е₁. Допуская, что цилиндр довольно длинный (), необходимую напряженность находим по формуле расчета напряженности поля бесконечно длинного цилиндра

(2)

где - линейная плотность заряда цилиндра. Заряд конденсатора Q, связанный с напряжением U между его обкладками соотношением

Q=CU. (3)

Подставив в формулу (2) выражения для  и Q, получим

(4)

Протон из состояния покоя, перемещаясь под действием сил поля конденсатора, изменяет свою конечную энергию на величину, равную работе сил поля

Т₂ – Т₁=А,

где Т₂ , Т₁ – значения кинетической энергии протона в начальной и конечной точках пути. Если у протона не было начальной скорости, то Т₁=0 и

, (5)

где m – масса протона;  – его конечная скорость.

Работа сил поля находится как произведение заряда протона, равного элементарному заряду q_P= e на разность потенциалов U

A=eU. (6)

Приравняв правые части уравнений (5) и (6), получим

,

откуда (7)

При заполнении конденсатора парафином его энергия изменится на величину

(8)

где W – энергия воздушного конденсатора; W’ – энергия конденсатора с парафином.

Энергия конденсатора с зарядом Q и емкостью С находится по формуле

(9)

Так как конденсатор отключен от источника, то заряд Q на его обкладках при заполнении парафином останется без перемен. Электроемкость конденсатора после заполнения парафином изменится, и будет равняться

тогда (10)

Подставив (9) и (10) в (8) и вынося общий множитель за скобки, получим

или с учетом формулы (3) изменение энергии конденсатора

Подставим числовые значения в расчетные формулы (1), (4), (7) и (11) и выполним вычисления:

Таким образом, энергия отключенного конденсатора при внесении диэлектрика уменьшается (). Это связано с тем, что силы поля конденсатора поляризуют диэлектрик и втягивают его в область большей напряженности.

Ответ: , , .

Пример 3 Электрическая цепь состоит из двух источников ЭДС e₁=20В, e₂=5В и трех сопротивлений R_1, R₂=19Ом и R₃=10Ом. Внутренние сопротивления источников r₁=2Ом, r₂=1Ом, а через сопротивление R₁ проходит ток I₁=0,2 А в направлении, указанном на рисунке.

Найти: 1) сопротивление R₁ и силы токов, которые проходят через сопротивления R₂ и R₃; 2) разность потенциалов между точками А и В.

Дано: 1=20 В 2=5 В r1=2 Ом r2=1 Ом R2=19 Ом R3=10 Ом I1=0,2 А
Найти: I2, I3, R1, В–А–?	Решение:

1. Для расчета разветвленных цепей используют правила Кирхгофа.

Чтобы найти сопротивление и два значения силы тока, необходимо составить три уравнения. Перед складыванием уравнений необходимо произвольно выбрать: а) направление токов (если они не заданы в условии); б) направление обхода контуров. Направление тока I₁ задано, направление токов I₂ и I₃ выберем так, как на схеме, и договоримся обходить контуры по часовой стрелке (пунктирная линия на схеме). Данная схема имеет два узла: А и В. При составлении уравнений по первому правилу Кирхгофа необходимо учесть, что ток, который подходит к узлу, входит в уравнения со знаком плюс, а ток, который выходит от узла – со знаком минус.

По первому закону Кирхгофа для узла А

(1)

Для узла В составлять уравнение не имеет смысла, так как оно сводится к уравнению (1).

Необходимые еще два уравнения получим по второму правилу Кирхгофа. При этом необходимо придерживаться следующих правил знаков: а) падение напряжения (произведение IR или Ir) входит в уравнение со знаком плюс, если направление тока совпадает с направлением обхода контура, в другом случае – со знаком минус; б) ЭДС входит у уравнения со знаком плюс, если она увеличивает потенциал в направления обхода контура (переход происходит от минуса к плюсу в середине источника), в другом случае – со знаком минус.

По второму правилу Кирхгофа для контуров

; (2)

. (3)

Подставив в уравнения (1), (2), (3) значение заданных величин, получим систему уравнений

или

Выразим I₃ из уравнения (4) и подставим в уравнения (6)

.

Откуда

Знак минус в значении тока I₂ означает, что направление тока I₂ было выбрано противоположным действующему. В реальности ток I₂ протекает от узла В к узлу А.

Из уравнения (4) находим I₃:

Из уравнения (5) находим R₁

Ом.

2. Разность потенциалов U=Dj_A,B=j_B–j_A можно найти, если записать закон Ома для неоднородного участка цепи, например

(7)

В законе Ома уже учтено, что положительное направление силы тока совпадает с направлением работы сторонних сил источника, которое соответствует увеличению потенциала. Тогда искомая разность потенциалов

Выполняем вычисления

.

Ответ: I₂=–0,1 A; I₃=0,3 А; R₁=83 Ом, .

Пример 4 Бесконечно длинный прямолинейный проводник расположен перпендикулярно плоскости кругового контура и находится на расстоянии a=5см от его центра. Сила тока в проводнике , сила тока в контуре , направление тока показано на рисунке. Радиус контура R=3см. Найти индукцию магнитного поля в центре контура.

Дано:
Найти: В – ?

Решение: В соответствии с принципом суперпозиции магнитных полей индукция магнитного поля в центре кругового контура равняется векторной сумме магнитных индукции и полей, которые создаются в этой точке токами и :

Проводник с током расположенный в плоскости рисунка, ток по проводнику идет к наблюдателю. Для нахождения направления вектора проводим силовую линию (пунктирная линия на рис.4), находим ее направления по правилу буравчика и по касательной к ней в заданной точке строим Вектор по правилу буравчика направленный перпендикулярно плоскости рисунка от наблюдателя. На рис.4 показанные направления векторов вектор и в двух проекциях. Так как векторы и взаимно перпендикулярные, модуль вектора

Находим по теореме Пифагора

. (1)

Индукция магнитного поля бесконечно длинного прямолинейного проводника с током в вакууме (или воздухе) находим по формуле

, (2)

где – магнитная постоянная; – расстояние от проводника к точке, где надо найти магнитную индукцию.

Индукция магнитного поля в центре кругового контура радиусом R

Подставляя (2) и (3) в формулу (1) и учитывая, что в данном случае =a, получим:

или (4)

Проверяем дает ли правая часть формулы (4) единицу магнитной индукции (Тл)

Выполним вычисления:

Ответ:

Пример 5 По бесконечно длинному проводнику, согнутом так, как показано на рисунке, протекает ток I=5А. Радиус дуги R=5см. Найти напряженность магнитного поля в точке О.

Дано: I=5 А. R=5 см
Найти: Н – ?

Решение. Напряженность магнитного поля в точке О найдем используя принцип суперпозиции полей. В данном случае провод можно разбить на 6 участков: 4 прямолинейных (1,3,5 и 6) и две дуги полукругов (2 и 4). Напряженность магнитного поля в точке О равная векторной сумме напряженностей полей, которые возникли из участков в этой точке

Напряженность магнитного поля, которое создается элементом длины проводника с током, находится по закону Био-Савара-Лапласа

,

где – радиус вектор, проведенный от до точки, где находится напряженность .

Так как точка О лежит на оси участков 1 и 3, то для любого элемента этих участков Поэтому

Направления векторов напряженности найдем по правилу буравчика. Вектор направлен перпендикулярно плоскости рисунка от наблюдателя, векторы – к наблюдателю. Учитывая направление к наблюдателю, заменим векторное равенство (1) скалярной.

Модуль вектора найдем, используя формулу расчета для напряженности поля в центре кругового тока

В данном случае магнитное поле создается лишь половиной такого кругового тока, поэтому

(3)

Аналогично для участка 2

(4)

Модули векторов и находим, используя формулу расчета для напряженности поля, которое создается отрезком проводника с током

где – наименьшее расстояние от проводника к точке, где находится напряженность; и – углы, которые создаются проводником и радиус-векторами, проведенными из концов проводника к этой точке. Для участка 5 r₀=R; ₁=90⁰; cos ₁=0; ₂=/4; cos ₂= .

Тогда

Аналогично для участка 6

₁=/4; cos ₁= ; ₂ 0 (провод бесконечно длинный), cos ₂1.

Подставив (3), (4),(5) и (6) в формулу (2), получим

или

. (5)

Проверяем дает ли правая часть формулы (5) единицу напряженности магнитного поля (А/м)

Выполним вычисления:

Ответ:

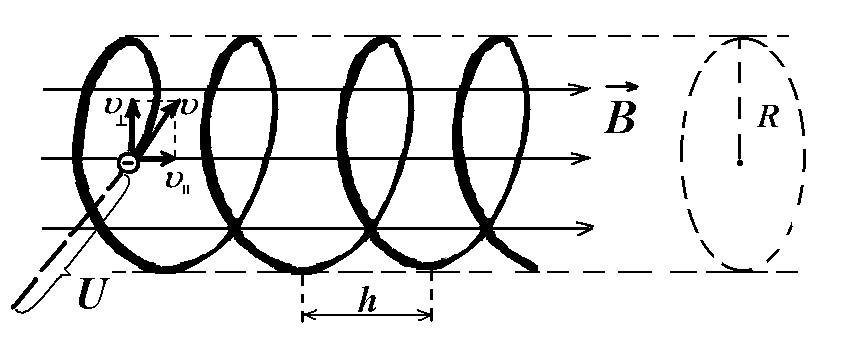
Пример 6 Электрон, ускоренный разностью потенциалов U, влетает в однородное магнитное поле с индукцией В = 5мТл и двигается по винтовой линии с шагом h = 4 см. и радиусом R=1см. Найти ускоренную разность потенциалов U, которую прошел электрон.

Дано: В = 5мТл = 5×10-3 Тл; h = 4см = 0,04м.; R = 1см = 0,01м. m = 9,11×10-31кг; e = -1,6×10-19Кл.
Найти: U – ?

Решение: Электрон, проходя ускоряющую разность потенциалов U, приобретет кинетическую энергию m²/2, равную работе сил ускоряющего поля

откуда

где m – масса электрона;  – скорость, приобретенная электроном в ускоряющем поле; е – заряд электрона. Таким образом, для нахождения ускоряющей разности потенциалов необходимо найти скорость, с которой электрон попадает в магнитное поле.

Так, как электрон в магнитном поле двигается по винтовой линии, то его скорость составляет некоторый угол (  /2) с линиями магнитной индукции (см. рисунок). Раскладываем вектор на две составляющие: – параллельную вектору магнитной индукции и перпендикулярную ему . На электрон, который двигается в магнитном поле, действует сила Лоренца

.

Модуль этой силы

Скорость в магнитном поле не изменяется (=0) и обеспечивает перемещение электрона вдоль силовой линии. Перпендикулярную составляющую скорости сила Лоренца изменяет только по направлению ( ), создавая нормальное ускорение

где R – радиус винтовой линии. Таким образом, электрон одновременно принимает участие в двух движениях: равномерном перемещении со скоростью и равномерном движении по окружности со скоростью (в отсутствии параллельной составляющей электрон двигался бы по окружности в плоскости, перпендикулярной силовым линиям).

По второму закону Ньютона

Приравнивая правые части (2) и (3) , найдем перпендикулярную составляющую скорости

;

Параллельную составляющую найдем из следующих соображений. За время, равное периоду оборота электрона Т, в направлении линий индукции электрон переместится со скоростью на расстояние, равное шагу винтовой линии h .

Тогда

где Т =2R/_ .

После подстановки из формулы (4) и сокращение на R , получим

Найдем выражение для Т подставим в формулу (5)

Квадрат модуля скорости, как видно из рисунка, можно выразить через и :

,

или с учетом (4) и (6)

Подставив в формулу (1) выражение (7) и выполнив необходимые сокращения, найдем искомую разность потенциалов

(R² + ).

Проверим, дает ли правая часть расчетной формулы единицу разности потенциалов (В):

.

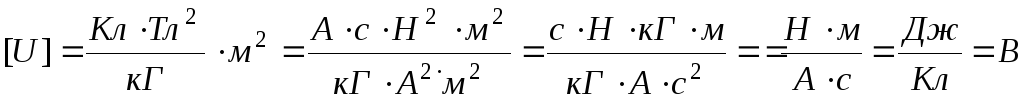Выполним вычисления:

Ответ:

Пример 7 В середине длинного прямого соленоида, который имеет n₀=10 витков на сантиметр, размещенный круговой контур площадью S = 10 см². Плоскость контура расположена под углом  = 30⁰ к оси соленоида (см. рисунок). По обмотке соленоида протекает ток I = 5A. Какая средняя ЭДС приводится в круговом контуре, если за время t = 10 мс направление тока в обмотке изменить на противоположный?

Дано: n0 = 10 см –1 = 103 м–1 S = 10 см 2 = 10 –3 м 2;  = 30 0; І =5А; t = 10 мс = 10 –2 с.
Найти: – ?

Решение: При изменении тока в обмотке соленоида изменится и магнитный поток Ф, что пронизывает круговой контур. Вследствие этого в контуре возникнет ЭДС индукции, которая находится по закону электромагнитной индукции  = -dФ/dt. По этой формуле находят мгновенное значение ЭДС индукции, среднее значение находят из средней скорости изменения магнитного потока с течением времени

= (1)

где - изменение магнитного потока за промежуток времени . Поле в средней части длинного соленоида будет однородной. В этом случае магнитный поток находится по формуле: , где В – индукция магнитного поля соленоида; S – площадь контура; – угол между вектором и нормалью к плоскости контура. Индукция магнитного поля в середине длинного соленоида

где – магнитная постоянная; – магнитная проницаемость среды (в воздухе =1) I – сила тока в обмотке соленоида; – количество витков на единицу длины.

Выберем направление тока в обмотке соленоида так, как это показано на рисунке ( ), и по правилу винта найдем соответствующим ему направление вектора . Магнитный поток в этом случае

После изменения направления тока на противоположный изменит свое направление и вектор магнитной индукции ( ).

Магнитный поток

(3)

(здесь учтено, что ). Подставляя в формулу (1) выражения и учитывая, что - (см. рисунок), получаем

Проверим дает ли правая часть расчетной формулы единицу разности ЭДС (В):

выполним вычисления

Ответ:

Пример 8 В однородном магнитном поле с индукцией В=0,5 Тл равномерно вращаеться короткая катушка, которая состоит из N=100 витков площадью S=100 см². Ось обращения лежит в плоскости витков катушки и перпендикулярная линиям индукции магнитного поля (см. рисунок). Найти: максимальную ЭДС, которая приводится в катушке при ее обращении с периодом Т=0,1 с; заряд, который проходит по катушке при изменении угла между осью катушки и вектором магнитной индукции от , если сопротивление катушки .

Дано: В=0,5 Тл, N=100, S=100 см, Т=0,1 с, φ1=0, φ2=90 о
Найти: max ; Q – ?

Решение: При обращении катушки изменяется магнитный поток, который пронизывает катушку, и в соответствия с законом электромагнитной индукции в катушке возникает ЭДС индукции

(1)

где магнитный поток в однородном магнитном поле с индукцией В находится по формуле:

(2)

где S – площадь витков;  – угол между нормалью к плоскости витков катушки и вектором ; N – количество витков, которые пронизываются потоком Ф. При равномерном обращении за время t катушка повернется на угол =t,  – угловая скорость вращения, связана с периодом соотношением

Подставив в формулу (2) выражения  и  получим

(3)

Для нахождения мгновенного значения ЭДС индукции найдем, подставив в формулу (1) выражение для магнитного потока и продифференцируем по времени

Значение ЭДС будет максимальной в тот момент времени, если

Тогда _. (4)

Для нахождения заряда Q, что проходит по катушке, применим закон Ома для замкнутой цепи

(5)

где R – сопротивление катушки; – мгновенное значение силы тока в катушке.

Приравнивая правые части уравнений (1) и (5), получим

Так как мгновенное значение силы тока то это уравнение можно переписать в виде

откуда (6)

Если взять интеграл из выражения (6), то найдем заряд, который проходит по катушке при изменении магнитного потока от Ф₁ до Ф₂:

. (7)

При изменении угла между осью катушки и вектором от j₁ к j₂, магнитный поток изменится отдо. Подставив выражения Ф₁ и Ф₂ в формулу (7), найдем искомый заряд:

. (8)

Проверим дает ли правая часть формулы (4) единицу ЭДС (В), а правая часть формулы (8) единицу заряда (Кл):

;

.

Выполним вычисления:

;

Ответ: , .

ЗАДАЧИ

Задача 1.1 Решить в соответствии со своим вариантом одну из приведенных ниже задач. Номер задачи и все необходимые данные приведены в табл. 1.1. Если в номере задачи есть буквенный индекс, то следует отвечать только на вопрос, который соответствует этому индексу.

1 Электростатическое поле создается двумя бесконечными параллельными плоскостями, которые заряжены равномерно с поверхностными плотностями σ₁ и σ₂. Найти силу, которая действует в этом поле на точечный заряд Q₁ , если заряд находится: а) между плоскостями; б) за пределами плоскостей.

2 Точечный заряд Q₁ находится в центре равномерно заряженной сферы радиусом R. Найти напряжённость электростатического поля в двух точках, которые лежат от центра на расстоянии r₁ и r₂, если: а) заряд сферы равняется Q₂ ; б) поверхностная плотность заряда сферы равна σ₂.

3 Длинная нить, равномерно заряженная с линейной плотностью τ₁, расположена на оси длинного цилиндра, радиус которого R. Цилиндр равномерно заряжен с линейной плотностью τ₂. Найти напряженность электростатического поля в двух точках: 1) на расстоянии r₁ от нити; 2) на расстоянии l от поверхности цилиндра.

4 Две длинных параллельных нити равномерно заряжены с линейными плотностями τ₁ и τ₂. Расстояние между нитями равняется l. Найти напряжённость электростатического поля в точке, которая находится на расстоянии r₁ от первой нити и r₂ от второй нити.

5 Электростатическое поле создается равномерно заряженными бесконечной плоскостью и сферой. Поверхностная плотность заряда плоскости σ₁. Радиус сферы R, поверхностная плотность заряда σ₂. Центр сферы находится на расстоянии l от плоскости. Найти напряжённость поля в точке, которая находится между сферой и плоскостью на расстоянии r₁ от плоскости.

Задача 1.2 Решить одну из следующих задач. Номер задачи и все необходимые данные приведены в табл. 1.2.

1 Сферический воздушный конденсатор состоит из двух концентрических сфер с радиусами R₁ и R₂. Конденсатор заряжен с некоторой разностью потенциалов. В табл. 1.2 заданы по вариантам R₁ , R₂ и одна из следующих величин:

Q – заряд на обкладках конденсатора;

U – разность потенциалов между обкладками;

υ – скорость, которую приобретёт электрон, проходя под действием сил поля от одной обкладки к другой.

Найти: 1) величину, указанную в последней колонке таблицы; 2) напряжённость поля в конденсаторе на расстоянии r от центра сферы; 3) энергию конденсатора.

2 Цилиндрический воздушный конденсатор состоит из двух коаксиальных цилиндров радиусами R₁ и R₂. Длина конденсатора L. Конденсатор заряжен с некоторой разностью потенциалов. В табл. 1.2 заданы по вариантам размеры конденсатора и одна из следующих величин:

Q – заряд на обкладках конденсатора;

U – разность потенциалов между обкладками;

υ – скорость, которую приобретёт протон, пройдя под действием сил поля от одной обкладки к другой.

Найти: 1) величину, указанную в последней колонке таблицы; 2) напряжённость поля в конденсаторе на расстоянии r от оси цилиндра; 3) энергию конденсатора.

3. Плоский воздушный конденсатор с площадью пластин S и расстоянием между пластинами d зарядили и отключили от источника. В табл. 1.2 заданы по вариантам размеры конденсатора и одна из следующих величин:

Q – заряд на обкладках конденсатора;

U – разность потенциалов между обкладками;

E – напряженность поля в конденсаторе;

υ – скорость, которую приобретёт электрон, перемещаясь под действием сил поля от одной обкладки к другой.

Найти: 1) величину, указанную в последней колонке таблицы; 2) насколько изменится энергия конденсатора, если расстояние между его пластинами увеличить в два раза.

4 Плоский воздушный конденсатор с площадью пластин S и расстоянием между пластинами d подключён к источнику электрической энергии. В табл. 1.2 заданы по вариантам размеры конденсатора и одна из следующих величин:

Q – заряд на обкладках конденсатора;

U – разность потенциалов между обкладками;

E – напряженность поля в конденсаторе;

υ – скорость, которую приобретёт протон, перемещаясь под действием сил поля от одной обкладки к другой.

Найти: 1) величину, указанную в последней колонке таблицы; 2) насколько изменится энергия конденсатора, если, не отключая конденсатор от источника, пространство между его пластинами заполнить диэлектриком с диэлектрической проницаемостью ε.

Примечание. Переписывая условие задачи, перечисляйте только те величины, которые относятся к данному варианту, и укажите их численные значения.

Задача 1.3 Составьте схему из трех соединенных участков, которые изображены на рис.1. Номера участков, ЭДС источников _и, внутреннее сопротивление источников r_і, сопротивление участков R_i (или сила тока І_і, который протекает по одному из участков в направлении от точки А к В) заданы по вариантам в табл. 1.3.

Найти: 1) величины, указанные в последней колонке таблицы; 2) разность потенциалов между точками А и В.

Пример схемы, которая отвечает 25-му варианту, показанный на рис.1,а.

Задача 1.4 Решить одну из следующих задач (номер задачи указаны в табл. 1.4, рисунки представлены на стр.32).

1 Найти индукцию магнитного поля, которое создается двумя бесконечно длинными проводниками с током. Номер рисунка, на котором показаны расположения проводников, значения силы токов І₁ и І₂, точка, в которой нужно найти магнитную индукцию, и необходимые расстояния заданы в табл. 1.4.

2 Найти напряжённость магнитного поля, которое создается бесконечным прямолинейным проводником и круговым контуром радиуса R. Номер рисунка, на котором показаны расположения проводника и контура, значение силы тока в проводнике І₁ и контуре І₂, точка, в которой надо найти напряженность, и необходимые расстояния заданы в табл. 1.4.

3 По бесконечно длинной согнутой проволоке протекает ток І₁. Номер рисунка, на котором отображена форма проволоки, значение силы тока и необходимые расстояния заданы в табл. 1.4. Найти индукцию магнитного поля в точке О.

4 Бесконечно длинный проводник, согнутый под углом , и круговой контур радиусом R лежат в одной плоскости. Номер рисунка, на котором показаны расположения проводника и контура, значение силы тока в проводнике І₁ и контуре І₂, угол  и необходимые расстояния заданы в табл. 1.4. Найти напряжённость магнитного поля в центре кругового контура.

Задача 1.5 Решить одну из следующих задач (номер задачи указан в табл. 1.5).

1 Заряженная частичка с массой m и зарядом Q влетела в однородное магнитное поле со скоростью υ, которая направлена под углом  к линиям индукции, и движется по винтовой линии. Шаг винтовой линии равен h, радиус равен R. Индукция магнитного поля В. По заданным в табл. 1.5 значениям величин найти величину, которая указана в последней колонке таблицы.

2 Заряженная частичка с массой m и зарядом Q прошла ускоряющую разность потенциалов U и, попав в однородное магнитное поле (магнитная индукция В), движется по окружности радиусом R. По заданным в табл. 1.5 значениям величин найти величину, которая указана в последней колонке таблицы.

3 Заряженная частичка с массой m и зарядом Q, влетая в однородное магнитное поле (магнитная индукция В), движется по окружности, делая один оборот за время Т. По заданным в табл. 1.5 значениям величин найти величину, которая указана в последней колонке таблицы.

Примечание: 1 а.е.м.=1.66·10^–27кг (атомная единица массы); е=1,6·10^–19 Кл (элементарный заряд).

Задача 1.6 Решить одну из следующих задач (номер задачи указан в табл. I.6).

1 Рамка площадью S имеет N витков проволоки сопротивлением R и находится в однородном магнитном поле с индукцией B. Плоскость рамки составляет угол  с линиями магнитной индукции. При изменении направления магнитного поля на противоположное по рамке проходит заряд Q. По значениям величин, заданным в табл. 1.6, найти величину, которая указана в последней колонке таблицы.

2 На соленоид с железным сердечником длиной L и площадью поперечного сечения S надето проволочное кольцо. Обмотка соленоида имеет N витков. При замыкании цепи в обмотке соленоида за время  t устанавливается ток I. При этом в проволочном кольце наводится средняя ЭДС _ср. Магнитная проницаемость железа в этих условиях . По значению величин, заданных в табл. 1.6, найти величину, которая указана в последней колонке таблицы.

3 В однородном магнитном поле с индукцией B вращается короткая катушка, которая имеет N витков диаметром D. Ось вращения лежит в плоскости витков катушки и перпендикулярна линиям индукции магнитного поля. Угловая скорость обращения  (частота обращения , период Т). Максимальное значение ЭДС индукции, которая возникает в катушке _max. По значениям величин, которые заданы в табл. 1.6, найти величину, указанную в последней колонке таблицы.

ТАБЛИЦІ ВАРІАНТІВ ЗАВДАНЬ

Таблиця 1.1

Варіант	Номери задачі	Q1, нКл	Q2, нКл	τ1, нКл/м	τ 2, нКл/м	σ 1, нКл/м2	σ 2, нКл/м2	R, см	l, см	r1, см	r2, см
1	1а	+0.2	–	–	–	+2	+4	–	–	–	–
2	2а	–3	+6	–	–	–	–	6	–	3	10
3	4	–	–	–6	–9	–	–	–	6	6	6
4	5	–	–	–	–	+10	+40	4	10	2	–
5	3	–	–	–2	+3	–	–	5	5	4	–
6	1б	+0.2	–	–	–	–2	–3	–	–	–	–
7	2б	+0.2	–	–	–	–	+3	10	–	1	20
8	4	–	–	+3	+4	–	–	–	5	3	4
9	5	–	–	–	–	–4	–9	6	12	3	–
10	1а	+0.1	–	–	–	+2	–3	–	–	–	–
11	2б	+0.1	–	–	–	–	–10	5	–	3	10
12	3	–	–	+1	+2	–	–	4	5	1	–
13	1б	+0.4	–	–	–	–5	+3	–	–	–	–
14	2а	+1	+5	–	–	–	–	8	–	5	10
15	4	–	–	+10	–5	–	–	–	10	10	10
16	5	–	–	–	–	–6	+8	2	5	1	–
17	4	–	–	–40	–30	–	–	–	5	4	3
18	1а	+0.3	–	–	–	–4	–1	–	–	–	–
19	2а	–2	–4	–	–	–	–	5	–	2	6
20	4	–	–	+8	+4	–	–	–	8	8	8
21	5	–	–	–	–	+4	–6	5	10	4	–
22	3	–	–	–3	–4	–	–	6	3	3	–
23	1б	+0.1	–	–	–	+3	+1	–	–	–	–
24	2б	–0.4	–	–	–	–	–8	8	–	5	10
25	4	–	–	–8	+6	–	–	–	5	4	3
26	1а	–0.4	–	–	–	–2	+4	–	–	–	–
27	3	–	–	+2	–4	–	–	7	5	4
28	2б	–0.5	–	–	–	–	+9	10	–	5	15
29	5	–	–	–	–	–3	–8	4	18	6	–
30	4	–	–	+4	+6	–	–	–	10	4	6

Таблиця 1.2

Варі ант

№за дачі

R1, см

R2, см

L, см

S, см2

d, мм

r, см

ε

Q, нКл

U, В

E, кВ/м

υ, м/с

Знайти

1

1

4

6

–

–

–

5

–

–

–

–

6·106

Q

2

3

–

–

–

100

5

–

–

2

–

–

–



3

4

–

–

–

160

6

–

2,3

9

–

–

–



4

2

1

2

25

–

–

1,5

–

4

–

–

–



5

3

–

–

–

200

5

–

–

–

–

20

–



6

1

1

3

–

–

–

2

–

0,8

–

–

–



7

4

–

–

–

100

8

–

2,7

7

–

–

–



8

3

–

–

–

200

10

–

–

–

200

–

–



9

2

2

4

40

–

–

3

–

–

–

–

2·105

u

10

1

4

5

–

–

–

4,5

–

–

300

–

–



11

3

–

–

–

120

8

–

–

–

–

–

8·106

Q

12

4

–

–

–

200

7

–

4

–

–

50

–



13

1

2

3

–

–

–

2,5

–

–

–

–

107

u

14

2

1,5

2,5

30

–

–

2

–

–

100

–

–



15

3

–

–

–

150

4

–

–

4

–

–

–



16

2

2,5

3,5

45

–

–

3

–

–

–

–

105

Q

17

4

–

–

–

140

10

–

5

–

300

–

–



18

1

2,5

3,5

–

–

–

3

–

2

–

–

–



19

3

–

–

–

100

10

–

–

–

–

–

9·106

u

20

2

1,5

3

35

–

–

2

–

5

–

–

–



21

4

–

–

–

100

4

–

4,5

–

–

–

2·105

Q

22

1

3

4

–

–

–

3,5

–

–

200

–

–



23

2

2

3

30

–

–

2,5

–

–

200

–

–



24

3

–

–

–

150

6

–

–

–

300

–

–



25

4

–

–

–

120

5

–

3,5

–

–

–

3·105

u

26

3

–

–

–

260

3

–

–

–

–

–

2·105

u

27

2

1

3

10

–

–

2

–

–

400

–

–

Q, 

28

3

–

–

–

280

2

–

–

–

–

–

3·105

Q

29

4

–

–

–

290

4

–

6

–

–

–

2·105

u

30

1

5

9

–

–

–

7

–

–

250

–

–

Q

Таблиця 1.3

Варіант	Номери ділянок	εi, В	ri, Ом	Ri, Ом	Іі, А	Знайти
1	1,2,3	ε1 =11, ε2 =4, ε3 =6	r1= r2 = r3 =0	R1 =25, R2 =50, R3 =10	–	І1, І2, І3
2	4,5,6	ε4 =9, ε5 =10	r4 =1, r5 =2	R4 =19, R5 =38	І6 =0,1	І4, І5, R6
3	1,2,4	ε1 =16, ε2 =5, ε4 =7	r1= r2 = r4 =0	R2 =30, R4 =50	І1 =0,4	І2, І4, R1
4	5,4,1	ε1 =9, ε4 =6, ε5 =2	r1= r4 = r5 =0	R4 =50, R5 =10	І1 =0,2	І4, І5, R1
5	1,2,6	ε1 =10, ε2 =8	r1 =2, r2 =1	R1 =8, R2 =19, R6 =60	–	І1, І2, І6
6	3,2,1	ε2 =4, ε3 =5	r1= r2 = r5 =0	R1 =30, R2 =40, R3 =20	І1 =0,1	І2, І3, ε1
7	1,4,6	ε1 =8, ε4 =2	r1 =2, r4 =1	R1 =18, R4 =39, R6 =80	–	І1, І4, І6
8	1,4,2	ε2 =11, ε4 =7	r1= r2 = r4 =0	R1 =50, R2 =20, R4 =30	І1 =0,1	І2, І4, ε1
9	2,1,3	ε1 =9, ε2 =8, ε3 =1	r1= r2 = r5 =0	R1 =50, R2 =20, R3 =10	–	І1, І2, І3
10	4,1,5	ε4 =4, ε5 =2	r1= r4 = r5=0	R1 =25, R4 =50, R5 =10	І1 =0,4	І4, І5, ε1
11	1,3,2	ε2 =16, ε3 =3	r1= r2 = r5 =0	R1 =70, R2 =20, R3 =10	І1 =0,1	І2, І3, ε1
12	6,4,1	ε1 =3, ε4 =7	r1 =2, r4 =1	R1 =78, R4 =39	І6 =0,1	І1, І4, R6
13	5,4,1	ε4 =4, ε5 =14	r1= r4 = r5=0	R1 =90, R4 =20, R5 =40	І1 =0,1	І4, І5, ε1
14	4,6,5	ε4 =10, ε5 =5	r4 =2, r5 =1	R4 =33, R5 =19	І6 =0,3	І4, І5, R6
15	1,6,4	ε1 =4, ε4 =3	r1 =2, r4 =1	R1 =18, R4 =9, R6 =60	–	І1, І4, І6
16	4,1,6	ε1 =2, ε4 =12	r1 =3, r4 =2	R1 =97, R4 =18	І6 =0,1	І2, І4, R6
17	4,1,5	ε1 =22, ε4 =8, ε5 =4	r1= r4 = r5=0	R1 =25, R4 =50, R5 =10	–	І1, І4, І5
18	2,1,6	ε1 =20, ε2 =6	r2 =1	R1 =82, R2 =29, R6 =10	І1 =0,2	І2, І6, r1
19	2,3,1	ε1 =19, ε2 =4, ε3 =5	r1= r2 = r3 =0	R2 =20, R3 =10	І1 =0,2	І2, І3, R1
20	4,1,6	ε1 =13, ε4 =1	r4 =1	R1 =27, R4 =24, R6 =40	І1 =0,3	І4, І6, r1
21	2,1,4	ε1 =12, ε2 =9, ε4 =5	r1= r2 = r4 =0	R1 =30, R2 =60, R4 =20	–	І1, І2, І4
22	2,1,6	ε1 =8, ε2 =6	r1 =3	R1 =27, R2 =9, R6 =25	І2 =0,1	І1, І6, r2
23	5,1,4	ε1 =19, ε4 =6, ε5 =2	r1= r4 = r5=0	R4 =50, R5 =10	І1 =0,2	І4, І5, R1
24	1,6,2	ε1 =18, ε2 =15	r1 =2, r2 =1	R1 =58, R2 =9, R6 =30	–	І1, І2, І6
25	4,1,2	ε2 =4, ε4 =2	r1= r2 = r4 =0	R1 =50, R2 =20, R4 =80	І1 =0,2	І2, І4, ε1
26	1,6,5	ε1 =8, ε5 =6	r1 =2, r5 =3	R1 =8, R5 =12, R6 =10	-	І1, І5, І6
27	2,4,5	ε2 =8	r2 =2, r4 =1, r5 =5	R2 =18, R4 =14, R5 =25	І4=0,2, І5=0,3	І2, ε4, ε5
28	3,6,4	ε3 =36, ε4 =9	r3 =2, r4 =1	R3 =16, R4 =8	І6 =0,5	І4, І3, R6
29	3,1,5	ε3 =40, ε5 =30	r1=r5=2, r3=5	R3 =35, R1 =28, R5 =28	І1 =0,7	І5, І3, ε1
30	2,3,4	ε2=20, ε4=40, ε3=10	r2=10, r4=15, r3 =5	R2 =110, R4 =105	І3 =0,2	І4, І2, R3

Таблиця 1.4

Варіант	Номер задач	Номер рисунка	Точка	І1, А	І2, А	R, см	а, см	b, см	с, см
1	1	2	А	3	4	–	1	–	–
2	3	7	О	10	–	4	–	–	–
3	1	3	А	4	4	–	10	–	–
4	3	10	О	9	–	3	–	–	–
5	2	5	О	10	2	2	5	–	–
6	1	2	В	12	8	–	1	2	–
7	4	11	О	8	5	2	–	–	–
8	1	4	В	8	6	–	5	3	4
9	2	6	В	2	10	5	6	–	–
10	3	8	О	10	–	3	–	–	–
11	1	4	А	5	3	–	8	–	–
12	4	12	О	3	2	4	–	–	–
13	2	6	А	6	5	6	8	–	–
14	3	9	О	8	–	2	–	–	–
15	4	13	О	10	5	5	3	–	–
16	1	2	С	16	12	–	2	4	–
17	3	7	О	5	–	3	–	–	–
18	2	6	О	15	4	4	5	–	–
19	4	11	О	4	3	1	–	–	–
20	1	3	В	6	8	–	5	3	4
21	3	8	О	12	–	2	–	–	–
22	2	5	А	8	10	3	4	–	–
23	4	12	О	6	5	3	–	–	–
24	3	9	О	6	–	1	–	–	–
25	4	13	О	8	2	10	5	–	–
26	1	2	В	2	6	-	5	3	-
27	2	6	B	3	7	5	9	-	-
28	3	10	О	5	-	10	-	-	-
29	1	3	В	3	5	-	5	3	4
30	2	5	А	2	6	7	9	-	-

Таблиця 1.5

Варіант	Номер задачі	m, а.о.м.	Q	В, мТл	U, кВ	, Мм/с	α	R, см	h, см	T, нс	Знайти
1	2	1	е	–	5	–	–	5	–	–	В
2	1	4	–	100	–	0,2	–	4	7	–	Q
3	3	1	е	200	–	–	–	–	–	–	T
4	2	7	е	–	3	–	–	8	–	–	В
5	1	–	–е	2	–	9	–	2	10	–	m
6	3	4	–	400	–	–	–	–	–	652	Q
7	1	1	е	–	–	0,5	–	2	10	–	В
8	2	4	–	100	2	–	–	9,11	–	–	Q
9	3	7	е	300	–	–	–	–	–	–	T
10	1	–	–	3	–	30	–	5	17	–	Q/ m
11	2	–	е	200	0,9	–	–	2,17	–	–	m
12	1	4	2е	500	–	–	–	3	9	–	
13	2	–	–	3	0,8	–	–	3,18	–	–	Q/ m
14	3	–	–е	2	–	–	–	–	–	17,9	m
15	1	1	е	100	–	–	–	6	10	–	
16	2	4	2е	100	4	–	–	–	–	–	R
17	3	7	2е	–	–	–	–	–	–	760	В
18	1	1	е	400	–	2	600	–	–	–	R; h
19	2	7	2е	200	1	–	–	–	–	–	R
20	3	–	–	150	–	–	–	–	–	869	Q/ m
21	1	7	–	400	–	0,3	–	5	13,5	–	Q
22	2	–	–е	5	0,5	–	–	1,5	–	–	m
23	3	–	–	200	–	–	–	–	–	326	Q/ m
24	1	7	2е	500	–	0,6	450	–	–	–	R; h
25	2	4	е	300	–	–	–	5	–	–	U
26	1	3	–	400	–	0,2	–	0,5	1,57	–	,Q
27	1	2	2е	300	–	–	–	1,4	6,3	–	,T
28	2	3	–е	100	–	–	–	6	–	–	U
29	1	4	–2е	–	–	–	–	2	12,5	0,25	,В
30	3	2	2е	–	–	–	–	–	–	30	B

Таблиця 1.6

Варі- ант

Зада- ча

N

S, см2

D, см

L, см

R, Ом

В, Тл

β

Q, мКл

I, A

μ

εср, В

Δt, мс

εмакс, В

ω, 1/с

ν, 1/с

Т, мс

Знай– ти

1

3

–

–

12

–

–

0,4

–

–

–

–

–

–

30

60

–

–

N

2

1

100

80

–

–

20

0,2

30о

-

–

–

–

–

–

–

–

–

Q

3

3

100

–

10

–

–

–

–

–

–

–

–

–

15

90

–

–

В

4

2

500

4

–

30

–

–

–

–

2

–

0,4

2

–

–

–

–

μ

5

1

300

40

–

–

–

0,2

60о

4

–

–

–

–

–

–

–

–

R

6

3

500

–

20

–

–

0,3

–

–

–

–

–

–

90

–

–

–

ω

7

1

400

50

–

–

40

0,1

–

5

–

–

–

–

–

–

–

–

β

8

2

600

4

–

25

–

–

–

–

0,8

400

–

3

–

–

–

–

εср

9

3

300

–

5

–

–

–

–

–

–

–

–

–

50

–

25

–

В

10

1

100

40

–

–

15

–

40о

6

–

–

–

–

–

–

–

–

В

11

3

–

–

18

–

–

0,2

–

–

–

–

–

–

60

–

15

–

N

12

1

200

50

–

–

10

0,3

60о

–

–

–

–

–

–

–

–

–

Q

13

3

100

–

8

–

–

–

–

–

–

–

–

–

80

–

–

20

В

14

2

800

3

–

20

–

–

–

–

0,5

–

0,3

1

–

–

–

–

μ

15

1

–

20

–

–

30

0,3

30о

2

–

–

–

–

–

–

–

–

N

16

3

100

–

8

–

–

0,4

–

–

–

–

–

–

50

–

–

–

Т

17

1

200

20

–

–

5

0,3

–

48

–

–

–

–

–

–

–

–

β

18

3

200

–

20

–

–

0,1

–

–

–

–

–

–

–

–

20

–

εмакс

19

2

700

8

–

40

–

–

–

–

0,6

600

–

2

–

–

–

–

εср

20

3

–

–

15

–

–

0,1

–

–

–

–

–

–

40

–

–

30

N

21

1

500

10

–

–

25

–

20о

4

–

–

–

–

–

–

–

–

В

22

3

200

–

10

–

–

0,2

–

–

–

–

–

–

70

–

–

–

ν

23

2

900

6

–

35

–

–

–

–

–

800

0,6

4

–

–

–

–

I

24

3

400

–

15

–

–

0,3

–

–

–

–

–

–

–

50

–

–

εмакс

25

2

–

5

–

25

–

–

–

–

1

200

0,5

1

–

–

–

–

N

26

2

650

-

–

10

–

–

–

–

0,2

300

0,1

5

–

–

–

–

S

27

3

450

–

–

–

–

0,4

–

–

–

–

–

–

80

–

–

25

D

28

2

150

7

–

15

–

–

–

–

2

200

0,7

-

–

–

–

–

t

29

1

400

-

–

–

5

0,15

70о

6

–

–

–

–

–

–

–

–

S

30

2

900

3

–

-

–

–

–

–

0,4

500

0,2

6

–

–

–

–

L