Приложение а Решения модели Грина-Эмпта

Это приложение обеспечивает различные решения модели Грина-Эмпта проникновения как использующийся калибровать с измерениями. Определение модели было дано в Разделе 4, и отношения модели ко всей модели пролития описаны в Келлере и Симмонсе (2005). Жидкая высота, h, является высотой пролития в каждом местоположении, в то время как это прогрессирует или распространяется по области. Заголовки каждого происхождения ниже относятся к граничным условиям, которые применимые к каждой ситуации, для которой определены параметры проводимости и передней головы. Модель выражена как

где общий напор - h =ho + половина, половина - передняя голова, представляющая капиллярное поглощение, и Хо - прикладной глава. Прикладная голова переменная или с временной зависимостью во многих ситуациях.

1 Решение для Постоянной Головы

При этом условии прикладная главная или высота жидкости считается постоянной, в то время как фронт проникновения продвигается. Тест проникновения этого типа использовался, чтобы оценить проводимость песка (см. Раздел 4.1). С точки зрения безразмерных переменных образцовое уравнение становится

С

Интегрируя получаем:

Когда η маленький относительно 1, последовательное разложение в ряд Тэйлора используется, чтобы получить важное приближение из вышеупомянутого точного решения,

или с точки зрения оригинальных переменных

Это - известный результат, который глубина проникновения продвигает как квадратный корень времени при постоянном прикладном главе. Результат также используется, чтобы получить простое решение или оценку глубины на очень ранних стадиях проникновения.

2 Постоянное Начальное Количество – Уменьшающий Голову

Эти происхождения используются в Секциях 4.1 до 4.4. Для измерения трубы проникновения проводимости жидкости применимое условие - установленная сумма жидкости, которую вылили на поверхности, которую это тогда пропитывает. После того, как жидкое количество введено в трубу проникновения, главные снижения, в то время как проникновение продолжается. Это - “вторая стадия” проникновения, когда жидкое дополнение полное. Когда уровень жидкости повышается, в то время как жидкость применяется, это условие называют первой стадией проникновения. Предположи тогда, что сохранением примененной жидкости дают

где Так постоянное количество жидкости первоначально. Жидкостью, как высота или глубина, является Хо и zo. Уравнение проникновения может тогда быть написано как

С

Интегрируя

Начала на переменных понижены, чтобы упростить примечание. Преобразования между оригинальными переменными, z и t, все еще получим следующее решение:

ηo определен z o. Особый случай держится, когда φ приближается 1. Тогда

который дает

Квадратный корень закона времени получен снова при этом условии.

3 Измененное Постоянное Начальное Количество, чтобы Включать Переднюю Голову

Предшествующиvй случай не включал переднюю голову, которая должна вообще составляться во время проникновения пролития. Это решение просит уменьшающуюся главную или вторую стадию проникновения. Это - происхождение, используемое, чтобы определить проводимость и переднюю голову, соответствуя модели к измерениям проникновения. Отметим, что это - решение, используемое во время каждого временного шага в полной модели пролития, чтобы уменьшить поверхностный уровень, поскольку жидкость распространяется основанный на распространении потока силы тяжести.

Тогда уравнение Грина-Эмпта примет вид:

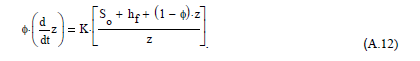
Тогда следующее - преобразования к безразмерным переменным

С

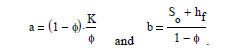
Определили функцию G решения

С

с Решение

Обознгачим F (τ), обозначают обратную функцию G. Это инвертирует G функции, чтобы получить глубину как функцию времени. Решение с точки зрения высоты жидкости вместо глубины может быть дано как

Теперь, когда z = S0 / φ заключительное время, tf, когда проникновение сделано, дают

Когда это заключительное время измерено, вышеупомянутое уравнение определяет ограничение на параметры, a и b. Это решение - основание для того, чтобы найти параметры, K и половину, со второй стадии теста проникновения, во время которого высота, привет, измерена в ряде времен, ti. В t = 0, первая ценность - Хо. Во-первых, a и

b может быть определен, минимизируя сумму квадратов отклонений в h (t) от измерений привет. Таким образом, минимизируй полные брусковые отклонения как

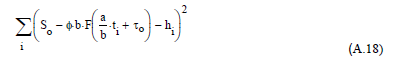
подвергни ограничению, что τo зависит от a и b.