3.2. Соотношения Крамерса-Кронига

Как уже упоминалось в предыдущих параграфах, действительная и мнимая части и комплексной диэлектрической проницаемости, и комплексного показателя преломления (оптические постоянные) не являются независимыми друг от друга. Наиболее общее описание внутренней взаимосвязи между ними в широком интервале частот дается интегральными соотношениями Крамерса-Кронига. Существуют четыре соотношения Крамерса-Кронига для оптических постоянных:

, (3.1.1)

, (3.1.2)

, (3.1.3)

. (3.1.4)

Существует и соотношение Крамерса-Кронига для фазового угла ():

. (3.1.5)

Оно используется как основа метода Крамерса-Кронига для вычисления спектров оптических постоянных из экспериментальных данных об энергетическом коэффициенте отражения (см. ниже параграф 6.1).

Следует подчеркнуть, что интеграл в соотношениях Крамерса-Кронига – это так называемый интеграл в смысле главного значения по Коши.¹³

В соотношениях Крамерса-Кронига (3.1.1)- (3.1.5) фигурируют две частоты, которые следует различать: (а) текущая частота , для которой производится вычисление значения оптической постоянной или функции; (б) частота *, которая служит переменной интегрирования.

Соотношения Крамерса-Кронига определяют численное значение одной оптической постоянной или функции через полный спектр второй оптической постоянной или функции от нуля до бесконечности. Они носят чрезвычайно общий характер и никак не связаны с составом и структурой каких-либо конкретных веществ. Поэтому соотношения Крамерса-Кронига в равной мере применимы к веществам любого состава и в любых агрегатных состояниях. Такая степень общности является не только достоинством, но и причиной недостатка соотношений Крамерса-Кронига: они не дают возможности представить частотную зависимость оптических постоянных в явном виде. Действительно, частотная зависимость одной оптической постоянной определяется только через «черный ящик», каковым является полный спектр второй оптической постоянной, не задаваемый каким-либо конкретным уравнением.

3.3. Описание частотной зависимости оптических постоянных в явном виде: начало истории

Задача отыскания аналитической модели дисперсии показателя преломления, описывающей его частотную зависимость в явном виде, была поставлена практикой еще в девятнадцатом веке. Не останавливаясь на более ранних попытках, обратимся к формуле Зелльмейера, сохраняющей определенное значение до сих пор.

3.3.1. Формула Зелльмейера

Формула Зелльмейера была выведена еще в 1871 г. из физических представлений, достаточно далеких от современных. Ее первоначальный вид таков:

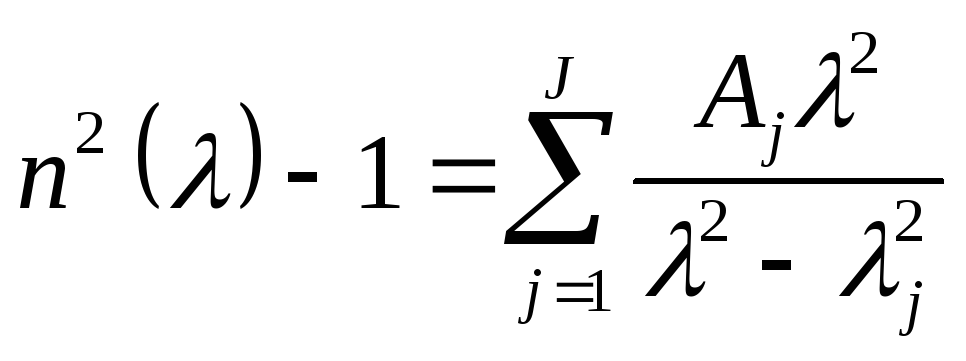, (3.1.6а)

где n() - показатель преломления при длине волны , A_j - константы и _j - эффективные дисперсионные длины волн.

Формула Зелльмейера принимает еще более простой вид путем замены длин волн на частоты:

Отсюда

, (3.1.6б)

где S_j = - константы, имеющие смысл интенсивностей оптических переходов.

Можно видеть, что формула Зелльмейера, в отличие от соотношений Крамерса-Кронига, представляет дисперсию показателя преломления (его зависимость от длины волны или частоты) уже в явном виде, то есть задает значения показателя преломления с помощью вполне конкретной математической функции текущей длины волны или частоты. Поэтому ее постоянные параметры A_j и _j могут быть вычислены из эксперимента, после чего формула Зелльмейера становится пригодной для вычисления показателя преломления при различных длинах волн. Таким образом, формула Зелльмейера явилась первой аналитической моделью дисперсии показателя преломления. Однако она является еще сильно упрощенной. Во-первых, формула Зелльмейера никак не учитывает связь между преломлением и поглощением, отраженную в соотношениях Крамерса-Кронига. Во-вторых, она пригодна лишь в областz[ях, где  > _j или (для части членов суммы)  < _j, так как в точках  =_j правая часть уравнения (3.1.6а) имеет разрывы , где показатель преломления обращается в бесконечность. Тем не менее, для области прозрачности формула Зелльмейера до сих пор с успехом используется в целях точной аппроксимации дисперсии показателя преломления. В частности, один из ведущих мировых производителей оптического стекла – фирма Шотт – приводит дисперсионную формулу типа Зелльмейера для каждой марки своих стекол.

3.3.2. Контур линии поглощения в теории Лоренца

В ранней теории поглощения Лоренца, базировавшейся, как и вывод формулы Зелльмейера, на физических представлениях, еще далеких от современных, экспериментально наблюдаемая форма одиночной линии поглощения описывается следующим образом:

, (3.1.7)

где I() и I₀ – значение интенсивности поглощения при текущей частоте  и пиковое значение интенсивности линии соответственно, ₀ - частота центра линии и  - полуширина линии (ее ширина  на половине высоты, то есть при I() = ½ I₀). Такой контур линии поглощения принято называть лоренцевым (см. рис. 13).

Рис. 13. Общий вид лоренцева контура в области частот его максимума.

С точки зрения физического содержания формула (3.1.7) также является сильно упрощенной. Как и в случае формулы Зелльмейера, она не учитывает связь между поглощением и преломлением. Кроме того, она пригодна лишь в области частот, близких к собственной частоте, то есть при  - ₀ << .