14. Принцип скользящего интерполирования

При восстановлении непрерывного сигнала по дискретному отсчету через конечное число отсчетов проводят полином соответствующей степени. Этот полином в точках отсчетов совпадает со значением отсчета и наз интерполирующий полином.Сначала получают дискретные отсчёты и передают их по линии связи. На приемной стороне восстанавливают его амплитуду, для каждого отсчёта надо сформировать функцию отсчёта и промасштабировоть её с амплитудой дискретного отсчёта. Далее складывают все функции отсчётов и получают непрерывный сигнал. При интерполяции часто используют степенные полиномы, где a_j – постоянные коэфициенты. Если передача идет за время Т_{сигнала}, то степень полинома N=2T_c F_{c max}.

На практике для восстановления непрерывного сигнала в режиме реального времени применяют скользящее интерполирование. От tk берут несколько отсчетов до tk+n и строят интерпол.функцию. n-степень полинома,n+1-количество отсчетов. Интервал, содержащий n+1отсчеты , на котором стоят полином наз. интервалом интерполяции.

Берут N+1 подряд следующих отсчетов, через них проводят полином степени N. На каждом очередном периоде дискретизации из N+1 отсчетов отбрасывают первый и делают очередной отсчет. Через вновь полученные N+1 отсчётов вновь проводят полином степени N. Если N=1, то 2 отсчета просто соединяют линией.

В качестве интерпол. полинома используют полином Лагранжа n-ой степени:

l-интервал соответствия, ui-значение отсчета,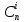-число сочетаний из n по i, i-порядковый номер внутри интервала интерполяции, -относительное время.

Ограничение в степени полинома приводит к погрешности. Она определяется остаточным членом многочлена лагранжа

Для ступенчатой интерполяции: t ,

Для линейной интерполяции t ,

Для параболической 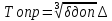t ,

С увеличением порядка полинома, уменьшается погрешность измерения, можно уменьшать частоту опроса и уменьшать требования к быстродействию устройства.

Задержка при восстановлении сигнала минимум 1 период дискретизации.

15. Принцип восстановления непрерывного сигнала по дискретным отсчетам фильтрационным методом.

1. фильтрационный

ФНЧ

Используется ФНЧ с прямоугольным АЧХ. Он сам формирует и складывает функции отсчётов, т. е. если на вход ФНЧ подать последовательность дискретных отсчетов (сигналов с амплитудно-импульсной модуляцией), то на выходе получим непрерывный сигнал, соответствующий моделируемому сигналу.

Исходный сигнал

Восстанавливаем первую составляющую

..вторую

Суммируем то что получилось и в итоге исходный сигнал получаем, но с погрешностью

Т.к. в нулевой спектральной зоне также появляется составляющая сигнала, то можно использовать ФНЧ для ее восстановления.

16. Представление сообщений в цифровой форме. Способы квантование шкалы координат.

Квантование заключается в замене текущего значения дискретного сигнала U (kTопр) одним из конечного числа n уровней.

N=0, 1, 2, ..., N-1

По времени сигнал является дискретным, а по амплитуде непрерывный.

В результате квантования сигнал превращается в цифровой.