1.Виды сигналов. Модели сигналов.
Сигналы, которые точно определены в любой момент времени называются детерминированными сигналами.
U(t)=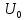
sin(2Пf0t)
t
если значения параметров сигнала предсказать невозможно, то сигнал называется случайным. Случайные изменения могут вызываться либо действиями каким-либо мешающим фактором, либо передаваемым сообщением. В первом случае говорят о действии помех на сигнал, а во втором о модулировании параметра передаваемого сообщения.
Модели сигналов
Модель- это выбранный способ описания процесса или явления, отражающегося существенно с точки зрения решаемой задачи фактора.
По форме представления детерминированный сигнал делят на непрерывные, дискретные и дискретно-непрерывные.
Непрерывный сигнал- это такой сигнал, у которого число возможных значений параметра бесконечны.
Сигнал дискретный по данному параметру, если число значений, которые могут принимать этот параметр конечный.
Сигнал дискретный по одному параметру, а по другому непрерывный, называется дискретно-непрерывным.
4 вида моделей:
1 . непрерывная функция непрерывного
аргумента. 
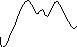
Umax
t
2 . непрерывная функция дискретного
аргумента
U(KT)
t
T 2T 3T 4T 5T
3 . дискретные по m разных
амплитуде уровней и постоянны по времени
Um(t)
t
4 . дискретная функция дискретного аргумента
Um(Kt)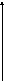
∆U
T 2T 3T t
2.Основные системы базисных функций.
Непрерывный сигнал сложной формы
представляется в виде:
(1), где
-
безразмерный коэффициент,
-базисная
функция. Это обобщенное представление
сигнала или разложение сигнала по
системе базисных функций
.
Требования к базисным функциям: 1) ряд
(1) должен сходиться для любого сигнала,
заданного выражением (1). 2) коэффициенты
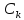должны легко вычисляться 3) значение
коэффициентов не должно зависеть от
верхнего предела суммы в выражении (1).
Система функций
, k=0,1,2..N-1
наз. лин/незав если равенство
(2) справедливо лишь при
для всех k.
Упорядоченность означает, что всегда по некоторому признаку можно определить какая функция является предыдущей, какая последующей.
Система линейно-независимых функций явл. полной если к ней нельзя добавить ни одной новой функции, которая была бы линейно-зависимой по отношению к функциям рассматриваемой системы.
Любую систему неполную базисных функций можно дополнить введение новых функций.
Коэффициенты
Легко вычисляются если в качестве
базисных функций используют систему
ортогональных функций. В общем случае
система базисных функций
,
k=0,1,2, заданных на интервале
наз. Ортогональными, если на этом
интервале выполняется условие:
(3),
-
физический смысл энергии сигнала,
-символ
Кронекера,
=1,
если k=j и
=0,
если не равны.
-
норма базисной функции.
Для действительных функций справедливо (3), но без * (знак комплексного-сопряженного). Система ортогональных базисных функций является частным случаем системы лин/незав функций.
На практике часто используют систему
ортонормированных функций
.
Для перехода от ортогон. к ортонор.
=
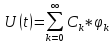
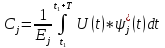(6)
Представление сигнала в виде ряда 1 наз.
обобщенным спектром Фурье. Коэффициенты
,
опред. выраж. (5) и (6) наз обобщенными
коэф. Фурье. Совокупность этих коэффициентов
и порядковых номеров функций наз
обобщенным спектром сигнала
Система
тригонометрических функций:
,
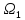-круговая
частота,
,
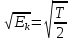
Система комплексных экспоненциальных
функций
, k=..-2,-1,0,1,2..
Полиномы Лежандре. Они ортогональны на отрезке [-1;1] с единичной весовой функцией h=1
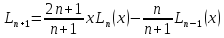(слева рисунок)
,
,
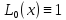Функции Уолша.(справа рисунок) Система
функций {wali(Θ)}
является расширенной системой функций
Родемахера до полной и определяется
след образом: нулевая функция =1,
,i-номер
функции.
Функции Родемахера r0(
)=1,
ri(
)=sign(sin(2π
)),
Функции Уолша- кусочно-непрерывные
ступенчатые функции принимающие на
области определения 2 дискретных значения
1 и -1. Они являются ортогональными на
области определения аргумента [0.1]
Функции Хаара- полная ортонормированная
система функций на интервале
,
Har10 – 1 группа и 0 функция.
Применяются для выделения QRS сегмента.