6.2.2. Апроксимація перехідної характеристики ланцюжком однакових аперіодичних ланок

Об`єкти керування, що мають S-образні перехідні характеристики зручно описувати передаточною функцією виду:

(6.20)

Визначенню підлежать параметри Т і n ( k – визначається на попередньому етапі).

Вихідні дані для розрахунків ті ж що і у випадку апроксимації аперіодичною ланкою 1-го порядку.

Функцію W(p) розкладують в ряд за степенями р по формулі Ньютона:

, (6.21)

де А₁= nT; .

Використовуючи експериментальну перехідну характеристику обчислюють S и S₁ за формулами:

(6.22)

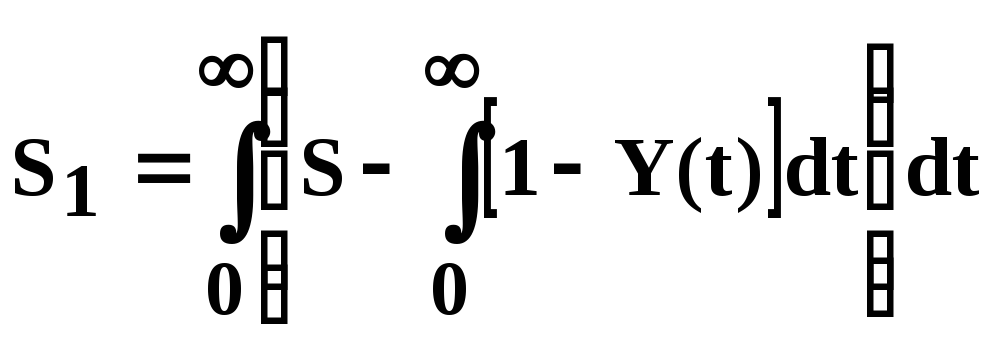
Коефіцієнти А₁ и А₂ є аналогами S и S₁. Тому на основі виразів (6.21) – (6.22) можна записати:

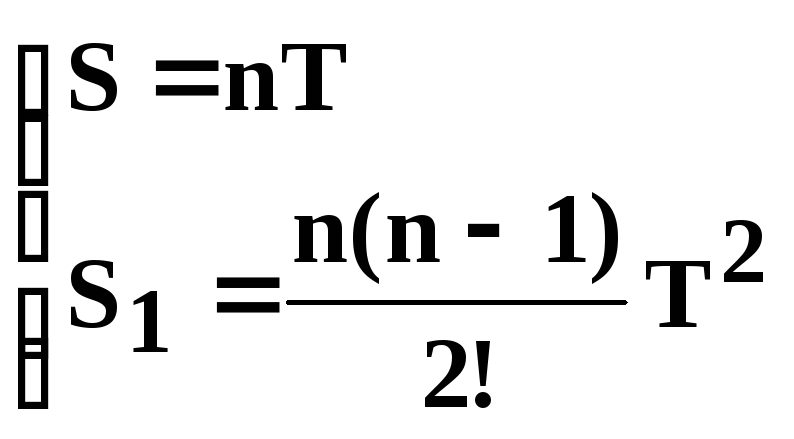(6.23)

Звідки

(6.24)

Оскільки по визначенню n є цілим числом, то

(6.25)

де int(a) – найбільше ціле до а число, що не перевищує його.

Обчислені за (6.24) значення n и Т є початковими для пошуку їхніх оптимальних значень, тобто таких, при яких досягався мінімум критерію І (6.19).

Апроксимуюча перехідна характеристика розраховується за формулою:

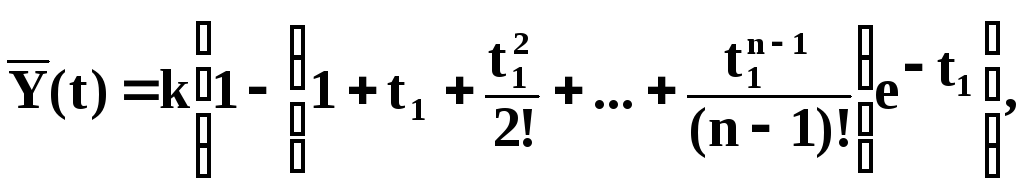(6.26)

де

Мінімум функції І визначається шляхом варіювання n з кроком 1. Спочатку n збільшують. Якщо просування у цьому напрямку призводить до зменшення І, то n продовжують збільшувати до першого невдалого кроку. Потім здійснюється повернення на один крок і відповідне йому значення Т и n вважаються оптимальними.

6.2.3. Апроксимація перехідної характеристики аперіодичною ланкою другого порядку і ланкою запізнювання.

Структура передаточної функції об`єкта має вигляд (6.9).

Вихідними даними для апроксимації є перехідна характеристика об`єкта, яка задана у виді ординат із сталим кроком.

Коефіцієнт передачі об`єкта визначається на попередньому етапі.

Сума S сталих часу та часу запізнювання у функції (6.9) дорівнює площі між нормованою перехідної характеристикою та лінією її усталеного значення.

Величина S обчислюється численним методом і повідомляється користувачеві. Користувач розподіляє S між окремими сталими часу и вводить значення .

Програма обчислює нормовану перехідну характеристику і виводить на екран дисплея графіки експериментальної і розрахункової характеристики. На екран виводиться також точність апроксимації І, що обчислюється за формулою (6.19).

Користувач оцінює результат апроксимації і приймає рішення про закінчення роботи, або продовжує обчислення для інших варіантів розподілу S.

6.2.4. Апроксимація перехідної характеристики методом Симою

Метод Симою є універсальним методом апроксимації, що дозволяє отримати апроксимуючі вирази будь-якого порядку. Цей метод дуже зручний для обробки на ЕОМ, він легко алгоритмізується та відрізняється великою точністю.

Апроксимуючою залежністю є дробно-раціональна передаточна функція виду:

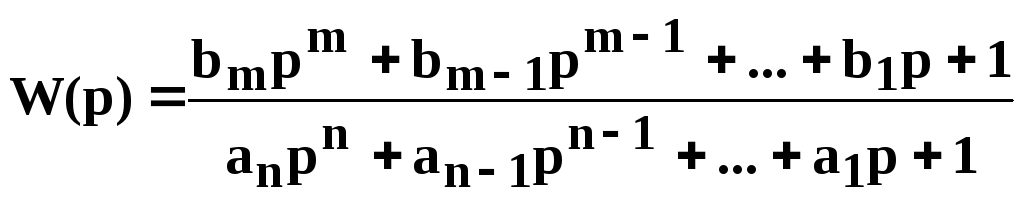(6.27)

Невідомі коефіцієнти визначають із наступної системи рівнянь:

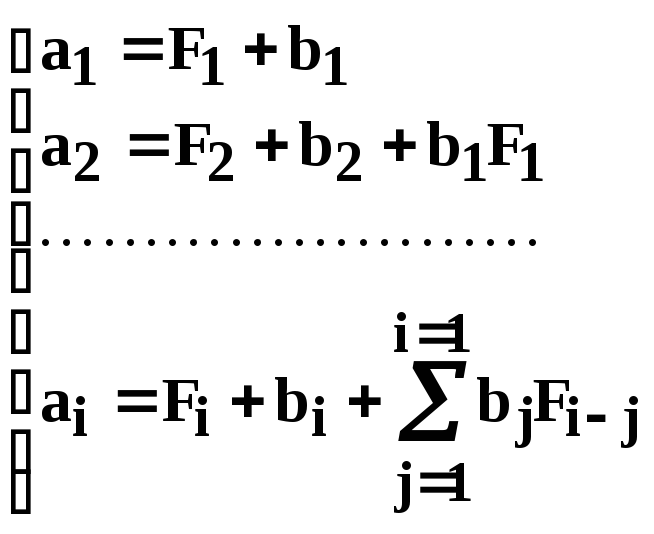(6.28)

Коефіцієнти в системі рівнянь (6.28) розраховується по формулам:

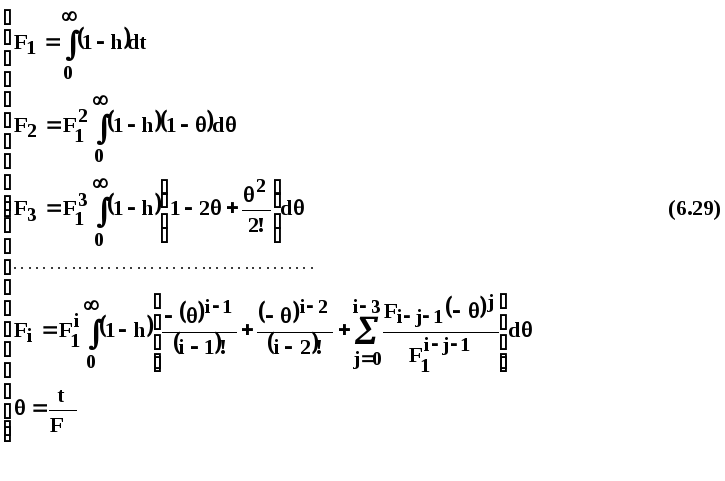
Коефіцієнти зв`язані з перехідною характеристикою інтегральними залежностями ( Див. рис. 6.3)

h(t)

1

t

Рисунок 6.3 - Зв`язок коефіцієнта з перехідною характеристикою.