
- •Колебания и волны лабораторный практикум
- •Работа № 20а
- •Свободные колебания физического маятника
- •Дифференциальное уравнение колебаний физического маятника
- •Определение момента инерции маятника по измерениям периодов колебаний
- •Описание экспериментальной установки
- •Задание к работе
- •Контрольные вопросы
- •Нормальные колебания первого (синфазного) типа
- •Нормальные колебания второго (противофазного) типа
- •Нормальные координаты
- •Явление биений
- •Измерение частот колебаний
- •Задание к лабораторной работе
- •Контрольные вопросы
- •2. Сложение двух взаимно перпендикулярных гармонических колебаний
- •Описание экспериментальной установки
- •Задание к работе
- •Описание лабораторной установки и методики измерений
- •Задание к работе
- •Контрольные вопросы
- •Описание установки
- •Задание к работе
- •Контрольные вопросы
- •Описание лабораторной установки
- •Задание к работе
- •Контрольные вопросы
- •Литература
Описание установки
В
лабораторной установке (см. схему на
рис. 1) напряжение на конденсаторе
измеряется вольтметром в положении 2
переключателя; в положении 1 вольтметр
подключается непосредственно к
генератору, являющемуся источником
переменной ЭДС регулируемой частоты.
Вольтметр, обладающий большим внутренним
сопротивлением, позволяет измерять
переменные напряжения в широком интервале
частот. Чтобы исключить влияние
внутреннего сопротивления генератора
![]() на измеряемые величины напряжений,
необходимо выполнить соотношение
на измеряемые величины напряжений,
необходимо выполнить соотношение
![]() .
В этом случае в положении 1 переключателя
показания вольтметра практически
соответствуют величине
.
В этом случае в положении 1 переключателя
показания вольтметра практически
соответствуют величине
![]() .
.
Задание к работе
-
Ознакомиться в лаборатории с инструкцией по пользованию приборами установки.
-
Рассчитать
 и ее погрешность по исходным данным
установки.
и ее погрешность по исходным данным
установки. -
При заданных значениях
 ,
изменяя частоту выходного напряжения
генератора и поддерживая постоянное
значение амплитуды его напряжения (по
указанию преподавателя), снять частотные
характеристики напряжения на конденсаторе.
Особо тщательно проводить измерения
вблизи резонансных частот (для этого,
используя расчеты п. 2, вначале
определить экспериментально эти частоты
грубо).
,
изменяя частоту выходного напряжения
генератора и поддерживая постоянное
значение амплитуды его напряжения (по
указанию преподавателя), снять частотные
характеристики напряжения на конденсаторе.
Особо тщательно проводить измерения
вблизи резонансных частот (для этого,
используя расчеты п. 2, вначале
определить экспериментально эти частоты
грубо). -
В общих осях построить графики зависимости
 от частоты для различных R.
Определить по графикам
от частоты для различных R.
Определить по графикам
 резонансные
частоты. Сравнить их с расчетными с
учетом погрешностей.
резонансные
частоты. Сравнить их с расчетными с
учетом погрешностей. -
По графикам
 ,
пользуясь формулой
,
пользуясь формулой
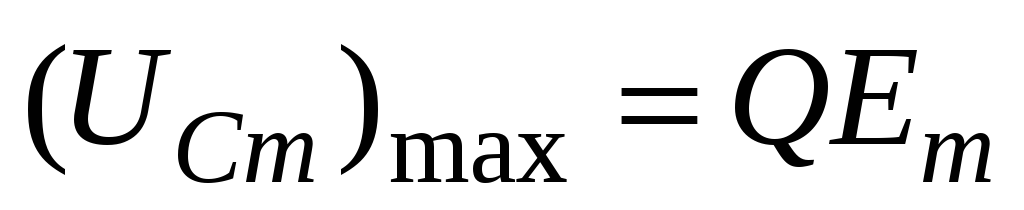 ,
найти добротность
,
найти добротность
 контуров при использованных значениях
контуров при использованных значениях
 .
. -
Сделать выводы относительно: изменения
 и
и
 в зависимости от сопротивления,
включенного в контур; высоты максимумов
кривых при разных сопротивлениях; а
также совпадения между резонансными
частотами: найденными экспериментально
и вычисленными.
в зависимости от сопротивления,
включенного в контур; высоты максимумов
кривых при разных сопротивлениях; а
также совпадения между резонансными
частотами: найденными экспериментально
и вычисленными.
Контрольные вопросы
-
Какие колебания называются вынужденными?
-
Что такое резонанс напряжений на конденсаторе в контуре?
-
Нарисуйте принципиальную схему установки. Для чего необходимо регулярно проверять, удерживается ли первоначально заданное выходное напряжение генератора?
-
Напишите дифференциальное уравнение вынужденных колебаний. Записать и проанализировать частное решение этого уравнения.
-
Получить выражение для амплитуды колебаний напряжения на конденсаторе (выражение (8)).
-
Найти резонансную частоту для
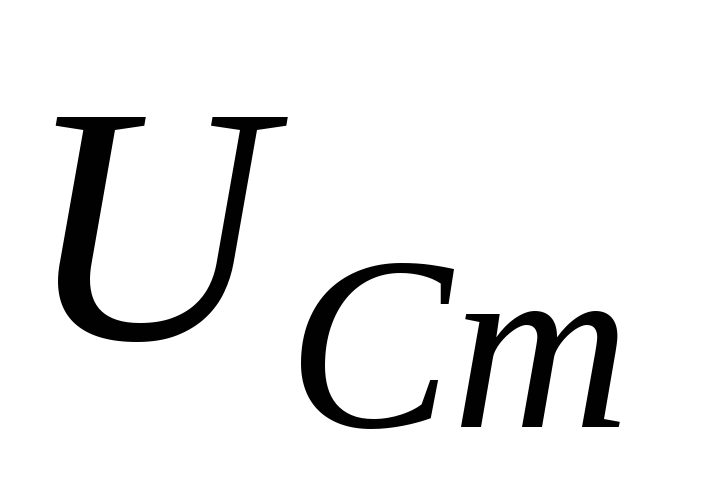 .
. -
Получить выражение для амплитуды колебаний тока в цепи и найти резонансную частоту для
 .
. -
Как вычислить
 и
и
 ?
? -
Какой график вы будете строить в работе? Какой он будет иметь вид? Проходит ли он через начало координат?
-
Как сдвигается резонансная частота при увеличении сопротивления контура?
-
Что такое добротность
 колебательного контура?
колебательного контура? -
Получили ли вы то, что ожидали?
-
Привести примеры применения резонанса в технике.
Литература
-
Трофимова Т.И. Курс физики. – М.: Академия, 2004 (и др. годы изданий).
-
Савельев И.В. Курс общей физики. – М.: Астрель, 2001 (и др. годы изданий).
Работа № 24
ВОЛНЫ НА СТРУНЕ
Цель работы: экспериментально определить зависимости собственных частот струны от силы ее натяжения и от номера гармоники и сравнить с зависимостями, рассчитанными теоретически.
Волновое уравнение струны и его решение
Уравнение
любой волны является решением
дифференциального уравнения, называемого
волновым уравнением. Для струны, вытянутой
вдоль оси
![]() ,
отдельные точки которой совершают
колебания вдоль оси
,
отдельные точки которой совершают
колебания вдоль оси
![]() ,
это уравнение имеет вид
,
это уравнение имеет вид
![]() ,
(1)
,
(1)
где
![]() –
скорость распространения волны (фазовая
скорость). Это уравнение можно получить
из второго уравнения Ньютона, записанного
для произвольного, достаточно малого
элемента струны, показанного на рис. 1.
–
скорость распространения волны (фазовая
скорость). Это уравнение можно получить
из второго уравнения Ньютона, записанного
для произвольного, достаточно малого
элемента струны, показанного на рис. 1.

Рис. 1
Уравнение
получим в предположении малости углов
![]() .
При малых углах
.
При малых углах
![]() длину рассматриваемого элемента можно
считать равной
длину рассматриваемого элемента можно
считать равной
![]() ,
а массу
,
а массу
![]() – равной
– равной
![]() ,
где
,
где
![]() –
линейная плотность струны. Этот элемент
совершает колебания вдоль оси
–
линейная плотность струны. Этот элемент
совершает колебания вдоль оси
![]() .
В этом направлении на элемент струны
действует сила, равная
.
В этом направлении на элемент струны
действует сила, равная

Эта сила вызывает ускорение

![]() ,
,
откуда следует волновое уравнение
![]() .
(2)
.
(2)
Из сравнения уравнений (1) и (2) видно, что фазовая скорость волны, распространяющейся вдоль струны,
![]() .
(3)
.
(3)
Любая функция, удовлетворяющая уравнению (1), описывает некоторую волну. Вдоль бесконечно длинной струны могут распространяться гармонические волны, описываемые уравнением
![]() ,
(4)
,
(4)
если
волна распространяется вдоль оси
![]() в положительном направлении, и уравнением
в положительном направлении, и уравнением
![]() ,
(5)
,
(5)
если волна распространяется в отрицательном направлении.
В
том, что выражения (4) и (5) являются
решением волнового уравнения (1), можно
убедиться подстановкой этих выражений
в волновое уравнение. Частота колебаний
![]() при этом может иметь любое значение.
Эта частота определяется частотой
источника, возбуждающего колебания
струны.
при этом может иметь любое значение.
Эта частота определяется частотой
источника, возбуждающего колебания
струны.
Уравнение, представляющее собой сумму выражений (4) и (5):
![]() ,
,
также является решением волнового уравнения. Это выражение можно привести к виду
![]() .
(6)
.
(6)
Волна,
описываемая таким уравнением, называется
стоячей. В каждой точке стоячей волны
колебания происходят с той же частотой,
что и у встречных волн. Амплитуда
колебаний зависит от координаты
![]() :
:
![]() =
=
![]() .
(7)
.
(7)
Для
струны конечной длины с закрепленными
концами амплитуда результирующего
колебания на концах струны должна
равняться нулю. Если начало струны
находится в точке с координатой
![]() ,
то амплитуда в этой точке будет равна
нулю в том случае, когда
,
то амплитуда в этой точке будет равна
нулю в том случае, когда
![]() .
Выражение (7) при этом будет иметь вид
.
Выражение (7) при этом будет иметь вид
![]() .
(8)
.
(8)
На
конце струны, в точке с координатой
![]() ,
где
,
где
![]() –
длина струны, амплитуда также должна
равняться нулю. Для этого должно
выполняться условие
–
длина струны, амплитуда также должна
равняться нулю. Для этого должно
выполняться условие
![]()
![]() .
.
Из
последнего выражения следует, что
стоячие волны на струне могут существовать
только на таких частотах
![]() ,
для которых длина волны
,
для которых длина волны
![]()
![]() .
(9)
.
(9)
Частота
колебаний связана с длиной волны
соотношением
![]() ,
где
,
где
![]() –
фазовая скорость волны. Тогда с учетом
выражения (3) частоты
–
фазовая скорость волны. Тогда с учетом
выражения (3) частоты
![]() могут быть определены по формуле
могут быть определены по формуле
 .
(10)
.
(10)
В
теории колебаний эти частоты называют
гармониками (первая гармоника, вторая
гармоника и т. д.) В музыкальной
акустике первую гармонику называют
основным тоном. Гармоники более высоких
порядков называют обертонами. Частоты
![]() называют также собственными частотами
колебаний струны.
называют также собственными частотами
колебаний струны.
Зависимость
амплитуды колебаний
![]() от координаты
от координаты
![]() для различных номеров гармоник
для различных номеров гармоник
![]() может быть представлена выражением
может быть представлена выражением
![]() .
(11)
.
(11)
или с учетом соотношения (9) – выражением
![]() .
(12)
.
(12)
Из
выражения (12) следует, что амплитуда
равна нулю в тех точках струны, для
которых
![]() принимает целочисленное или
нулевое
значение. Так для первой гармоники таких
точек две, с координатами
принимает целочисленное или
нулевое
значение. Так для первой гармоники таких
точек две, с координатами
![]() и
и
![]() ,
т.е. на концах струны. Для второй гармоники
таких точек три: на концах струны и в
точке
,
т.е. на концах струны. Для второй гармоники
таких точек три: на концах струны и в
точке
![]() ,
т.е. в середине струны. Для третьей
гармоники – четыре точки: на концах
струны и в точках с координатами
,
т.е. в середине струны. Для третьей
гармоники – четыре точки: на концах
струны и в точках с координатами
![]() и
и
![]() .
.
Точки,
амплитуды колебаний в которых равны
нулю, называют узлами стоячей волны.
Расстояние между соседними узлами
![]() называют длиной стоячей волны. Из
выражения (11) следует, что минимальное
расстояние между узлами равно половине
длины бегущей волны. Следовательно,
называют длиной стоячей волны. Из
выражения (11) следует, что минимальное
расстояние между узлами равно половине
длины бегущей волны. Следовательно,
![]() .
На длине струны укладывается целое
число полуволн бегущей волны и
соответственно целое число длин волн
стоячей волны, численно равное номеру
гармоники
.
На длине струны укладывается целое
число полуволн бегущей волны и
соответственно целое число длин волн
стоячей волны, численно равное номеру
гармоники
![]() .
Точки, в которых амплитуда достигает
максимального значения, называются
пучностями стоячей волны. Число пучностей,
укладывающихся на длине струны, также
равно
.
Точки, в которых амплитуда достигает
максимального значения, называются
пучностями стоячей волны. Число пучностей,
укладывающихся на длине струны, также
равно
![]() .
.
На
рис. 2 показана зависимость смещения
точек струны
![]() от координаты
от координаты
![]() на частоте второй гармоники для трех
моментов времени:
на частоте второй гармоники для трех
моментов времени:
![]() (кривая 1);
(кривая 1);
![]() ,
где
,
где
![]() –
период колебаний (кривая 2);
–
период колебаний (кривая 2);
![]() (кривая 3).
(кривая 3).
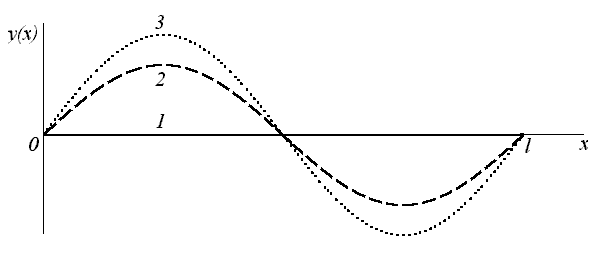
Рис. 2
Видно,
что точки струны между соседними узлами
движутся в одинаковой фазе. Однако точки
струны, расположенные по разные стороны
узла на расстоянии, меньшем
![]() ,
движутся в противофазе.
,
движутся в противофазе.
Рассмотрим теперь способы возбуждения стоячих волн на струнах. В большинстве струнных музыкальных инструментов для этого используется либо удар по струне специальным молоточком (рояль, пианино), либо рывок (гитара и другие щипковые инструменты). Во всех этих случаях зависимость возбуждающей силы от времени не является гармонической, а имеет вид кратковременного импульса. Однако любой кратковременный импульс можно представить как сумму бесконечно большого числа гармонических функций в бесконечно большом диапазоне частот. Те составляющие, частоты которых совпадают с частотами, определяемыми формулой (10), возбуждают стоячие волны. Одновременно возбуждаются как основной тон, так и все его обертоны. Самую большую интенсивность имеет звук основного тона. На обертоны приходится лишь незначительная доля энергии. Соотношение между интенсивностями основного тона и каждого из обертонов определяет тембр звука. Это соотношение для разных инструментов разное. Поэтому разные инструменты, настроенные на одну и ту же частоту основного тона, звучат по-разному.
В настоящей работе струна возбуждается силой, изменяющейся по гармоническому закону. Для этого используется металлическая струна, к концам которой подводится переменное электрическое напряжение от генератора звуковой частоты. Часть струны проходит через зазор между полюсами электромагнита, питаемого от источника постоянного тока. На эту часть струны действует сила Ампера в направлении, перпендикулярном длине струны и силовым линиям магнитного поля. Эта сила изменяется по гармоническому закону с частотой, задаваемой на генераторе. Колебания струны могут возбуждаться только в том случае, если частота электрических колебаний генератора совпадает с частотой какой-либо одной из гармоник. Следовательно, рассмотренным способом можно возбудить любые гармоники, но только по отдельности. Для эффективного возбуждения колебаний струны магнит должен быть расположен так, чтобы между полюсами магнита находилась пучность стоячей волны.
В отличие от бегущей волны в стоячей волне не происходит переноса энергии вдоль струны. Поэтому в случае отсутствия потерь энергии даже при кратковременном импульсном возбуждении струна должна колебаться бесконечно долго. Однако реально всегда существуют потери энергии (например, на излучение звука) и колебания являются затухающими. При возбуждении струны силой, изменяющейся по гармоническому закону (от генератора электрических колебаний), колебания являются вынужденными. В установившемся режиме они происходят с частотой вынуждающей силы, и амплитуда колебаний со временем не меняется. Потери энергии компенсируются энергией, поступающей от генератора.
