
Вынужденые колебания с учётом силы сопртивления движению
Из условий статического равновесия рис 1в имеем:

Тогда
![]() .
.
Из начальных условия рис 1б имеем:

Рассматривая динамическую расчетную схему (рис. 3, г) по закону Ньютона запишем:
![]()

![]()
![]()
![]()
После выполнения сокращений уравнение приводим к каноническому виду:
![]() ,
,
![]()
Рассмотрим случай когда k > n
где
![]() ,
k – собственная
частота колебаний груза на пружине.
,
k – собственная
частота колебаний груза на пружине.
![]()
Решение неоднородного дифференциального уравнения второго порядка
имеет вид:
![]()
где х1 – общее решение соответствующего однородного уравнения
![]() ,
,
![]()
х2 – частное решение неоднородного уравнения, вид которого определяется видом правой части уравнения в общем случае.
![]()
где А и В – некоторые постоянные, значения которых определяются подстановкой частного решения х2 в неоднородное дифференциальное уравнение.

Для того, чтобы равенство выполнялось при любом значении ψ коэффициенты при sin ψ и при cos ψ в левой и правой частях этого уравнения должны быть равны.
![]()
Возведем в квадрат, а потом сложим последние уравнения

Тогда
![]()
Тепер решение дифференциального уравнения отыскиваем в виде:
![]()
Определим неизвестные постоянные интегрирования С1 и С2 , для этого необходимо продифференцирывать последнее выражение

Используем начальные условия задачи:
1) При t = 0
![]() ,
т.е
,
т.е
![]()
2) При t = 0
![]() ,
т.е.
,
т.е.
 Подставим
найденные численные значения коэффициентов.
Окончательно получим:
Подставим
найденные численные значения коэффициентов.
Окончательно получим:
![]()
Рассмотрим случай когда k = n
![]()
Решение неоднородного дифференциального уравнения второго порядка
имеет вид:
![]()
где х1 – общее решение соответствующего однородного уравнения
![]() ,
,
![]()
х2 – частное решение неоднородного уравнения, вид которого определяется видом правой части уравнения в общем случае.
![]()
где А и В – некоторые постоянные, значения которых определяются подстановкой частного решения х2 в неоднородное дифференциальное уравнение.

Для того, чтобы равенство выполнялось при любом значении ψ коэффициенты при sin ψ и при cos ψ в левой и правой частях этого уравнения должны быть равны.
![]()
Возведем в квадрат, а потом сложим последние уравнения

Тогда
![]()
Тепер решение дифференциального уравнения отыскиваем в виде:
![]()
Определим неизвестные постоянные интегрирования A1 и A2 , для этого необходимо продифференцирывать последнее выражение
![]()
Используем начальные условия задачи:
1) При t = 0
![]() ,
т.е
,
т.е
![]()
2) При t = 0
![]() ,
т.е.
,
т.е.
![]()
Подставим найденные численные значения коэффициентов. Окончательно получим:
![]()
Рассмотрим случай когда k < n
![]()
Решение неоднородного дифференциального уравнения второго порядка
имеет вид:
![]()
где х1 – общее решение соответствующего однородного уравнения
![]()
![]()
х2 – частное решение неоднородного уравнения, вид которого определяется видом правой части уравнения в общем случае.
![]()
где А и В – некоторые постоянные, значения которых определяются подстановкой частного решения х2 в неоднородное дифференциальное уравнение.

Для того, чтобы равенство выполнялось при любом значении ψ коэффициенты при sin ψ и при cos ψ в левой и правой частях этого уравнения должны быть равны.
![]()
Возведем в квадрат, а потом сложим последние уравнения
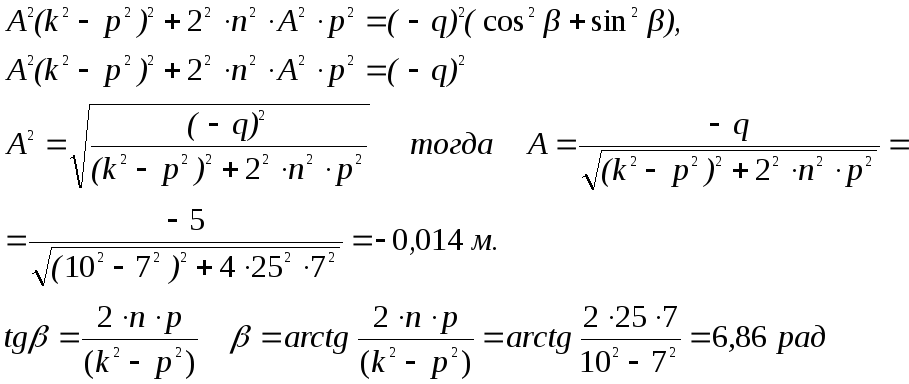
Тогда
![]()
Тепер решение дифференциального уравнения отыскиваем в виде:
![]()
Определим неизвестные постоянные интегрирования A1 и A2 , для этого необходимо продифференцирывать последнее выражение

Используем начальные условия задачи:
1) При t = 0
![]() ,
т.е
,
т.е
![]() ,откуда
,откуда
![]()
2) При t = 0
![]() ,
т.е.
,
т.е.
![]() ,
откуда
,
откуда
 Подставим
найденные численные значения коэффициентов.
Окончательно получим:
Подставим
найденные численные значения коэффициентов.
Окончательно получим:
![]()
