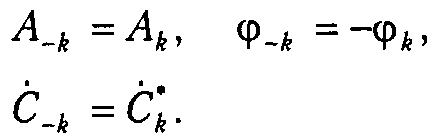5. Сигнали з кінцевою енергією та їхні енергетичні характеристики.

Энергия сигналов может быть конечной или бесконечной. Конечную энергию имеют финитные сигналы и сигналы, затухающие по своим значениям в пределах конечной длительности, которые не содержат дельта-функций и особых точек (разрывов второго рода и ветвей, уходящих в бесконечность). В противном случае их энергия равна бесконечности. Бесконечна также энергия периодических сигналов.

Для множества сигналов с ограниченной энергией должно выполняться условие:

L₂ = {s; |s(t)|² dt < ∞}.

О сигналах s(t) данного множества принято говорить, что они интегрируемы с квадратом. Очевидно, что этому множеству могут соответствовать только сигналы, стремящиеся к нулю на бесконечности: s(t) → 0.

Как правило, к этому типу сигналов относятся апериодические и импульсные сигналы, не имеющие разрывов 2-го рода при ограниченном количестве разрывов 1-го рода. Любые периодические, полигармонические и почти периодические сигналы, а также сигналы с разрывами и особыми точками 2-го рода, уходящими в бесконечность, относятся к сигналам с бесконечной энергией. Для их анализа применяются специальные методы.

6. Сигнали з нескінченною енергією та їхні енергетичні характеристики.

Для бесконечных по энергии сигналов, в том числе для периодических, ограничение по энергии может задаваться для определенного интервала (периода) T = t1-t2:

L₂(T) = {s;|s(t)|² dt < ∞}.

Иногда в отдельный класс выделяют сигналы конечной длительности, отличные от нуля только на ограниченном интервале аргументов (независимых переменных). Такие сигналы называют финитными.

7. Ряд Фур’є та його форми представлення. (№ 8+9)

Разложению в ряд Фурье могут подвергаться периодические сигналы. При этом они представляются в виде суммы гармонических функций либо комплексных экспонент с частотами, образующими арифметическую прогрессию. Для того чтобы такое разложение существовало, фрагмент сигнала длительностью в один период должен удовлетворять условиям Дирихле:

□ не должно быть разрывов второго рода (с уходящими в бесконечность ветвя­ми функции);

□ число разрывов первого рода (скачков) должно быть конечным;

□ число экстремумов должно быть конечным (в качестве примера функции, ко­торая на конечном интервале имеет бесконечное число экстремумов, можно привести sin(1/x) в окрестности нуля).

В зависимости от конкретной формы базисных функций различают несколько форм записи ряда Фурье.

ЗАМЕЧАНИЕ -

Ряд Фурье может быть применен для представления не только периодических сигналов, но и сигналов конечной длительности. При этом оговаривается временной интервал, для которого строится ряд Фурье, а в остальные моменты времени сигнал считается равным нулю. Для расчета коэффициентов ряда такой подход фактически означает периодическое продолжение сигнала за границами рассматриваемого интервала.

Синусно-косинусная форма

В этом варианте ряд Фурье имеет следующий вид:

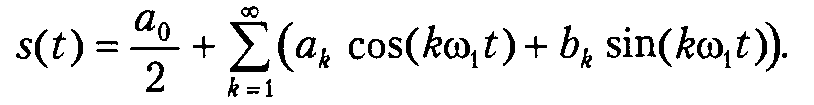Здесь = 2pi/Т — круговая частота, соответствующая периоду повторения сиг­нала, равному Т. Входящие в формулу кратные ей частоты кназываются гар­мониками; гармоники нумеруются в соответствии с индексом к; частота = к называется к-й гармоникой сигнала. Коэффициенты ряда а_к и в_к рассчитываются по формулам:

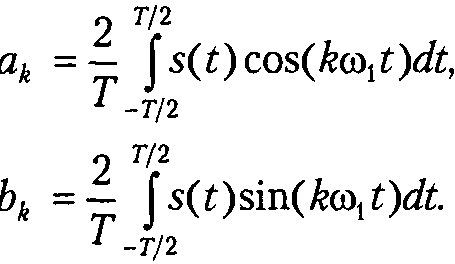Константа а₀ рассчитывается по общей формуле для а_k. Ради этой общности и введена несколько странная на первый взгляд форма записи постоянного слагае­мого (с делением на два). Само же это слагаемое представляет собой среднее значение сигнала на периоде:

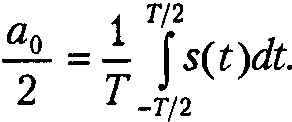Если s(t) является четной функцией, то все b_к будут равны нулю и в формуле ряда Фурье будут присутствовать только косинусные слагаемые. Если s(t) является нечетной функцией, равны нулю будут, наоборот, косинусные коэффициен­ты а_k и в формуле останутся лишь синусные слагаемые.

Вещественная форма

некоторое неудобство синусно-косинусной формы ряда Фурье состоит в том, что для каждого значения индекса суммирования k (то есть для каждой гармони­ки с частотой кw₁) в формуле фигурируют два слагаемых — синус и косинус. Воспользовавшись формулами тригонометрических преобразований, сумму этих двух слагаемых можно трансформировать в косинус той же частоты с иной ам­плитудой и некоторой начальной фазой:

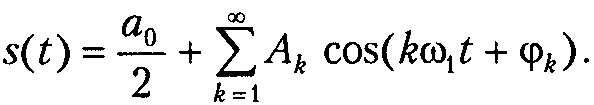Если s(t) является четной функцией, фазы могут принимать только значе­ния 0 и pi, а если s(t) — функция нечетная, то возможные значения для фазы рав­ны ±pi/2.

Комплексная форма

Данная форма представления ряда Фурье является, пожалуй, наиболее употре­бимой в радиотехнике. Она получается из вещественной формы представлением косинуса в виде полусуммы комплексных экспонент (такое представление выте­кает из формулы Эйлера е^jx = cos x+j sin x):

Применив данное преобразование к вещественной форме ряда Фурье, получим суммы комплексных экспонент с положительными и отрицательными показате­лями:

А теперь будем трактовать экспоненты со знаком «минус» в показателе как чле­ны ряда с отрицательными номерами. В рамках этого же общего подхода посто­янное слагаемое а₀/2 станет членом ряда с нулевым номером. В результате полу­чится комплексная форма записи ряда Фурье:

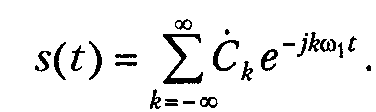
Комплексные коэффициенты ряда связаны с амплитудами А_к и фазами , фигу­рирующими в вещественной форме записи ряда Фурье.(1.7), следующими не­сложными соотношениями:

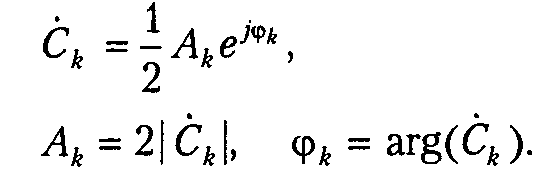
Несложно выглядят и формулы связи с коэффициентами а_к и Ь_к синусно-косинусной формы ряда Фурье (1.6):

Отсюда сразу же следует и формула непосредственного расчета коэффициентов С_к ряда Фурье в комплексной форме:

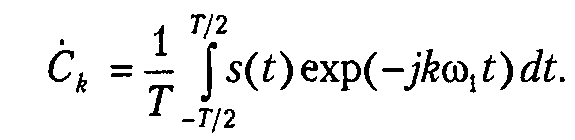
Если s(t) является четной функцией, коэффициенты ряда С_k будут чисто веще­ственными, а если — функция нечетная, коэффициенты ряда окажутся чис­то мнимыми.

Совокупность амплитуд гармоник ряда Фурье часто называют амплитудным спектром, а совокупность их фаз — фазовым спектром. Эти понятия не следует путать с амплитудно- и фазочастотными характеристиками, которые относятся не к сигналам, а к цепям. Если анализируемый сигнал s(t) является вещественным, то его амплитудный и фазовый спектры обладают симметрией: