
- •Смоленск, 2010 Содержание:
- •Задание на расчет.
- •Числовые данные:
- •I. Описание работы системы.
- •II. Составление дифференциальных уравнений движения звеньев.
- •III. Коэффициенты передачи.
- •IV.Критерии устойчивости системы.
- •V. Исследование статической ошибки.
- •VI.Частотные характеристики.
- •VII. Выходная величина и ошибка регулирования.
- •Литература.
III. Коэффициенты передачи.
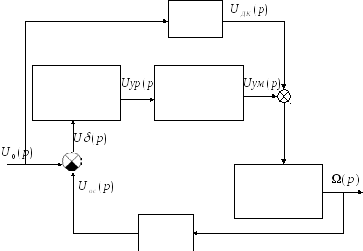
Рисунок 14 - Структурная схема в операторной форме.
Передаточная
функция разомкнутой цепи (без обратной
связи)
![]() равна произведению передаточных функций
контура регулирования:
равна произведению передаточных функций
контура регулирования:
![]()
![]()
![]()
Коэффициент усиления разомкнутого контура равен:
![]()
![]()
Передаточная функция замкнутой системы:
![]()
![]()
![]()
.
IV.Критерии устойчивости системы.
Запишем характеристическое уравнение замкнутой системы:
![]()
![]()
С![]() огласно
критерию Гурвица система 3его порядка
будет устойчивой, если произведение
коэффициентов средних членов больше
произведения крайних членов. Проверим
данное условие:
огласно
критерию Гурвица система 3его порядка
будет устойчивой, если произведение
коэффициентов средних членов больше
произведения крайних членов. Проверим
данное условие:
![]()
Условие выполняется, следовательно, система устойчивая.
Определим Kпр для системы третьего порядка:
![]()
![]()
![]()
![]()
Уменьшим найденное значение Кпр на 30% и примем эту величину равной коэффициенту передачи разомкнутого контура Кр:
![]()
По значению Кр вычислим необходимое значение коэффициента усиления усилителя рассогласования.
![]()
Отсюда
![]()
V. Исследование статической ошибки.
Определим значение статической ошибки для заданного входного воздействия и тип исследуемой системы регулирования.
Статическая ошибка
– это величина ошибки регулирования в
установившемся режиме, то есть значение
![]() при
при
![]()
Входное воздействие по условию 10 В. Тогда, зная передаточные функции звеньев, выразим сигнал ошибки через входное воздействие, преобразованное звеньями системы.
![]()
Входное воздействие в операторной области
![]()
Теперь выразим
![]() из структурной схемы (УР - УМ соединены
последовательно, УР-УМ с ДК соединены
параллельно, УР-УМ-ДК соединены
последовательно с ДВ-ДС):
из структурной схемы (УР - УМ соединены
последовательно, УР-УМ с ДК соединены
параллельно, УР-УМ-ДК соединены
последовательно с ДВ-ДС):
![]()
Подставим выражение
для
![]() в
выражение для
в
выражение для
![]() :
:
![]()
Перенесём слагаемые,
содержащие
![]() в левую часть:
в левую часть:
![]()
Приведем подобные
слагаемые, вынесем
![]() :
:
![]()
Получаем выражение
для
![]()
![]()
Подставляем значения постоянных времени и коэффициентов:
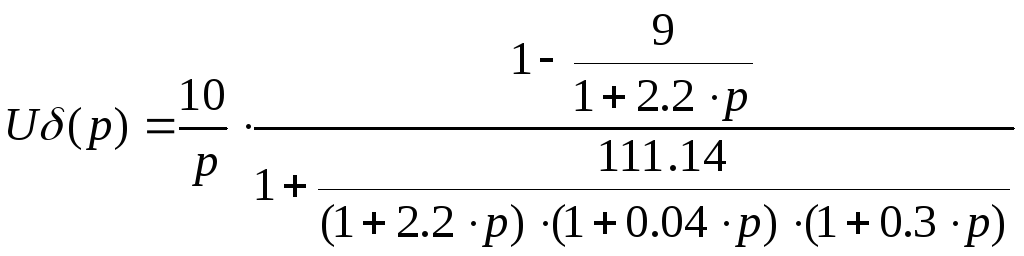
Упрощая полученное выражение, имеем:
![]()
Найдем по полученному изображению оригинал сигнала ошибки:
Режим статики –
установившийся режим:
![]() .
Воспользуемся предельной теоремой:
.
Воспользуемся предельной теоремой:
![]()
Значит:
![]() =
=
![]()
Ошибка регулирования не равна нулю, следовательно, система является статической.
VI.Частотные характеристики.
Передаточная функция разомкнутой системы:
![]()
Комплексный коэффициент передачи равен:
![]()
Найдем АЧХ:
![]()

Найдем ЛАЧХ:
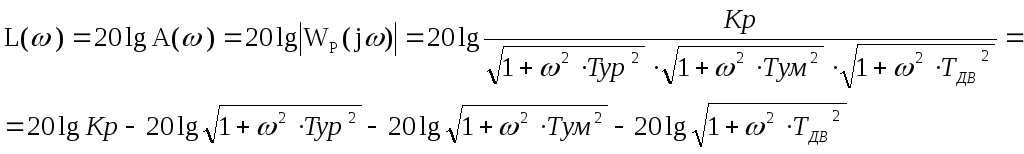
![]()
Найдем частоты сопряжения:
![]()
![]()
![]()
Получаем 4 интервала:
![]()
-
Если
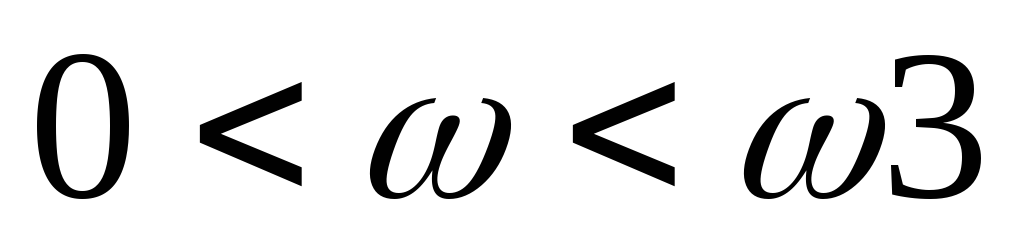 ,
то
,
то
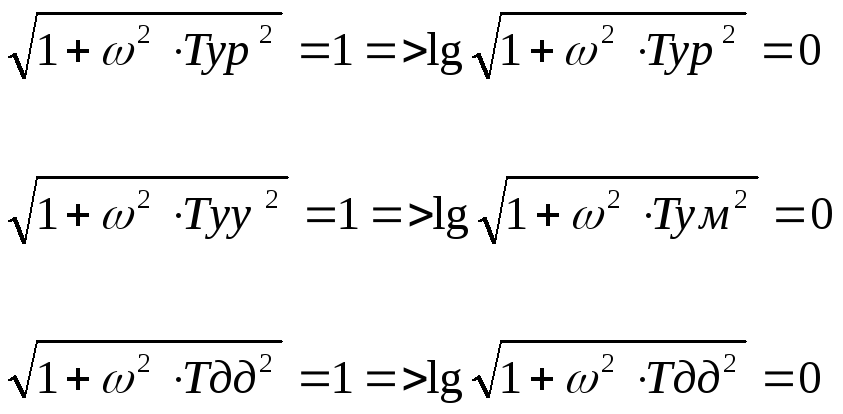
![]()
2. Если
![]() ,
то
,
то
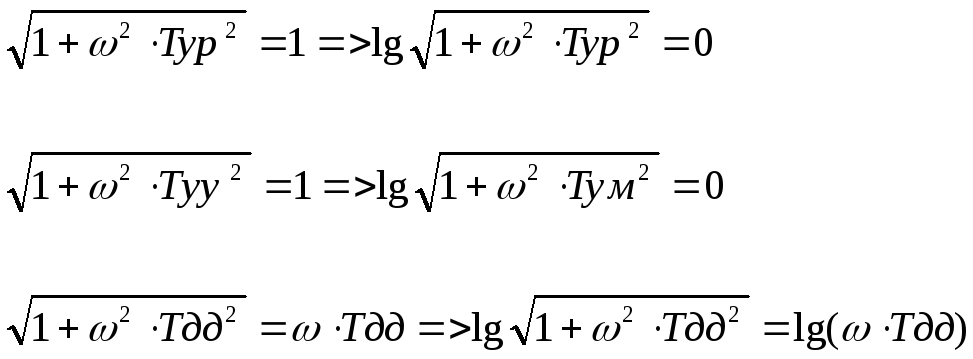
![]()
-
Если
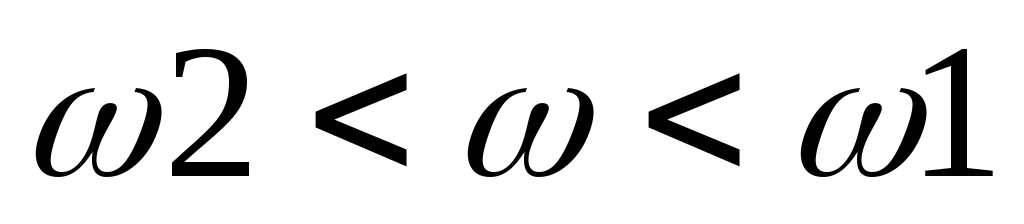 ,
то
,
то
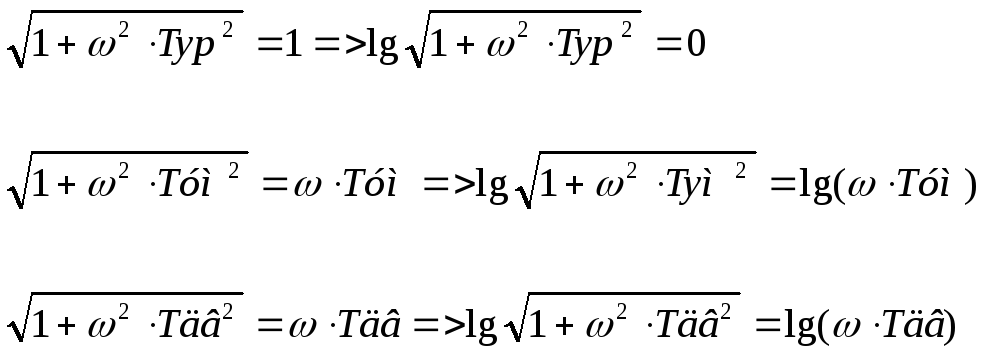
![]()
-
Если
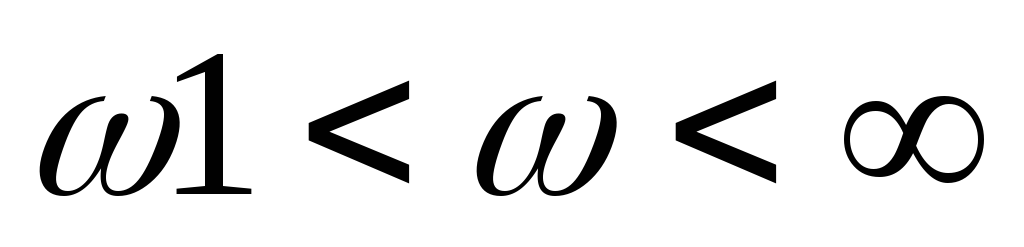 ,
то
,
то
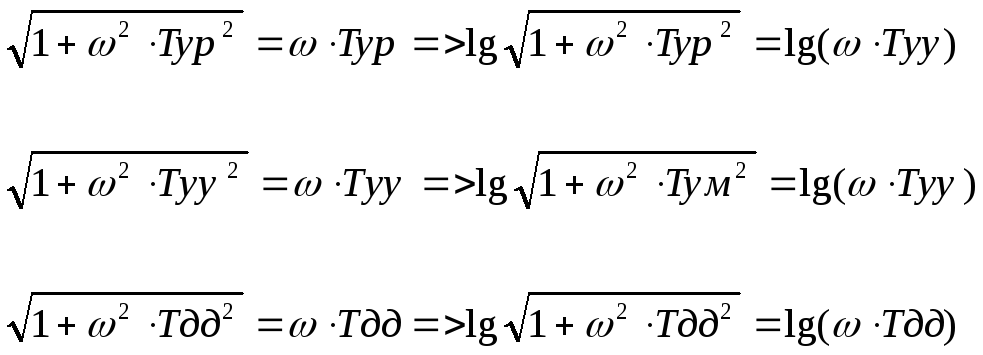
![]()
Найдем ФЧХ:
![]()
![]()
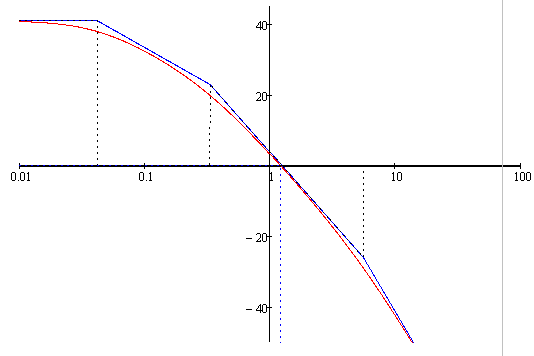
Рисунок 15 – График точной и асимптотической ЛАЧХ.
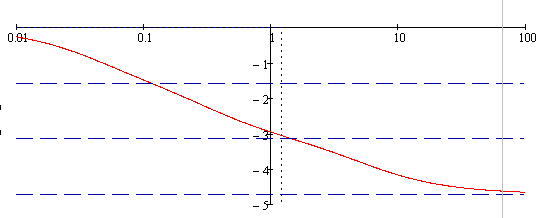
Рисунок 16 – График ЛФЧХ.
С помощью критерия
Найквиста определим устойчивость
системы. На частоте
![]() (когда ЛАЧХ равна нулю) ФЧХ больше –π,
поэтому система устойчива.
(когда ЛАЧХ равна нулю) ФЧХ больше –π,
поэтому система устойчива.
Чтобы найти
![]() поднимем график ЛАЧХ на 2.6 - так, чтобы
он пересекал ось частот на частоте, при
которой ФЧХ равна –π. (это частота 1.448)
Тогда система становится на границу
устойчивости и мы можем определить
значение
поднимем график ЛАЧХ на 2.6 - так, чтобы
он пересекал ось частот на частоте, при
которой ФЧХ равна –π. (это частота 1.448)
Тогда система становится на границу
устойчивости и мы можем определить
значение
![]() :
:
![]()
Рассчитанное в
пункте IV
значение
![]() - 160.2
- 160.2
Таким образом, значения практически совпадают.
