2.5. Важнейшие непрерывные случайные величины

1. Равномерная случайная величина.

Говорят, что непрерывная случайная величина имеет равномерный закон распределения (равномерное распределение) на отрезке , если множество ее возможных значений , а плотность вероятностей постоянна на этом отрезке:

Константа С при этом однозначно определяется из условия нормировки:

, то есть .

Таким образом, равномерно распределенная случайная величина имеет плотность вероятностей:

и для нее используется сокращенное обозначение: .

Найдем функцию распределения случайной величины .

Для этого рассмотрим три случая:

а) если , то ;

б) если ,то ;

в) если , то .

Окончательно имеем:

Графики плотности вероятностей и функции распределения случайной величины имеют вид:

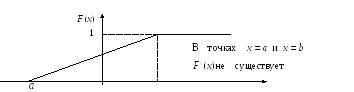
2. Показательная (экспоненциальная) случайная величина.

Говорят, что непрерывная случайная величина имеет показательный закон распределения (показательное, экспоненциальное распределение), если множество ее возможных значений , а плотность вероятностей имеет вид:

Число называется параметром показательного закона распределения, а для показательной случайной величины используется сокращенное обозначение: .

Проверим условие нормировки:

при любом .

Найдем функцию распределения случайной величины .

Для этого рассмотрим два случая:

а) если , то ;

в) если , то .

Окончательно имеем:

Графики плотности вероятностей и функции распределения случайной величины имеют вид:

3. Нормальная (гауссовская) случайная величина.

Говорят, что непрерывная случайная величина имеет нормальный закон распределения (нормальное, гауссовское распределение) с параметрами , если множество ее возможных значений , а плотность вероятностей имеет вид:

.

Сокращенное обозначение нормальной случайной величины:

.

Кривая плотности вероятностей имеет симметричный вид относительно прямой и имеет максимум в точке .

Проверим условие нормировки:

для любых значений параметров а и (при этом использовался известный в анализе факт, что - интеграл Пуассона).

В зависимости от изменения параметров плотность вероятностей нормального закона распределения меняется следующим образом.

Если параметр фиксирован, то при изменении а кривая , не изменяя своей формы, просто смещается вдоль оси абсцисс. Таким образом, параметр а является параметром сдвига (положения). Также параметр а характеризует среднее значение случайной величины.

Изменение при фиксированном а равносильно изменению масштаба кривой по обеим осям: при увеличении плотность вероятностей становится более плоской, растягиваясь вдоль оси абсцисс; при уменьшении - вытягивается вверх, одновременно сжимаясь с боков (эффект действия условия нормировки). Таким образом, параметр является параметром масштаба.

Также параметр характеризует степень разброса значений случайной величины около среднего значения а в следующем смысле. Чем меньше , тем больше при фиксированном вероятность вида , как площадь под плотностью вероятностей или, другими словами, тем при меньшем можно получить заданную вероятность вида . Это означает, что при уменьшении значения случайной величины более плотно группируются около а, то есть степень разброса значений случайной величины около среднего значения а меньше.

Если и , то нормальный закон распределения называется стандартным, его плотность вероятностей имеет вид:

и называется функцией Гаусса.

Функция распределения случайной величины имеет вид:

и не выражается в элементарных функциях. Функцию называют функцией Лапласа (или интегралом вероятностей).

Геометрическая иллюстрация.

Свойства функции Лапласа :

1. ;

2. для .

Значения функции Лапласа для табулированы.

Функция распределения случайной величины также выражается через функцию Лапласа :

.

Вероятность попадания случайной величины в заданный интервал определяется по формуле:

.

Наиболее просто выражается через функцию Лапласа вероятность попадания случайной величины в интервал длины , симметричный относительно точки :

.

Далее, если положить и учесть, что , то получаем:

.

Полученный результат носит название «Правило трех сигма». Он означает, что «практически все» значения случайной величины находятся внутри интервала в том смысле, что вероятность случайной величине принять значение, не принадлежащее этому интервалу, пренебрежимо мала ().

Геометрическая иллюстрация «Правила трех сигма».

Нормальный закон распределения очень распространен и имеет чрезвычайно большое значение для практики. В этом мы убедимся, когда познакомимся с центральной предельной теоремой.

5. Случайная величина, имеющая закон распределения Коши.

Говорят, что непрерывная случайная величина имеет закон распределения Коши, если множество ее возможных значений , а плотность вероятностей имеет вид:

.

Функция распределения случайной величины, распределенной по закону Коши, имеет вид:

.

Графики плотности вероятностей и функции распределения случайной величины, распределенной по закону Коши, выглядят следующим образом:

21