Решение задач является наиболее характерной
и специфической разновидностью свободного
мышления.
У. Джеймс
I. Пределы
1.1. Понятие о пределе числовой последовательности.
Последовательностью
называется
совокупность значений функции
натурального аргумента n.
Определение 1.1.
Число а
называется
пределом
числовой последовательности
,
если для любого
существует такое число N,
что
при
.
В этом случае
пишут:
.
Определение предела последовательности
можно записать с использованием
логических кванторов (
- квантор общности, читается «для любого»
или «для всех»;
- квантор существования, читается
«существует» или «найдется»):
,
если
Последовательность,
имеющая предел, называется сходящейся.
Для того, чтобы последовательность
имела предел, необходимо и достаточно,
чтобы она была монотонной и ограниченной.
Предел последовательности единственен,
если он существует. Если
,
то последовательность
называется бесконечно
малой.
Пример 1.1.
Рассмотрим последовательность
.
С ростом n
члены последовательности уменьшаются
и становятся сколь угодно мало
отличающимися от 0. Докажем, что
.
По определению
предела
,
если
.
Положим
.
Тогда
Это означает, что
.
Если
последовательности
-
бесконечно малые, а
-
ограниченная последовательность, то
последовательности
являются бесконечно малыми.
Пример 1.2.
,
т.к.
-
бесконечно малая, а
-
ограниченная последовательность. J
Если
,
то последовательность
называется бесконечно
большой.
Если последовательность бесконечно
большая, то она не ограничена.
Пример 1.3.
,
т.к.
члены
последовательности
с
ростом n
растут и становятся сколь угодно большими
при больших n.
J
1.2.Правила вычисления пределов последовательностей.
1.
;
2.
;
3.
;
4.
;
5.
при условии
.
J
Пример 1.4.
Найти пределы : 1)
;
2)
;
3)
.
Решение.
1) При
числитель и знаменатель стремятся к
бесконечности. Преобразуем данную
последовательность, разделив все члены
дроби на
.
Используя правила нахождения пределов,
найдём:
.
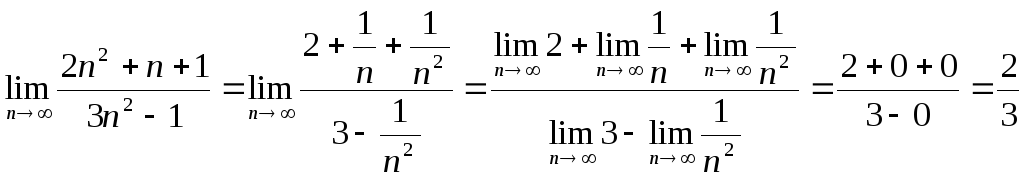2) Разделим все
члены дроби на
и используем необходимые правила:
.
3) Разделим все
члены дроби на
,
получим:
.
J
Воспользуемся
результатами приведённых примеров.
Если в условии задачи имеем неопределенность
вида
,
то:
1) если старшие степени n в числителе и знаменателе равны, то ответ равен отношению
коэффициентов при данных степенях
2) если
старшая степень n
находится в числителе, то ответ будет
;
3) если старшая степень находится в знаменателе, то ответ будет 0.
Если
,
то последовательности
и
называются эквивалентными, обозначение:
.
В решении примеров последовательности
можно заменять эквивалентными. Рассмотрим
решение примера 1.4 с использованием
эквивалентностей:
1)
;
2)
;
3)
.
Пример 1.5.
Найти
.
Решение.
Рассмотрим
числитель
.
Знаменатель эквивалентен 3n.
Таким образом,
.
J
Пример 1.6.
Найти
Решение.
Перейдем к
эквивалентным последовательностям и
найдем предел их отношения:
.
J
Пример 1.7.
Найти
Решение.
Имеем
неопределенность вида
.
Избавимся от иррациональности и
рассмотрим неопределенность
.
=
=
J
И от того, что что-то очень сложно, ты не
пытаешься это сделать? Научиться ходить
вначале тоже было тяжело, но ты позани-
мался, и теперь, глядя на тебя, может пока-
заться, что это все не трудно.
Р. Бах. Иллюзии
☼ Упражнения 1.1. Вычислить пределы:
1)
;
5)
;
9)
;
2)
;
6)
;
10)
;
3)
;
7)
; 11)
;
4)
;
8)
;
12)
.
☼