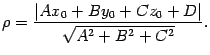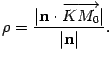Расстояние от точки до плоскости

Пусть плоскость  задана уравнением  и дана точка  . Тогда расстояние  от точки  до плоскости  определяется по формуле

(11.7)

        Доказательство.     Расстояние от точки  до плоскости  -- это, по определению, длина перпендикуляра  , опущенного из точки  на плоскость  (рис. 11.9).

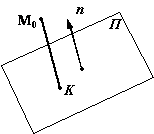
Рис.11.9.Расстояние от точки до плоскости

Вектор  и нормальный вектор n плоскости  параллельны, то есть угол  между ними равен 0 или  , если вектор n имеет направление противоположное, указанному на рис. 11.9. Поэтому

Откуда

(11.8)

Координаты точки  , которые нам неизвестны, обозначим  . Тогда  . Так как  , то  . Раскрыв скобки и перегруппировав слагаемые, получим

(11.9)

Точка  лежит на плоскости  , поэтому ее координаты удовлетворяют уравнению плоскости:  . Отсюда находим, что  . Подставив полученный результат в формулу (11.9), получим  . Так как  , то из формулы (11.8) следует формула (11.7).      

Билет 46. Декартовы прямоугольные координаты. Поворот осей на плоскости.

Мы рассматриваем преобразование, заключающееся в повороте координатных осей с сохранением начала координат (рис. 13).

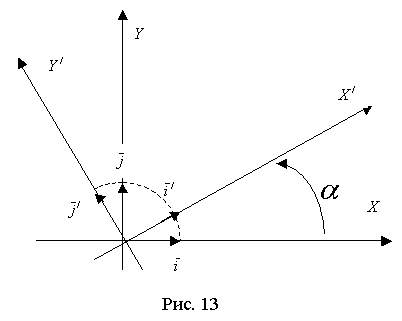
Пусть точка М имеет координаты (х, у) в "старой" системе и координаты (х,' у')в "новой" системе, α - угол поворота осей координат, отсчитываемый в положительном направлении от "старой" оси Ох. В данном случае происходит изменение базиса  на базис 

Запишем координаты векторов  и  в базисе 

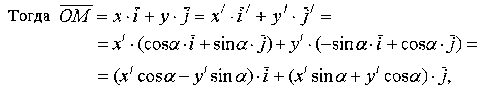
т.е., мы получили

или, в матричной форме

Формулы (43), (44) выражают "старые" координаты через "новые".

Обозначим матрицу

тогда

Как найти выражение "новых" координат через "старые"?

Поскольку матрица А невырожденная, то существует обратная матрица A^-1.

Умножим соотношение (45) слева на A^-1 и получим

поскольку A^-1*A, т.е. единичная матрица, то

где, очевидно,

Декартовы прямоугольные координаты на плоскости

Декартова прямоугольная система координат определяется заданием линейной единицы для измерения длин и двух взаимно перпендикулярных осей, занумерованных в каком-нибудь порядке.

Точка пересечения осей называется началом координат, а сами оси - координатными осями. Первая из координатных осей называется осью абсцисс, вторая - осью ординат.

Начало координат обозначается буквой О, ось абсцисс - символом Ох, ось ординат - символом Оу.

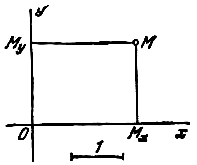
Координатами произвольной точки М в заданной системе называют числа

, 

( см. рис. 1), где  и  суть проекции точки М на оси Ох и Оу,  обозначает величину отрезка  оси абсцисс,  - величину отрезка  оси ординат. Число х называется абсциссой точки М, число у - ординатой этой же точки. Символ М(х; у) обозначает, что точка М имеет абсциссой число х, а ординатой число у.

Ось Оу разделяет всю плоскость на две полуплоскости; та из них, которая расположена в положительном направлении оси Ох, называется правой, другая - левой. Точно так же ось Оу разделяет плоскость на две полуплоскости; та из них, которая расположена в положительном направлении оси Оу, называется верхней, другая нижней.

Обе координатные оси вместе разделяют плоскость на четыре четверти, которые нумеруют по следующему правилу: первой координатной четвертью называется та, которая лежит одновременно в правой и в верхней полуплоскости, второй - лежащая в левой и в верхней полуплоскости, третьей - лежащая в левой и в нижней полуплоскости, четвертой - лежащая в правой и в нижней полуплоскости.

Билет 47. Виды уравнений прямой на плоскости: общее, в отрезках, параметрические и канонические. 

Общее уравнение прямой

Общее уравнение прямой линии на плоскости в декартовых координатах:

где A, B и C — произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A,B) называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.

При C = 0 прямая проходит через начало координат. Также уравнение можно переписать в виде :

Уравнение прямой в отрезках

Прямая линия, пересекающая ось Ox в точке  и ось Oy в точке :

В этом виде невозможно представить прямую, проходящую через начало координат.

Параметрические уравнения прямой

Параметрические уравнения прямой могут быть записаны в виде:

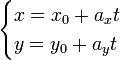
где t — производный параметр, a_x, a_y — координаты x и y направляющего вектора прямой, при этом

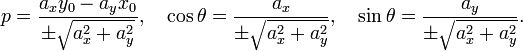
Параметр t пробегает все действительные значения.