Матрица поворота в двумерном пространстве

В двумерном пространстве поворот можно описать одним углом θ со следующей матрицей линейного преобразования в декартовой системе координат:

Положительным углам при этом соответствует вращение вектора против часовой стрелки в обычной, правосторонней системе координат, и по часовой в левосторонней системе координат.

Сам поворот происходит путём умножения матрицы поворота на вектор

Матрица поворота в трёхмерном пространстве

Матрицами вращения вокруг оси декартовой правой системы координат на угол α в трёхмерном пространстве являются:

• Вращение вокруг оси x:

,

• Вращение вокруг оси y:

,

• Вращение вокруг оси z:

,

В трёхмерном пространстве для описания поворота можно использовать

• три угла, например, углы Эйлера (γ,β,α),

• угол поворота θ и единичный вектор оси вращения ,

• матрицу поворота 3x3,

• кватернион.

Матрицы поворота вектора в декартовой системе координат, соответствующие первым двум способам задания поворота:

и

Однако, поскольку умножение матриц не коммутативно, то есть: , следовательно, положение системы координат после поворота вокруг трех осей будет зависеть от последовательности поворотов, то существует 6 различных видов матрицы поворота:

• 1) Поворот около осей: X -> Y -> Z

• 2) Соответственно: X -> Z -> Y

• 3) Y -> X -> Z

• 4) Y -> Z -> X

• 5) Z -> X -> Y

• 6) Z -> Y -> X

Получить же нужную матрицу можно путем последовательного перемножения матриц поворота около одной оси (приведенных выше) в соответствии с желаемым порядком.

Билет 33. Свойства обратной матрицы

33) Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

1), где обозначает определитель.

2)для любых двух обратимых матриц A и B.

3)где * ^T обозначает транспонированную матрицу.

4)для любого коэффициента .

5)Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A ^{− 1} существует, то x = A ^{− 1}b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.

Матричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.

Пусть дана система линейных уравнений с n неизвестными (над произвольным полем):

Тогда её можно переписать в матричной форме:

AX = B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:

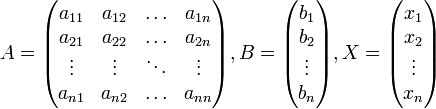
Умножим это матричное уравнение слева на A ^{− 1} — матрицу, обратную к матрице A:

Так как A ^{− 1}A = E, получаем X = A ^{− 1}B. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:

.

Для однородной системы линейных уравнений, то есть когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (то есть ненулевое) решение только если det A = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.

Билет 34. Теорема о связи решений однородной и неоднородной СЛАУ.

Неоднородная система: Ax=B, B≠0.

Однородная система: Ах=0.

Теорема: 1. Если вычесть два решения неоднородной системы, то получится решение однородной системы.

2. Если к решению неоднородной системы прибавить решение однородной системы, то получится решение неоднородной системы.

Доказательство:

1) с¹,с² – два решения неоднородной системы.

Ас¹=В; Ас²=В. Из первой системы вычтем вторую систему: Ас¹-Ас²=0; А(с¹-с²)=0; с¹-с² – решение однородной системы.

2) Ас^н=В – решение неоднородной системы.

Ас^о=0 - решение однородной системы.

Ас^н+ Ас^о=В. А(с^н+ с^о)=В. с^н+ с^о – решение неоднородной системы.

Билет 35. Несовместность СЛАУ. Метод Гауса.

Если система решений не имеет, то она называется несовместной.

Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа:

1)На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.

2)На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.

Билет 36. Прямая с угловым коэффециентом. Угол между 2-мя прямыми. Пучок прямых.

Уравнение y=kx+b называется уравнением прямой с угловым коэффициентом; k - угловой коэффициент, b - величина отрезка, который отсекает прямая на оси Оу, считая от начала координат. Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой. k=tg(альфа).

Угол между двумя прямыми:

Первая прямая: L₁, n₁(p₁,q₁,r₁).

Вторая прямая: L₀, n₀(p,q,r).

L₁// L₀; n₁// n₀; p₁/р=q₁/q= r₁/r – условие параллельности 2 прямых.

L₁﬩ L₀; n₁﬩n₀; (n₁,n)=0; pp₁+qq₁+rr₁=0 – условие параллельности 2 прямых.

Cosφ=(n₁,n)/|n₁|*|n₀|

В плоскости Лобачевского две прямые могут либо пересекаться, либо могут быть параллельными в некотором направлении, либо расходящимися. Поэтому в плоскости Лобачевского существует три вида пучков прямых:

1) пучок прямых, пересекающихся в одной точке, называемой центром пучка; такой пучок называется центральным или эллиптическим;

2) пучок прямых, параллельных в заданном направлении некоторой прямой, называемой осью пучка; такой пучок называется параболическим;

3) пучок расходящихся прямых, перпендикулярных к некоторой прямой, называемой базой пучка; такой пучок называется гиперболическим.

Билет 37. Взаимное расположение прямых на плоскости. Расстояние от точки до прямой.

Взаимное расположение прямых на плоскости.

Прямые  линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися. Рассмотрим подробнее каждый случай.

1. Параллельные прямые линии.

Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек.

Проекции параллельных прямых на любую плоскость (не перпендикулярную данным прямым) - параллельны. Если AB//CD то A₁B₁//C₁D₁; A₂B₂//C₂D₂; A₃B₃//C₃D₃(рис.33). В общем случае справедливо и обратное утверждение.