Пример выполнения контрольной работы

Задача 1. Горизонтальная балка АВ длиной 12 м шарнирно укреплена правым концом в неподвижной точке В, а левым концом А опирается катками на гладкую горизонтальную плоскость. К балке в точке D под углом 30^о к горизонту приложена сила F=8 кН. На правую половину балки действует нагрузка, распределенная треугольником, причем наибольшая ее интенсивность q_o=2 кН/м. К балке приложена также пара сил с моментом М=32 кНм. Определить реакции в опорах А и В, весом балки пренебречь (рис. 1).

Решение. Рассмотрим равновесие балки АВ. В числе активных сил на балку действует нагрузка, распределенная треугольником, Заменим эту нагрузку одной сосредоточенной силой – равнодействующей . Модуль равен площади треугольника. Высота его равна наибольшей интенсивности q_o, а основанием служит часть балки ВK=6 м. Итак,

кН. (1)

Равнодействующая приложена в центре тяжести С треугольника, т.е. в точке пересечения медиан. Из геометрии известно, что ВС:СК=2:1. Заметив, что ВС/СК=ВЕ/ЕК, найдем ВЕ=2ЕК=2·2=4 м.

Рис. 1

К балке приложены активные силы и моменты: сила , сила и пара сил с моментом М. На балку действует две связи – опоры А и В. Заменим связи реакциями связей ,и. Итак, балка находится в равновесии под действием активных сил и , активной пары сил с моментом М, а также реакций ,и. Задача статически определенная при трех неизвестных можно составить три уравнения равновесия. Составим уравнения равновесия

, (2)

, (3)

. (4)

Из уравнения (2) находим

кН. (5)

Из уравнения (4) при АВ=12 м, BL=DB·sin 30^o=5 м, ВЕ=4 м находим

. (6)

Из уравнения (3) находим

кН.

Задача 2. Компрессор, имея угловую скорость вращения п= 90 об/мин остано­вился совершив 12 оборотов. Определить время вращения компрессора t, скорость и ускорение а в точке компрессора на радиусе R= 0,8 м, показать их на схеме.

Решение.

.

Рис. 2

Задача 3. Автомобиль с прицепом общим весом =40 кН движется по подъему =0,002 (рис. 3). Сопротивление его движению составляет =0,3 Н на 1 кН веса. На протяжении = 750 м скорость автомобиля изменяется от =18 до =36 км/ч. Определить силу тяги автомобиля.

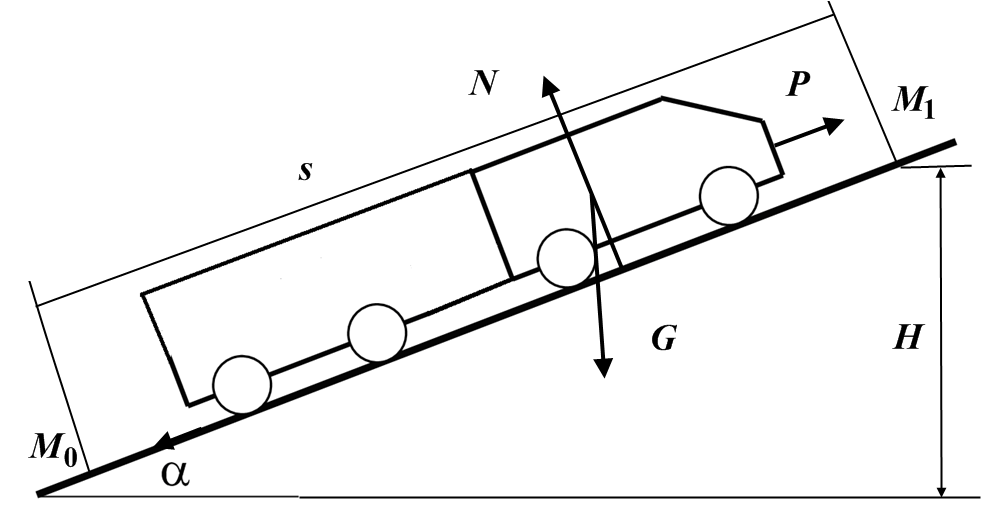
Рис. 3

Решение. Движение автомобиля – поступательное. Применим теорему об изменении кинетической энергии на перемещении М_оМ₁. Скорость автомобиля в точке М_о равна v_o=18 км/ч=5 м/с, в точке М₁ равна v₁=36 км/ч=10 м/с. На автомобиль действуют силы постоянные - сила тяги, - вес поезда, - нормальная реакция, - сила сопротивления движению (F=0,003G). Составим уравнение изменения кинетической энергии:

,

где

.

Вычислим работы сил:

,

.

Тогда

,

Откуда

.