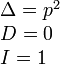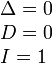- •1 Векторы
- •Свойства
- •Линейные операции над векторами ]Сложение векторов ]Сложение геометрических векторов
- •]Сложение коллинеарных скользящих векторов
- •Сложение векторов - элементов линейного пространства
- •Умножение вектора на число
- •Скалярное произведение
- •Векторное произведение
- •Смешанное произведение
- •2 Прямая Уравнения прямой на плоскости
- •Общее уравнение прямой
- •Уравнение прямой в полярных координатах
- •Тангенциальное уравнение прямой
- •Уравнения прямой в пространстве
- •Взаимное расположение нескольких прямых на плоскости
- •Некоторые характеристические свойства плоскости
- •Уравнения плоскости
- •Связанные понятия
- •Классификация кривых второго порядка Невырожденные кривые
- •Вырожденные кривые
- •Канонический вид
- •Определение через разложение по первой строке
- •Свойства определителей
- •Операции над матрицами
- •Метод Гаусса—Жордана
- •Методы решения (нажать с ctrl)
- •Непрерывная функция
Канонический вид
Вводом
новой системы координат можно привести
уравнения кривых второго порядка к
стандартному каноническому виду (см.
таблицу). Параметры канонических
уравнений весьма просто выражаются
через инварианты ![]() и
корни характеристического уравнения
и
корни характеристического уравнения ![]() (см.
выше раздел «Характеристическая
квадратичная форма и характеристическое
уравнение»).
(см.
выше раздел «Характеристическая
квадратичная форма и характеристическое
уравнение»).
|
Вид кривой |
Каноническое уравнение |
Инварианты |
|
Невырожденные
кривые ( |
||
|
Эллипс |
|
|
|
Гипербола |
|
|
|
Парабола |
|
|
|
Вырожденные кривые (Δ = 0) |
||
|
Точка |
|
|
|
Две пересекающиеся прямые |
|
|
|
Две параллельные прямые |
|
|
|
Одна прямая |
x2 = 0 |
|
Для
центральной кривой в каноническом виде
её центр ![]() находится
в начале координат.
находится
в начале координат.
6 Операторы
Определитель
Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равны). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.
Определитель матрицы А обозначается как: det(A), |А| или Δ(A).
Определение через разложение по первой строке
Схема
расчета определителя матрицы ![]() .
.
Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:
![]()
Для
матрицы ![]() детерминант
определяется как
детерминант
определяется как

Для
матрицы ![]() определитель
задаётся рекурсивно:
определитель
задаётся рекурсивно:
 ,
где
,
где ![]() — дополнительный
минор к
элементу a1j.
Эта формула называется разложением
по строке.
— дополнительный
минор к
элементу a1j.
Эта формула называется разложением
по строке.
В
частности, формула вычисления определителя
матрицы ![]() такова:
такова:

= a11a22a33 − a11a23a32 − a12a21a33 + a12a23a31 + a13a21a32 − a13a22a31
Свойства определителей
-
Определитель — кососимметричная полилинейная функция строк (столбцов) матрицы. Полилинейность означает, что определитель линеен по всем строкам (столбцам):
 ,
где
,
где  и т. д. —
строчки матрицы,
и т. д. —
строчки матрицы,  —
определитель такой матрицы.
—
определитель такой матрицы. -
При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.
-
Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.
-
Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.
-
Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).
-
Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
-
Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.
-
Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.
-
Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
-
Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей (cм. также формулу Бине-Коши).
-
С использованием индексной нотации определитель матрицы 3×3 может быть определён с помощью символа Леви-Чивита из соотношения:
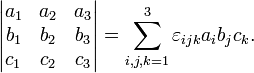
Матрица
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы