Векторное произведение

Основная статья: Векторное произведение

Векторным произведением вектора a на вектор b называется вектор c, удовлетворяющий следующим требованиям:

• длина вектора c равна произведению длин векторов a и b на синус угла φ между ними

• вектор c ортогонален каждому из векторов a и b

• вектор c направлен так, что тройка векторов abc является правой.

Обозначение: 

Геометрически векторное произведение  есть ориентированная площадь параллелограмма, построенного на векторах , представленная псевдовектором, ортогональным этому параллелограмму.

Свойства векторного произведения:

1. При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е 

2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть 

3. Векторное произведение обладает распределительным свойством: 

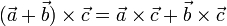
Смешанное произведение

Основная статья: Смешанное произведение

Сме́шанное произведе́ние  векторов  — скалярное произведение вектора  на векторное произведение векторов  и :

(равенство записано для разных обозначений скалярного и векторного произведения).

Иногда смешанное произведение называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее —псевдоскаляр).

Геометрически смешанное произведение  есть (ориентированный) объём параллелепипеда, построенного на векторах .

2 Прямая Уравнения прямой на плоскости

Способы задания прямой:  или .

Общее уравнение прямой

Общее уравнение прямой линии на плоскости в декартовых координатах:

где A, B и C — произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A,B) называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.

При C = 0 прямая проходит через начало координат. Также уравнение можно переписать в виде :

Уравнение прямой с угловым коэффициентом

Уравнение прямой с угловым коэффициентом. Прямая линия, пересекающая ось Oy в точке  и образующая угол  с положительным направлением оси Ox:

Коэффициент k называется угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси Oy.

Уравнение прямой в отрезках

Прямая линия, пересекающая ось Ox в точке  и ось Oy в точке :

В этом виде невозможно представить прямую, проходящую через начало координат.

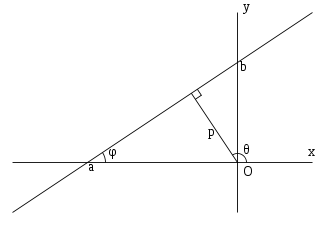
Нормальное уравнение прямой

где p — длина перпендикуляра, опущенного на прямую из начала координат, а θ — угол (измеренный в положительном направлении) между положительным направлением оси Ox и направлением этого перпендикуляра. Если p = 0, то прямая проходит через начало координат, а угол  задаёт угол наклона прямой.

Уравнение прямой, проходящей через две заданные несовпадающие точки

Уравнение прямой, проходящей через две заданные несовпадающие точки  и 

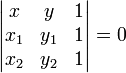
или

или в общем виде

Векторно-параметрическое уравнение прямой

Векторно-параметрическое уравнение прямой задается вектором  конец которого лежит на прямой, и направляющим вектором прямой . Параметр t пробегает все действительные значения.

Параметрические уравнения прямой

Параметрические уравнения прямой могут быть записаны в виде:

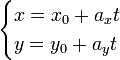
где t — производный параметр, a_x, a_y — координаты x и y направляющего вектора прямой, при этом

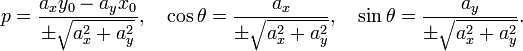
Смысл параметра t аналогичен параметру в векторно-параметрическом уравнении.

Каноническое уравнение получается из параметрическиx уравнений делением одного уравнения на другое:

где  — координаты  и  направляющего вектора прямой,  и  координаты точки, принадлежащей прямой.