
- •Варфоломеева а.С., Кургузов н.Н., Кургузова л.И., Леньков ю.А., Никитин к.И.
- •Учебное пособие. Омск: Изд-во ОмГту, 2007. 197 с.
- •Содержание
- •Введение
- •1 Нагревание проводников и электрических аппаратов
- •1.1 Допустимые максимальные температуры электрических аппаратов и проводников в нормальном режиме и при коротком замыкании
- •1.1.1Общие сведения
- •1.1.2 Изолированные проводники электрического тока в нормальном режиме
- •1.1.3 Неизолированные токоведущие части аппаратов в нормальном режиме
- •1.1.4 Изолированные и неизолированные токоведущие части аппаратов при коротких замыканиях
- •1.1.5 Нетоковедущие части аппаратов
- •1.2 Нагрев проводников и аппаратов
- •1.2.1 Общие сведения
- •1.2.2 Активные потери энергии в проводниках и электрических аппаратах
- •1.2.2.1 Потери в токоведущих частях
- •1.2.2.2 Потери в нетоковедущих ферромагнитных деталях аппаратов
- •1.2.2.3 Потери в диэлектриках
- •1.3 Способы передачи тепла внутри нагретых тел и с их поверхности
- •1.4 Установившийся режим нагрева проводников и аппаратов
- •1.4.1 Общие сведения
- •1.4.2 Тепловой расчёт неизолированных проводников в установившемся режиме
- •1.4.3 Тепловой расчёт изолированных проводников и кабелей
- •1.4.4 Нагревание аппаратов в установившимся режиме
- •1.4.5 Выбор проводников и аппаратов по условиям продолжительного режима
- •1.5 Нагрев проводников и аппаратов в переходных режимах
- •1.6 Примеры теплового расчета
- •Задание №1
- •2 Термическая и электродинамическая стойкость электрических проводников и аппаратов
- •2.1 Нагрев проводников и аппаратов при коротком замыкании
- •2.2 Термическая стойкость проводников и аппаратов
- •2.2.1 Термическая стойкость неизолированных проводников
- •2.2.2 Термическая стойкость кабелей
- •2.2.3 Термическая стойкость электрических аппаратов
- •2.3 Определение импульса квадратичного тока короткого замыкания
- •2.4 Электродинамические усилия в электрических проводниках и аппаратах
- •2.4.1 Общие сведения
- •2.4.2 Методы расчёта электродинамических усилий
- •2.4.3 Усилия между параллельными проводниками
- •2.4.4 Усилия и моменты, действующие на взаимно перпендикулярные проводники
- •2.5 Электродинамические силы в трёхфазной шинной линии при различных видах короткого замыкания
- •2.5.1 Общие сведения
- •2.5.2 Электродинамические силы в трёхфазной шинной линии при трёхфазном коротком замыкании
- •2.5.3 Электродинамические силы в трёхфазной шинной линии при двухфазном коротком замыкании
- •2.6 Электродинамическая стойкость проводников и электрических аппаратов
- •2.6.1 Электродинамическая стойкость проводников
- •2.6.2 Электродинамическая стойкость аппаратов
- •2.7 Примеры расчета термической и электродинамической стойкости проводников и аппаратов
- •Задание №2
- •3 Электрические контакты
- •3.1 Назначения и требования к электрическим контактам
- •3.2 Сопротивление электрического контакта
- •3.3 Нагрев контактных соединений
- •3.3.1 Нагрев контактных соединений при номинальном токе
- •3.3.2 Нагрев контактных соединений при токах короткого замыкания
- •3.4 Конструкция контактных соединений и контактов
- •3.5 Пример расчета нагрева контактных соединений
- •Задание №3.
- •4 Отключение цепей постоянного и переменного тока
- •4.1 Общие сведения
- •4.2 Электрическая дуга
- •4.3 Возбуждение атома.
- •4.4 Ионизация
- •4.4.1 Термоэлектронная эмиссия.
- •4.4.2 Автоэлектронная (электростатическая) эмиссия.
- •4.4.3 Ионизация столкновением
- •4.5 Ударная ионизация
- •4.6 Термическая диссоциация и ионизация.
- •4.7 Деионизация дугового промежутка осуществляется путем рекомбинации и диффузии.
- •4.7.1 Рекомбинация (воссоединение)
- •4.8 Диффузия
- •4.9. Подвижностью ионов (электронов)
- •4.10 Радиационный захват электрона
- •4.11 Классификация дуг
- •4.11.1 Область катодного падения напряжения
- •4.11.2 Область анодного падения напряжения.
- •4.11.3 Ствол дуги
- •4.11.4 Турбулентная конвекция.
- •4.11.5 Баланс энергии в стволе дуги.
- •4.12 Потоки плазмы в дуге
- •4.13 Воздействие внешнего магнитного поля
- •4.14 Дуга постоянного тока и ее характеристики
- •4.15 0Тключение электрических цепей постоянного тока
- •4.15.1 Условия стабильного горения и гашения дуги
- •4.15.2 Открытый разрыв
- •4.15.3 Дугогасительные устройства с узкой щелью
- •4.15.4 Дугогасительные решетки
- •4.15.5 Гашение дуги под воздействием магнитного поля
- •4.16 Электрическая дуга переменного тока и ее характеристики
- •4.17 Отключение электрических цепей переменного тока
- •4.17.1 Отключение активной цепи переменного тока
- •4.17.2.Отключение индуктивной цепи переменного тока
- •4.18 Гашение электрической дуги в выключателях переменного тока
- •4.18.1 Гашение электрической дуги в потоке сжатого воздуха
- •4.18.2 Гашение электрической дуги в элегазе
- •4.18.3 Гашение электрической дуги в трансформаторном масле
- •4.18.4 Гашение электрической дуги в вакууме
- •4.18.5 Гашение электрической дуги с помощью электромагнитного поля
- •4.19 Примеры расчета отключения цепей постоянного и переменного тока
- •Задание №4
- •5 Восстанавливающееся напряжение на контактах выключателя
- •5.1 Параметры восстанавливающегося напряжения
- •5.2 Расчет параметров восстанавливающегося напряжения в однофазной системе
- •5.3 Расчет параметров восстанавливающегося напряжения в трехфазных эффективно-заземленных сетях
- •5.4 Вторая стадия переходного процесса
- •5.5 Номинальные характеристики пвн
- •5.6 Пример расчета параметров пвн на полюсах выключателя
- •6 Электромагниты
- •6.1Электромагниты постоянного тока
- •6.2 Поляризованные электромагниты и постоянные магниты
- •6.3 Электромагниты переменного тока
- •6.4 Примеры расчета электромагнитов
- •1‑Основание; 2‑сердечник; 3‑полюсный наконечник; 4‑якорь
- •Задание №5
- •1 ‑ Якорь; 2 ‑ фланец верхний; 3 ‑ корпус; 4 ‑ фланец нижний; 5 ‑ стоп; 6 ‑ латунная втулка
- •1 ‑ Фланец верхний; 2 ‑ якорь; 3 ‑ стоп; 4 ‑ корпус; 5 ‑ фланец нижний
- •1 ‑ Фланец верхний; 2 ‑ якорь; 3 ‑ стоп; 4 ‑ корпус; 5 ‑ фланец нижний
- •1 ‑ Основание; 2 ‑ сердечник; 3 ‑ полюсный наконечник; 4 ‑ якорь
- •1 ‑ Якорь; 2 ‑ основание; 3 ‑ сердечник; 4 – катушка
- •1 ‑ Якорь; 2 ‑ верхняя плита; 3 ‑ нижняя плита; 4 – полюс.
- •Литература
- •Приложение
6.3 Электромагниты переменного тока
При подаче синусоидального напряжения на обмотку однофазного электромагнита в ненасыщенном состоянии в нем возникает поток Ф = Фmsinωt, где Фm = U/4.44fω, ω=πf.
Мгновенное значение силы одного полюса электромагнита равно
![]() .
(6.20)
.
(6.20)
Сделав преобразования, получим
![]() (6.21)
(6.21)
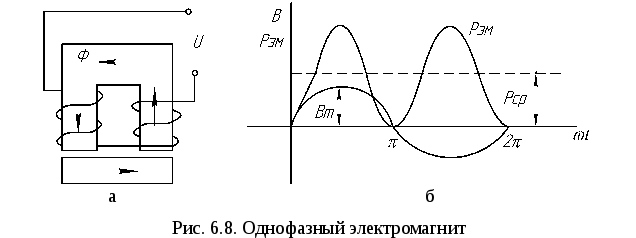
Результирующие значение мгновенной силы в однофазном электромагните с переменным магнитным потоком изменяется от нуля до своего максимального значения Рm = Фm2/(6μ0S) с двойной частотой (рис. 6.8).
Первый член в уравнении (6.21) представляет собой среднее значение силы за период, принимаемое за расчетное значение полезной силы. Если ее выразить через действующее значение магнитного потока Ф, получим формулу
![]() ,
(6.22)
,
(6.22)
совпадающую по форме с уравнением силы в электромагните постоянного тока. В отличие от последнего тяговая сила Рср = f(δ) у электромагнита переменного тока с обмоткой параллельного включения будет возрастать по ходу якоря незначительно.
Среднее значение силы на рис. 6.8.б показано пунктирной линией проходит посередине между нулем и максимальным значением мгновенной силы.
Второй член в (6.21) представляет переменную составляющую силы. Которая приводит к вредным явлениям вибрации якоря в электромагните. На практике переменная составляющая по возможности подавляется снижается до определенного значения применением специальных мер. Таким образом, сила, действующая на один полюс электромагнита, будет Рэм =Рср(1- соs2ωt).
Так как однофазный электромагнит имеет два полюса одинакового сечения, через которые проходит один и тот же магнитный поток, мгновенная сила, действующая на якорь, равна Ррез = 2Рэм = 2Рср(1- соs2ωt). Предположим что два электромагнита, подобных изображенному на рис. 6.8 а, имеют общий якорь, а обмотки их подключены к источникам, напряжения которых имеют одинаковые амплитуды, но сдвинуты по фазе на угол α (рис 6.9). В этом случае получаем двухфазный электромагнит. По каждой из двух частей магнитопровода проходят переменные синусоидальные магнитные потоки Ф1 = Фmsinωt; Ф2 = Фmsin(ωt+α). Тогда значение силы в каждой части будет соответственно Р1 = 2Рср(1-cos2ωt), Р2 = 2Рср[1-cos2(ωt+α)] где Рср - среднее значение силы, действующей в одном зазоре.
а
б
Рис 6.9 Двухфазных
электромагнит
Результирующая сила, приложенная к якорю, равна
Ррез=Р1+Р2, (6.23)
или
![]() .
(6.24)
.
(6.24)
Как видно, эта сила также изменяется во времени, однако никогда не доходит до нуля. Минимальное значение силы будет равно
![]() ,
(6.25)
,
(6.25)
а максимальное значение
![]() .
(6.26)
.
(6.26)
Значение максимальной и минимальной силы зависит от угла сдвига фаз α между потоками. Если α достигает 90°, суммарная сила становится постоянной (рис. 6.9,б).
В электромагните, показанном на рис. 6.9,а, По центральному сердечнику будет проходить магнитный поток, равный векторной сумме магнитных потоков каждой фазы. В таких электромагнитах кроме пульсации значения результирующей силы будет перемещаться и точка ее приложения. Даже при α=90°, когда результирующая сила будет постоянной, точка ее приложения будет перемещаться с удвоенной частотой в пределах от а до б (рис. 6.9,а). Перемещение точки приложения силы вызывает дребезжание якоря.
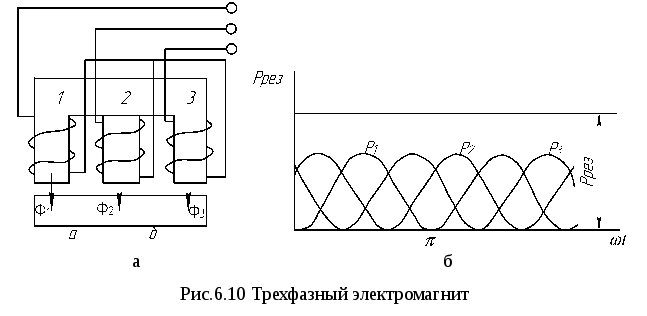
На рис. 6.10,а показан электромагнит с трехфазной магнитной системой, на каждом сердечнике которой по одной обмотке, питающейся от своей фазы источника трехфазного тока. Магнитные потоки в сердечниках сдвинуты по отношению друг к друг на 120°. Диаграмма действующих электромагнитных сил в трехфазном электромагните показана на рис. 6.10,б. Для этой системы Ф1 = Фmsinωt ; Ф2 = Фmsin(ωt+120°); Ф3 = Фmsin(ωt+240°). Результирующая сила Ррез=Р1+Р2 +Р3,
![]() (6.27)
(6.27)
Как видно, результирующее значение силы остается неизменным во времени. Точка ее приложения с двойной частотой перемещается между точками а и b, лежащими на серединах расстояний между осями смежных полюсов.
В настоящее время наиболее широкое распространение получили однофазные электромагниты с расщепленными экранированными полюсами. В магнитном отношении они аналогичны двухфазным электромагнитам. Однако второй, сдвинутый по фазе магнитный поток в них получается не с помощью обмотки, питаемой от внешнего источника, а с помощью специального экрана (короткозамкнутого витка) охватывающего часть магнитопровода.
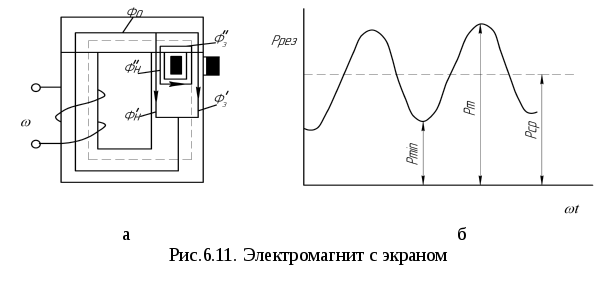
Магнитный поток Ф0, создаваемый намагничивающей обмоткой, разветвляется на две части Ф/н и Ф/э, замыкающиеся через две части сердечника: участок, не охваченный обмоткой, и участок, на котором расположен экранирующий виток. Благодаря протекающему по экранирующей обмотке току, который возникает за счет наводимой в ней противо - ЭДС, создается дополнительный поток Ф//н= Ф//э. На экранированном участке сердечника потоки вычитаются (векторно), а на неэкранированном - складываются. Так как этот дополнительный поток отстает по фазе от потоков Ф/н и Ф/э, в полюсах получаются разные по фазе потоки и результирующая сила, действующая на якорь включенного в сеть электромагнита, не должна быть ниже определенной минимальной величины Рmin (рис 6.11,б), благодаря чему уменьшается амплитуда пульсации силы.
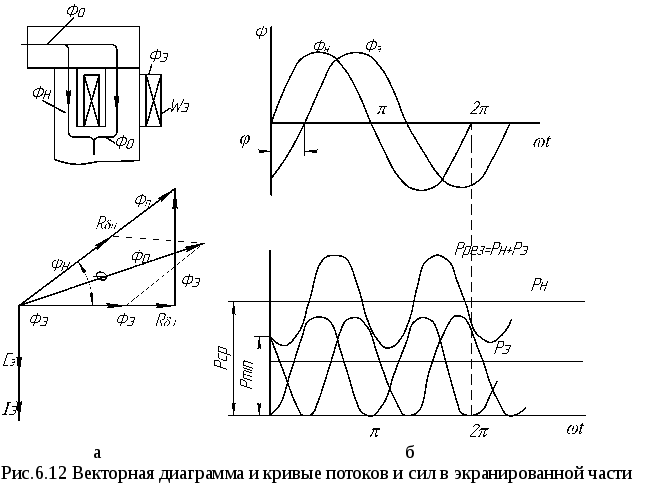
На рис. 6.12,а показан эскиз расщепленного полюса, правая часть которого охвачена короткозамкнутым экранирующим витком (или обмоткой ωэ). Общий магнитный поток Ф0 определяется как геометрическая сумма потоков Фн и Фэ. Магнитный поток в экранированной части Фэ от общего магнитного потока Ф0 на угол φэ, а поток в неэкранированной части Фн опережает поток на угол φн. Сдвиг фаз между потоками экранированной и неэкранированной частей φ=φэ+φн (рис. 6.12,б). Величина угла сдвига фаз между потоками определяется уравнением
![]() ,
(6.28)
,
(6.28)
где Хмэ ‑ реактивное магнитное сопротивление экрана; Rδэ ‑ магнитное сопротивление воздушного рабочего зазора над экранированной частью полюса.
На рис.6.12 показаны кривые изменения потоков Фн и Фэ, а на рис. 6.12,г- кривые соответствующих им сил Рн и Рэ, а так же результирующей силы Ррез=Рн+Рэ в функции ωt. Как показано на том же рисунке, необходимо, чтобы Рmin было больше противодействующей силы Рп. Коэффициент запаса по силе kр=Рmin/Pн должен быть больше единицы (обычно 1,1-1,2). Для уменьшения потерь на вихревые токи и перемагничивание магнитные системы электромагнитов переменного тока выполняют из тонколистовой стали с высоким удельным электрическим сопротивлением. При включении обмотки электромагнита под напряжение его динамические процессы описываются, как и для электромагнита постоянного тока, системой уравнений, одно из которых характеризует электромагнитные процессы, а второе — механические. Для электромагнита с поступательным перемещением якоря х имеем
![]() ,
(6.29а)
,
(6.29а)
![]() .
(6.29б)
.
(6.29б)
Здесь Um — амплитудное значение напряжении питания; ω — угловая частота; α— начальная фаза напряжения.
Рассмотрим период трогания и период движения электромагнита при срабатывании. Считая, что в периоде трогания магнитная цепь ненасыщенна, пренебрегая вихревыми токами, гистерезисом и влиянием короткозамкнутых витков (для времени трогания δ = δн), получаем из (6.29а)
![]() .
(6.30)
.
(6.30)
Решая (6.30) относительно тока, получаем
![]() (6.31)
(6.31)
где Zн ‑ полное сопротивление обмотки при начальном положении якоря; φ ‑ угол сдвига между током и напряжением; τн ‑ постоянная времени обмотки.
Постоянную времени обмотки τн можно выразить через добротность Qн:
![]() (6.32)
(6.32)
Обозначив γ=α-φ и ki=i/Im, где Im=Um/Zm сможем представить (6.32) в относительных единицах:
![]() (6.33)
(6.33)
Оно характеризует переходный процесс при включении электромагнита в период трогания. Как видно из (6.33), кривая тока содержит периодическую и апериодическую составляющие, а характер ее зависит от параметра γ (т. е. от начальной фазы напряжения α и сдвига по фазе между током и напряжением φ), а также от добротности обмотки.
Считая, что якорь реагирует на мгновенное значение электромагнитной силы, временем трогания будем считать то время, в течение которого ток нарастает от нуля до тока трогания Iтр.
Электромагнитное усилие пропорционально квадрату тока, поэтому время трогания можно найти из зависимости
![]() ,
(6.34)
,
(6.34)
где kiтр=Iтр/Im.
Минимальное время трогания (6.19), считая‚ γ = 0 равно
![]() .
(6.35)
.
(6.35)
Как видно из (6.35), минимальное время меняется в пределах от 0 (при Iтр=0) до четверти периода напряжения питания 1/(4f) (при Iтр=Im, Uтр=Um). Если kiтр>1, (6.35) теряет смысл, так как в этом случае напряжение питания оказывается недостаточным для срабатывания, поэтому tтр=∞.
Максимальное время трогания получают из (6.34), считая Qн=∞:
![]() (6.36)
(6.36)
Максимально возможное время можно получить из (6.36) при kiтр=1: tтрmax=3/(4f).
Если пренебречь активным сопротивлением обмотки и считать, что электромагнитное усилие пропорционально квадрату потока (по формуле Максвелла), а противодействующее усилие постоянно, то для периода движения уравнения динамики будут иметь вид
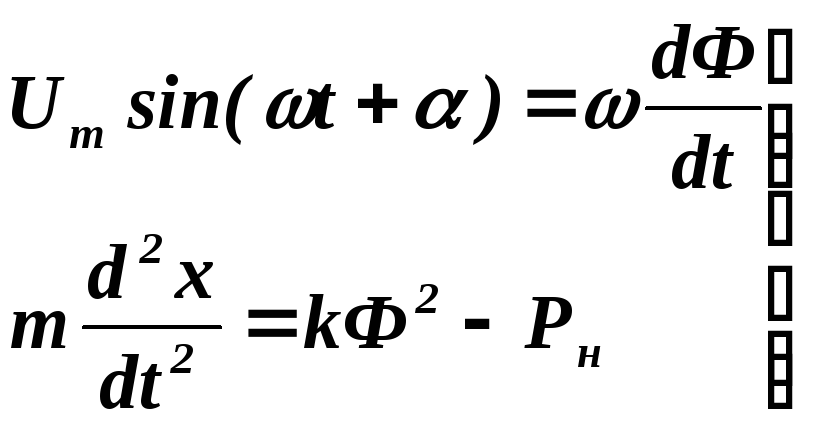 (6.37)
(6.37)
где k =1/(6μ0S). Совместное их решение позволяет получить зависимость хода якоря от времени.
Учитывая, что при t=tдв ход якоря равен разности начального и конечного рабочих зазоров, т.е. х=δн-δк можно получить приближенное выражение для определения времени движения якоря электромагнита переменного тока:
![]() (6.38)
(6.38)
где
![]()
Для электромагнитов переменного тока характерна слабая зависимость электромагнитной силы от величины рабочего воздушного зазора. Это определяется в основном тем, что с изменением воздушного зазора меняется индуктивное электрическое сопротивление обмотки электромагнита, которое в простейшем случае (без учета рассеяния, магнитного сопротивления стали и при равномерном магнитном поле в рабочем воздушном зазоре):
![]() ,
(6.39)
,
(6.39)
где w ‑ число витков обмотки; S и δ ‑ площадь полюса и рабочий воздушный зазор.
Выражая при заданном напряжении U ток в обмотке i=U/x=Uδ/ωw2μ0S находим выражение для электромагнитной силы:
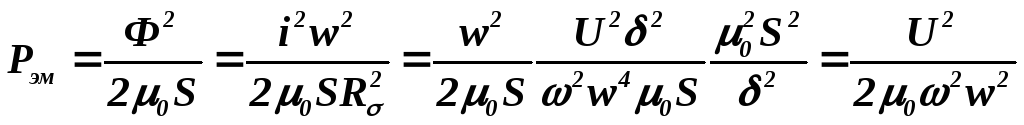 (6-40)
(6-40)
В принятых условиях электромагнитная сила электромагнита переменного тока не зависит от величины рабочего воздушного зазора. В реальных условия, в основном из-за отвлечения части магнитного потока в рассеяние, электромагнитная сила в рабочем зазоре несколько уменьшается при его увеличении; с увеличением воздушного рабочего зазора потоки рассеяния увеличиваются.
Электромагниты переменного тока имеют ряд недостатков, отсутствующих у электромагнитов постоянного тока:
а) при заданной площади полюса средняя сила тяги вдвое меньше, чем у электромагнитов постоянного тока;
б) каждая единица производимой работы требует определенной реактивной мощности, растущей пропорционально частоте питающего напряжения; отсюда вытекает также и сильная зависимость тяговых характеристик от частоты;
в) конструктивное выполнение электромагнитов ограничено из-за необходимости выполнения магнитопровода шихтованным из тонколистовой электротехнической стали;
г) дополнительный нагрев магнитопровода в результате потерь в нем и в короткозамкнутом витке;
д) слабо возрастающая по ходу якоря тяговая характеристика во многих случаях ограничивает возможности согласования ее с нагрузочной характеристикой.
е) низкая устойчивость при механических воздействия из-за повышенного веса подвижных частей и малой избыточной силы электромагнита при притянутом якоре.
