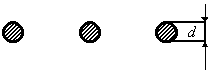- •Варфоломеева а.С., Кургузов н.Н., Кургузова л.И., Леньков ю.А., Никитин к.И.
- •Учебное пособие. Омск: Изд-во ОмГту, 2007. 197 с.
- •Содержание
- •Введение
- •1 Нагревание проводников и электрических аппаратов
- •1.1 Допустимые максимальные температуры электрических аппаратов и проводников в нормальном режиме и при коротком замыкании
- •1.1.1Общие сведения
- •1.1.2 Изолированные проводники электрического тока в нормальном режиме
- •1.1.3 Неизолированные токоведущие части аппаратов в нормальном режиме
- •1.1.4 Изолированные и неизолированные токоведущие части аппаратов при коротких замыканиях
- •1.1.5 Нетоковедущие части аппаратов
- •1.2 Нагрев проводников и аппаратов
- •1.2.1 Общие сведения
- •1.2.2 Активные потери энергии в проводниках и электрических аппаратах
- •1.2.2.1 Потери в токоведущих частях
- •1.2.2.2 Потери в нетоковедущих ферромагнитных деталях аппаратов
- •1.2.2.3 Потери в диэлектриках
- •1.3 Способы передачи тепла внутри нагретых тел и с их поверхности
- •1.4 Установившийся режим нагрева проводников и аппаратов
- •1.4.1 Общие сведения
- •1.4.2 Тепловой расчёт неизолированных проводников в установившемся режиме
- •1.4.3 Тепловой расчёт изолированных проводников и кабелей
- •1.4.4 Нагревание аппаратов в установившимся режиме
- •1.4.5 Выбор проводников и аппаратов по условиям продолжительного режима
- •1.5 Нагрев проводников и аппаратов в переходных режимах
- •1.6 Примеры теплового расчета
- •Задание №1
- •2 Термическая и электродинамическая стойкость электрических проводников и аппаратов
- •2.1 Нагрев проводников и аппаратов при коротком замыкании
- •2.2 Термическая стойкость проводников и аппаратов
- •2.2.1 Термическая стойкость неизолированных проводников
- •2.2.2 Термическая стойкость кабелей
- •2.2.3 Термическая стойкость электрических аппаратов
- •2.3 Определение импульса квадратичного тока короткого замыкания
- •2.4 Электродинамические усилия в электрических проводниках и аппаратах
- •2.4.1 Общие сведения
- •2.4.2 Методы расчёта электродинамических усилий
- •2.4.3 Усилия между параллельными проводниками
- •2.4.4 Усилия и моменты, действующие на взаимно перпендикулярные проводники
- •2.5 Электродинамические силы в трёхфазной шинной линии при различных видах короткого замыкания
- •2.5.1 Общие сведения
- •2.5.2 Электродинамические силы в трёхфазной шинной линии при трёхфазном коротком замыкании
- •2.5.3 Электродинамические силы в трёхфазной шинной линии при двухфазном коротком замыкании
- •2.6 Электродинамическая стойкость проводников и электрических аппаратов
- •2.6.1 Электродинамическая стойкость проводников
- •2.6.2 Электродинамическая стойкость аппаратов
- •2.7 Примеры расчета термической и электродинамической стойкости проводников и аппаратов
- •Задание №2
- •3 Электрические контакты
- •3.1 Назначения и требования к электрическим контактам
- •3.2 Сопротивление электрического контакта
- •3.3 Нагрев контактных соединений
- •3.3.1 Нагрев контактных соединений при номинальном токе
- •3.3.2 Нагрев контактных соединений при токах короткого замыкания
- •3.4 Конструкция контактных соединений и контактов
- •3.5 Пример расчета нагрева контактных соединений
- •Задание №3.
- •4 Отключение цепей постоянного и переменного тока
- •4.1 Общие сведения
- •4.2 Электрическая дуга
- •4.3 Возбуждение атома.
- •4.4 Ионизация
- •4.4.1 Термоэлектронная эмиссия.
- •4.4.2 Автоэлектронная (электростатическая) эмиссия.
- •4.4.3 Ионизация столкновением
- •4.5 Ударная ионизация
- •4.6 Термическая диссоциация и ионизация.
- •4.7 Деионизация дугового промежутка осуществляется путем рекомбинации и диффузии.
- •4.7.1 Рекомбинация (воссоединение)
- •4.8 Диффузия
- •4.9. Подвижностью ионов (электронов)
- •4.10 Радиационный захват электрона
- •4.11 Классификация дуг
- •4.11.1 Область катодного падения напряжения
- •4.11.2 Область анодного падения напряжения.
- •4.11.3 Ствол дуги
- •4.11.4 Турбулентная конвекция.
- •4.11.5 Баланс энергии в стволе дуги.
- •4.12 Потоки плазмы в дуге
- •4.13 Воздействие внешнего магнитного поля
- •4.14 Дуга постоянного тока и ее характеристики
- •4.15 0Тключение электрических цепей постоянного тока
- •4.15.1 Условия стабильного горения и гашения дуги
- •4.15.2 Открытый разрыв
- •4.15.3 Дугогасительные устройства с узкой щелью
- •4.15.4 Дугогасительные решетки
- •4.15.5 Гашение дуги под воздействием магнитного поля
- •4.16 Электрическая дуга переменного тока и ее характеристики
- •4.17 Отключение электрических цепей переменного тока
- •4.17.1 Отключение активной цепи переменного тока
- •4.17.2.Отключение индуктивной цепи переменного тока
- •4.18 Гашение электрической дуги в выключателях переменного тока
- •4.18.1 Гашение электрической дуги в потоке сжатого воздуха
- •4.18.2 Гашение электрической дуги в элегазе
- •4.18.3 Гашение электрической дуги в трансформаторном масле
- •4.18.4 Гашение электрической дуги в вакууме
- •4.18.5 Гашение электрической дуги с помощью электромагнитного поля
- •4.19 Примеры расчета отключения цепей постоянного и переменного тока
- •Задание №4
- •5 Восстанавливающееся напряжение на контактах выключателя
- •5.1 Параметры восстанавливающегося напряжения
- •5.2 Расчет параметров восстанавливающегося напряжения в однофазной системе
- •5.3 Расчет параметров восстанавливающегося напряжения в трехфазных эффективно-заземленных сетях
- •5.4 Вторая стадия переходного процесса
- •5.5 Номинальные характеристики пвн
- •5.6 Пример расчета параметров пвн на полюсах выключателя
- •6 Электромагниты
- •6.1Электромагниты постоянного тока
- •6.2 Поляризованные электромагниты и постоянные магниты
- •6.3 Электромагниты переменного тока
- •6.4 Примеры расчета электромагнитов
- •1‑Основание; 2‑сердечник; 3‑полюсный наконечник; 4‑якорь
- •Задание №5
- •1 ‑ Якорь; 2 ‑ фланец верхний; 3 ‑ корпус; 4 ‑ фланец нижний; 5 ‑ стоп; 6 ‑ латунная втулка
- •1 ‑ Фланец верхний; 2 ‑ якорь; 3 ‑ стоп; 4 ‑ корпус; 5 ‑ фланец нижний
- •1 ‑ Фланец верхний; 2 ‑ якорь; 3 ‑ стоп; 4 ‑ корпус; 5 ‑ фланец нижний
- •1 ‑ Основание; 2 ‑ сердечник; 3 ‑ полюсный наконечник; 4 ‑ якорь
- •1 ‑ Якорь; 2 ‑ основание; 3 ‑ сердечник; 4 – катушка
- •1 ‑ Якорь; 2 ‑ верхняя плита; 3 ‑ нижняя плита; 4 – полюс.
- •Литература
- •Приложение
2.6 Электродинамическая стойкость проводников и электрических аппаратов
2.6.1 Электродинамическая стойкость проводников
Сборные шины и ошиновка распределительных устройств электрических станций и подстанций должны обладать достаточной механической прочностью, чтобы противостоять механическим усилиям, возникающим при КЗ.
Динамическую
стойкость любой шинной конструкции
рассчитывают по наибольшему значению
механического напряжения в шине
![]() и наибольшему значению силы,
действующей на головку изолятора
и наибольшему значению силы,
действующей на головку изолятора
![]() .
.
Напряжение
![]() в материале, однополосных шин, расположенных
в одной плоскости, при трехфазном или
двухфазном КЗ определяется согласно
[2] по формуле:
в материале, однополосных шин, расположенных
в одной плоскости, при трехфазном или
двухфазном КЗ определяется согласно
[2] по формуле:
![]() ,
(2.46)
,
(2.46)
где Fмакс
- максимальная сила, действующая на
расчетную фазу при трехфазном или
двухфазном КЗ, Н; l
- длина пролета, м; W
- момент сопротивления шины относительно
оси, перпендикулярной действию усилия,
м3 (таблица 2.6);
![]() - коэффициент, зависящий от условия
закрепления шин и числа пролетов,
определяемый по [2] или по таблице 2.7;
- коэффициент, зависящий от условия
закрепления шин и числа пролетов,
определяемый по [2] или по таблице 2.7;
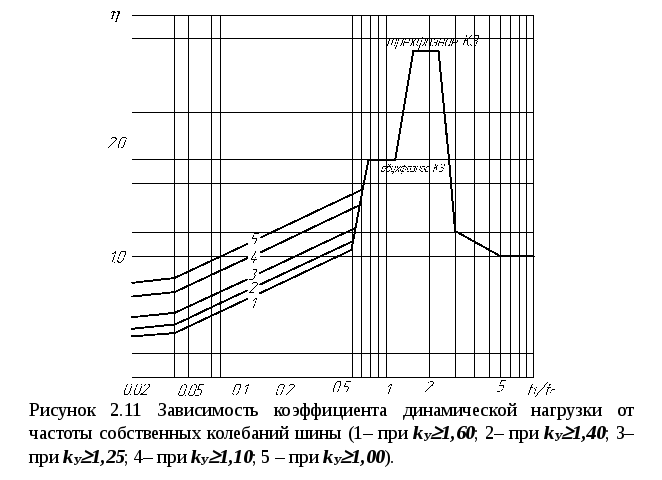
![]() - коэффициент динамической нагрузки
шин и изоляторов, определяемый по кривым,
приведенным в [2] или на рисунке 2.11.
- коэффициент динамической нагрузки
шин и изоляторов, определяемый по кривым,
приведенным в [2] или на рисунке 2.11.
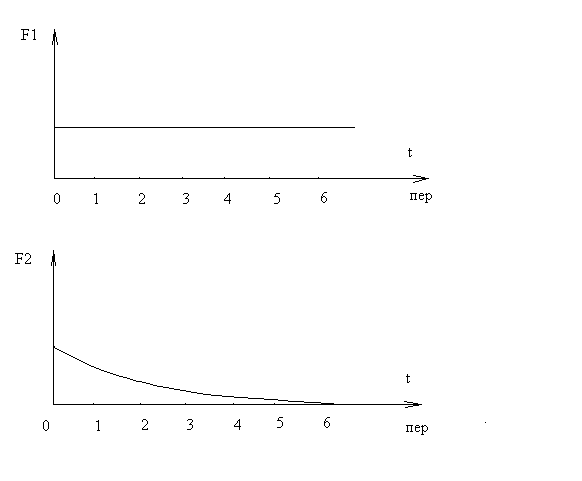
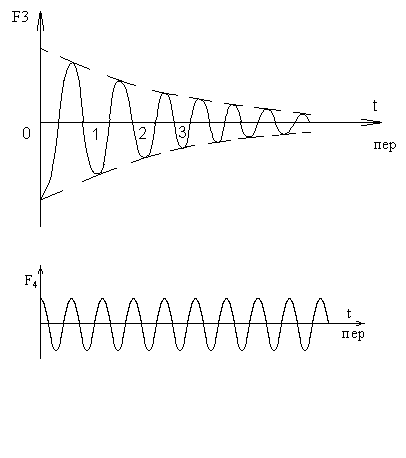
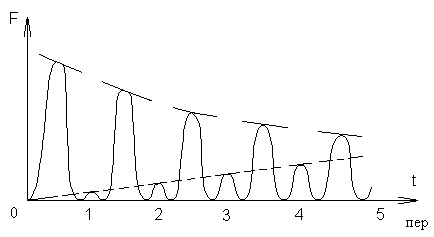
Рис. 2.10 - Осциллограммы электродинамических сил при двухфазном коротком замыкании
Максимальная сила
![]() ,
действующая при трехфазном или двухфазном
КЗ на расчетную фазу определяется по
формулам
,
действующая при трехфазном или двухфазном
КЗ на расчетную фазу определяется по
формулам
![]() ;
;
(2.47)
![]() ,
,
Таблица 2.6
Моменты сопротивления и инерции шин
|
Расположение шин |
Момент
инерции
|
Момент сопротивления
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где
![]() - расстояние между соседними фазами, м;
- расстояние между соседними фазами, м;
![]() - ударный ток трехфазного тока КЗ, А;
- ударный ток трехфазного тока КЗ, А;
![]() - ударный ток двухфазного тока КЗ, А;
- ударный ток двухфазного тока КЗ, А;
![]() - длина пролета, м;
- длина пролета, м;
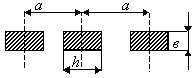
![]() - коэффициент формы шины прямоугольного
сечения определяемый по кривым рисунка
2.7. Если расстояние в свету между
проводниками прямоугольной формы больше
периметра поперечного сечения токоведущей
части, т.е.
- коэффициент формы шины прямоугольного
сечения определяемый по кривым рисунка
2.7. Если расстояние в свету между
проводниками прямоугольной формы больше
периметра поперечного сечения токоведущей
части, т.е.
![]() ,
то
,
то
![]() .
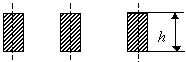
Для шин корытного сечения с высотой
сечения
.
Для шин корытного сечения с высотой
сечения
![]() коэффициент формы шин
коэффициент формы шин
![]() ,
при
,
при
![]() коэффициент формы
коэффициент формы
![]() ,
а при
,
а при
![]() коэффициент формы
коэффициент формы
![]() .
Для проводников кольцевого сечения и
круглых проводников сплошного сечения
коэффициент формы
.
Для проводников кольцевого сечения и
круглых проводников сплошного сечения
коэффициент формы
![]() ;
;
![]() - коэффициент, зависящий от взаимного
расположения шин определяемый по [2] или
таблице 2.8.
- коэффициент, зависящий от взаимного
расположения шин определяемый по [2] или
таблице 2.8.
Расчетная фаза зависит от взаимного расположения шин, таблица 2.7.
Таблица 2.7
Расчетные схемы шинных конструкций
|
Расчетная схема |
Тип балки |
Коэффициенты |
||
|
|
|
|
||
|
|
Балка с одним пролетом |
8,00 |
1,00 |
3,14 |
|
|
Балка с двумя пролетами |
8,00 |
1,25 |
3,93 |
|
|
Балка с тремя и более пролетами для крайних пролетов для средних пролетов |
10,00 12,00 |
1,13 1,00 |
4,73 4,73 |
Для определения
динамического коэффициента
![]() ,
необходимо рассчитать частоту собственных
колебаний шины
,
необходимо рассчитать частоту собственных
колебаний шины
![]() и определить отношение
и определить отношение
![]() ,
где
,
где
![]() Гц.
Частота собственных колебаний шины
определяется согласно [2] по формуле
Гц.
Частота собственных колебаний шины
определяется согласно [2] по формуле
![]() ,
(2.48)
,
(2.48)
где
![]() - параметр основной собственной частоты
шины, который зависит от типа шинной
конструкции и определяется по таблице
2.7;
- параметр основной собственной частоты
шины, который зависит от типа шинной
конструкции и определяется по таблице
2.7;
![]() - модуль упругости материала шин (таблица
2.9), Па;
- модуль упругости материала шин (таблица
2.9), Па;
![]() - момент инерции поперечного сечения
шины определяемый по формулам таблицы
2.6, м4;
- момент инерции поперечного сечения
шины определяемый по формулам таблицы
2.6, м4;
![]() - масса шины на единицу длины, кг/м;
- масса шины на единицу длины, кг/м;
![]() - плотность материала шины, кг/м3,
таблица 2.9;
- плотность материала шины, кг/м3,
таблица 2.9;
![]() - поперечное сечение шины, м2.
- поперечное сечение шины, м2.
Однополосные шины механически прочны, если
![]() ,
(2.49)
,
(2.49)
где
![]() ‑ допустимое механическое
напряжение в материале шин, таблица
2.9.
‑ допустимое механическое
напряжение в материале шин, таблица
2.9.
Если условие (2.49) не выполняется, то необходимо определить допустимую длину пролета по формуле
![]() (2.50)
(2.50)
и повторить расчет.
Таблица 2.8
Значения коэффициента
![]()
|
Расположение шин |
Расчетная фаза |
Значения
коэффициента
для нагрузок |
|||
|
|
|
результи-рующей |
изгиба-ющей |
растяги-вающей |
сжимаю-щей |
|
В одной плоскости (рис. 4.4) |
В |
1,00 |
1,00 |
0 |
0 |
|
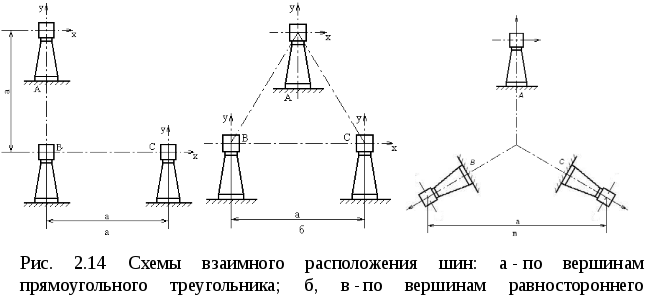
По вершинам равностороннего треугольника (рис. 2.14,а) |
А, С
В |
1,00
1,00 |
0,94
0,50 |
0,25
1,00 |
0,75
0 |
|
По вершинам прямоугольного треугольника (рис. 2.14,б) |
А В С |
0,87 0,95 0,95 |
0,87 0,43 0,93 |
0,29 0,83 0,14 |
0,87 0,07 0,43 |
|
По вершинам равностороннего треугольника (рис. 2.14,в) |
А, В, С |
1,00 |
0,50 |
1,00 |
0 |
Таблица 2.9
Характеристики материалов шин
|
Мате-риал шины |
Марка |
Временное сопротивление разрыву |
Допустимое напряжение
|
Модуль
упруго-сти Па |
Плот-ность мате-риала
кг/м3 |
||
|
мате-риала |
сварно-го шва |
мате- риала |
сварно-го шва |
||||
|
Алюминий |
АО, А |
118 |
118 |
82 |
82 |
7 |
2710 |
|
АДО |
59-69 |
59-69 |
41-48 |
41-48 |
7 |
2710 |
|
|
Алюминиевый сплав |
АД31Т |
127 |
120 |
89 |
84 |
7 |
2710 |
|
АД31Т1 |
196 |
120 |
137 |
84 |
7 |
2710 |
|
|
АВТ1 |
304 |
152 |
213 |
106 |
7 |
2700 |
|
|
АВТ |
- |
- |
144 |
- |
7 |
2700 |
|
|
1915Т |
353 |
318 |
247 |
223 |
7 |
2700 |
|
|
Медь |
МГМ |
245-255 |
- |
171,5-178 |
- |
10 |
8900 |
|
МГТ |
245-294 |
|
171,5-206 |
- |
10 |
8900 |
|
При расчете
двухполосных шин необходимо определять
две составляющие механического напряжения
в материале:
![]() от взаимодействия пакетов разных фаз
и
от взаимодействия пакетов разных фаз
и
![]() от взаимодействия полос внутри одного
пакета.
от взаимодействия полос внутри одного
пакета.
Двухполосные шины механически прочны, если
![]() .
(2.51)
.
(2.51)
Напряжение в
материале шин от взаимодействия пакетов
различных фаз
![]() определяется по формуле (2.46).
определяется по формуле (2.46).
Механическое
напряжение в материале шин от взаимодействия
полос пакета
![]() ,
определяется согласно [2]
по формуле
,
определяется согласно [2]
по формуле
![]() ,
(2.52)
,
(2.52)
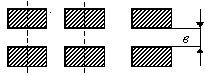
где
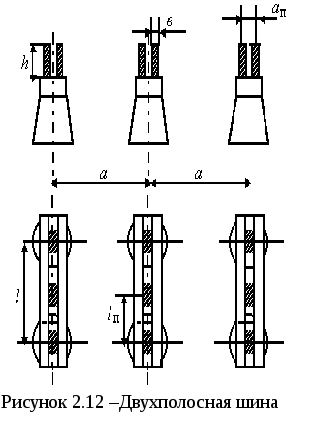
![]() - расстояние между прокладками (рис.
2.12), м;
- расстояние между прокладками (рис.
2.12), м;
![]() - расстояние между осями шин пакета
(рис. 2.12), м;
- расстояние между осями шин пакета
(рис. 2.12), м;
![]() - ударный ток трехфазного или двухфазного
КЗ, А;
- ударный ток трехфазного или двухфазного
КЗ, А;
![]() - момент сопротивления полосы пакета
относительно оси, перпендикулярной к
направлению действия силы, м3;
- момент сопротивления полосы пакета
относительно оси, перпендикулярной к
направлению действия силы, м3;
![]() - число полос в пакете фазы;
- число полос в пакете фазы;
![]() - коэффициент динамической нагрузки,
который зависит от основной частоты
собственных колебаний шин пакета
- коэффициент динамической нагрузки,
который зависит от основной частоты
собственных колебаний шин пакета
![]() и определяется по кривым рис. 2.11.
и определяется по кривым рис. 2.11.
Основная частота собственных колебаний шины пакета в соответствии с [2] определяется по формуле
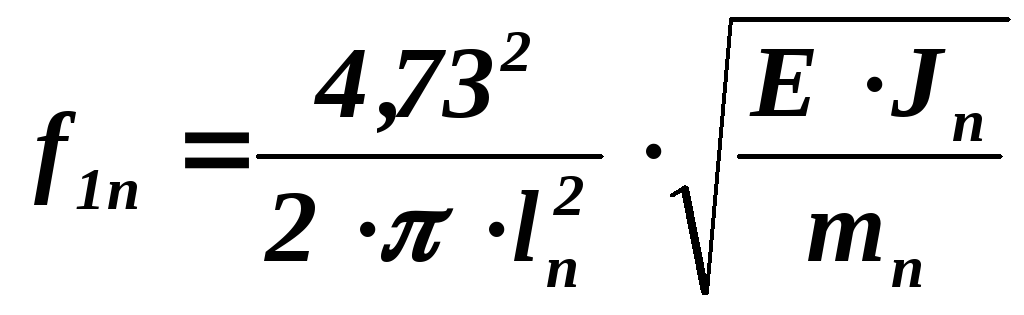 ,
(2.53)
,
(2.53)
где
![]() - момент инерции поперечного сечения
шины пакета, м4;
- момент инерции поперечного сечения
шины пакета, м4;
![]() - расстояние между прокладками, м;
- расстояние между прокладками, м;
![]() - масса шины пакета на единицу длины,
кг/м.
- масса шины пакета на единицу длины,
кг/м.
Если шины распределительного устройства выполняются из шин коробчатого сечения, то механическое напряжение в материале шин от взаимодействия фаз определяется по (2.46) с учетом расположения шин.
При расположении
шин в горизонтальной плоскости, рис.
2.13, а, и соединении швеллеров между собой
жестко,
![]() .
При отсутствии жесткого соединения
.
При отсутствии жесткого соединения
![]() .
.
При расположении
шин в вертикальной плоскости, рис.
2.13,б,
![]() .
.
Значения
![]() и
и
![]() берутся из таблицы 7.6 9.
берутся из таблицы 7.6 9.
Механическое напряжение п в материале шин от взаимодействия между швеллерами одной фазы определяется по выражению (2.52).
Шины коробчатого сечения механически прочны, если выполняется условие (2.51).
Если условие (2.51) не соблюдается, то необходимо уменьшить ф или п, уменьшив при этом, соответственно, l или lп.
Величина пролёта l определяется конструкцией распределительного устройства, а величину lп можно изменять, увеличивая число прокладок в пролете, если швеллеры не соединены жестко по всей длине.
В том случае если сборные шины распределительных устройств располагаются по вершинам треугольника, рис. 2.14, максимальное механическое напряжение в материале шин макс определяется по формуле
![]() ,
(2.54)
,
(2.54)
где
![]() - меньший из двух моментов сопротивлений
поперечного сечения шины
- меньший из двух моментов сопротивлений
поперечного сечения шины
![]() или
или
![]() ,
м3;
,
м3;
![]() - электродинамические силы, определяемые
по (2.46) или (2.47);
- электродинамические силы, определяемые
по (2.46) или (2.47);
![]() - коэффициент, значение которого для
шинных конструкций расположенных по
вершинам треугольников приведено в [2]
и в таблице 2.10.
- коэффициент, значение которого для
шинных конструкций расположенных по
вершинам треугольников приведено в [2]
и в таблице 2.10.
Жесткие шины распределительных устройств закрепятся на опорных изоляторах, которые выбираются из условий
![]() ,
(2.55)
,
(2.55)
где
![]() – номинальное напряжение установки;
– номинальное напряжение установки;
![]() – номинальное напряжение изолятора;
– номинальное напряжение изолятора;
![]() – сила, действующая на изолятор;
– сила, действующая на изолятор;
![]() – допустимая нагрузка на головку
изолятора.
– допустимая нагрузка на головку
изолятора.
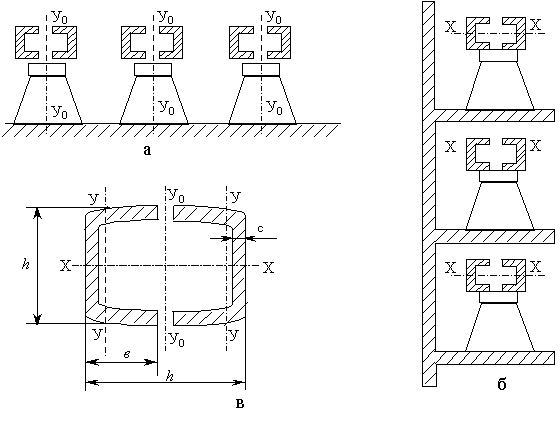
Рис. 2.13 - Эскиз расположения шин коробчатого сечения; а ‑ горизонтальное расположение; б ‑ вертикальное расположение; в ‑ сечение коробчатой шины
При расположении сборных шин в горизонтальной или вертикальной плоскости расчетная нагрузка, действующая на изоляторы, обладающие высокой жесткостью, определяется по выражению [2]:
![]() ,
(2.56)
,
(2.56)
где![]() - коэффициент, зависящий от условия
крепления шин, а также числа пролетов
конструкции с неразрезанными шинами и
определяется по таблице 2.7;
- коэффициент, зависящий от условия
крепления шин, а также числа пролетов
конструкции с неразрезанными шинами и
определяется по таблице 2.7;
![]() - максимальная сила, возникающая в
многопролетной шине при трехфазном или
двухфазном КЗ, Н;
- максимальная сила, возникающая в
многопролетной шине при трехфазном или
двухфазном КЗ, Н;
![]() - коэффициент динамической нагрузки,
определяемый по кривым рисунка 2.11.
- коэффициент динамической нагрузки,
определяемый по кривым рисунка 2.11.
Максимальная нагрузка, действующая на проходные изоляторы при КЗ, определяется по формуле
![]() ,
(2.57)
,
(2.57)
где
![]() - расстояние от торца проходного изолятора
до ближайшего опорного изолятора фазы,
м.
- расстояние от торца проходного изолятора
до ближайшего опорного изолятора фазы,
м.
Максимальная нагрузка, действующая на опорные и проходные изоляторы, при расположении шин по вершинам треугольника в соответствии с [2] определяется по формуле
![]() ,
(2.58)
,
(2.58)
где
![]() - максимальная сила, действующая на
изоляторы при трехфазном или двухфазном
КЗ, которая определяется по формулам
(2.47);
- максимальная сила, действующая на
изоляторы при трехфазном или двухфазном
КЗ, которая определяется по формулам
(2.47);
![]() - коэффициент, значение которого приведено
в таблице 2.10, для наиболее распространенных
типов шинных конструкций.
- коэффициент, значение которого приведено
в таблице 2.10, для наиболее распространенных
типов шинных конструкций.
Таблица 2.10
Значения коэффициентов
![]() и
и
![]() шинных конструкций, расположенных по
вершинам треугольника
шинных конструкций, расположенных по
вершинам треугольника
|
Расположение шин |
Коэффициент
|
Коэффициент
|
|
|
Шины круглого и кольцевого сечения |
Шины квадратного сечения |
||
|
По вершинам прямоугольного треугольника (рис. 2.14,а) |
0,95 |
0,95 |
1,16 |
|
По вершинам равностороннего треугольника (рис. 2.14,б) |
1,00 |
1,00 |
1,39 |
|
По вершинам равностороннего треугольника (рис. 2.14,в) |
1,00 |
1,00 |
1,21 |
Д
Рисунок 2.15 К
определению допустимых нагрузок на
опорные изоляторы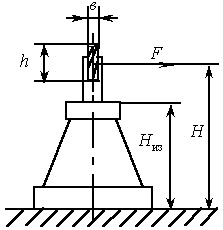
![]() ,
действующая на опорный изолятор рис.
2.15, определяется по формуле
,
действующая на опорный изолятор рис.
2.15, определяется по формуле
![]() ,
(2.59)
,
(2.59)
где
![]() - минимальная разрушающая сила на изгиб
изолятора, задаваемая заводом-изготовителем,
Н;
- минимальная разрушающая сила на изгиб
изолятора, задаваемая заводом-изготовителем,
Н;
![]() - высота изолятора, рис. 2.15, мм;
- высота изолятора, рис. 2.15, мм;
![]() -
высота шины, мм.
-
высота шины, мм.