
- •Варфоломеева а.С., Кургузов н.Н., Кургузова л.И., Леньков ю.А., Никитин к.И.
- •Учебное пособие. Омск: Изд-во ОмГту, 2007. 197 с.
- •Содержание
- •Введение
- •1 Нагревание проводников и электрических аппаратов
- •1.1 Допустимые максимальные температуры электрических аппаратов и проводников в нормальном режиме и при коротком замыкании
- •1.1.1Общие сведения
- •1.1.2 Изолированные проводники электрического тока в нормальном режиме
- •1.1.3 Неизолированные токоведущие части аппаратов в нормальном режиме
- •1.1.4 Изолированные и неизолированные токоведущие части аппаратов при коротких замыканиях
- •1.1.5 Нетоковедущие части аппаратов
- •1.2 Нагрев проводников и аппаратов
- •1.2.1 Общие сведения
- •1.2.2 Активные потери энергии в проводниках и электрических аппаратах
- •1.2.2.1 Потери в токоведущих частях
- •1.2.2.2 Потери в нетоковедущих ферромагнитных деталях аппаратов
- •1.2.2.3 Потери в диэлектриках
- •1.3 Способы передачи тепла внутри нагретых тел и с их поверхности
- •1.4 Установившийся режим нагрева проводников и аппаратов
- •1.4.1 Общие сведения
- •1.4.2 Тепловой расчёт неизолированных проводников в установившемся режиме
- •1.4.3 Тепловой расчёт изолированных проводников и кабелей
- •1.4.4 Нагревание аппаратов в установившимся режиме
- •1.4.5 Выбор проводников и аппаратов по условиям продолжительного режима
- •1.5 Нагрев проводников и аппаратов в переходных режимах
- •1.6 Примеры теплового расчета
- •Задание №1
- •2 Термическая и электродинамическая стойкость электрических проводников и аппаратов
- •2.1 Нагрев проводников и аппаратов при коротком замыкании
- •2.2 Термическая стойкость проводников и аппаратов
- •2.2.1 Термическая стойкость неизолированных проводников
- •2.2.2 Термическая стойкость кабелей
- •2.2.3 Термическая стойкость электрических аппаратов
- •2.3 Определение импульса квадратичного тока короткого замыкания
- •2.4 Электродинамические усилия в электрических проводниках и аппаратах
- •2.4.1 Общие сведения
- •2.4.2 Методы расчёта электродинамических усилий
- •2.4.3 Усилия между параллельными проводниками
- •2.4.4 Усилия и моменты, действующие на взаимно перпендикулярные проводники
- •2.5 Электродинамические силы в трёхфазной шинной линии при различных видах короткого замыкания
- •2.5.1 Общие сведения
- •2.5.2 Электродинамические силы в трёхфазной шинной линии при трёхфазном коротком замыкании
- •2.5.3 Электродинамические силы в трёхфазной шинной линии при двухфазном коротком замыкании
- •2.6 Электродинамическая стойкость проводников и электрических аппаратов
- •2.6.1 Электродинамическая стойкость проводников
- •2.6.2 Электродинамическая стойкость аппаратов
- •2.7 Примеры расчета термической и электродинамической стойкости проводников и аппаратов
- •Задание №2
- •3 Электрические контакты
- •3.1 Назначения и требования к электрическим контактам
- •3.2 Сопротивление электрического контакта
- •3.3 Нагрев контактных соединений
- •3.3.1 Нагрев контактных соединений при номинальном токе
- •3.3.2 Нагрев контактных соединений при токах короткого замыкания
- •3.4 Конструкция контактных соединений и контактов
- •3.5 Пример расчета нагрева контактных соединений
- •Задание №3.
- •4 Отключение цепей постоянного и переменного тока
- •4.1 Общие сведения
- •4.2 Электрическая дуга
- •4.3 Возбуждение атома.
- •4.4 Ионизация
- •4.4.1 Термоэлектронная эмиссия.
- •4.4.2 Автоэлектронная (электростатическая) эмиссия.
- •4.4.3 Ионизация столкновением
- •4.5 Ударная ионизация
- •4.6 Термическая диссоциация и ионизация.
- •4.7 Деионизация дугового промежутка осуществляется путем рекомбинации и диффузии.
- •4.7.1 Рекомбинация (воссоединение)
- •4.8 Диффузия
- •4.9. Подвижностью ионов (электронов)
- •4.10 Радиационный захват электрона
- •4.11 Классификация дуг
- •4.11.1 Область катодного падения напряжения
- •4.11.2 Область анодного падения напряжения.
- •4.11.3 Ствол дуги
- •4.11.4 Турбулентная конвекция.
- •4.11.5 Баланс энергии в стволе дуги.
- •4.12 Потоки плазмы в дуге
- •4.13 Воздействие внешнего магнитного поля
- •4.14 Дуга постоянного тока и ее характеристики
- •4.15 0Тключение электрических цепей постоянного тока
- •4.15.1 Условия стабильного горения и гашения дуги
- •4.15.2 Открытый разрыв
- •4.15.3 Дугогасительные устройства с узкой щелью
- •4.15.4 Дугогасительные решетки
- •4.15.5 Гашение дуги под воздействием магнитного поля
- •4.16 Электрическая дуга переменного тока и ее характеристики
- •4.17 Отключение электрических цепей переменного тока
- •4.17.1 Отключение активной цепи переменного тока
- •4.17.2.Отключение индуктивной цепи переменного тока
- •4.18 Гашение электрической дуги в выключателях переменного тока
- •4.18.1 Гашение электрической дуги в потоке сжатого воздуха
- •4.18.2 Гашение электрической дуги в элегазе
- •4.18.3 Гашение электрической дуги в трансформаторном масле
- •4.18.4 Гашение электрической дуги в вакууме
- •4.18.5 Гашение электрической дуги с помощью электромагнитного поля
- •4.19 Примеры расчета отключения цепей постоянного и переменного тока
- •Задание №4
- •5 Восстанавливающееся напряжение на контактах выключателя
- •5.1 Параметры восстанавливающегося напряжения
- •5.2 Расчет параметров восстанавливающегося напряжения в однофазной системе
- •5.3 Расчет параметров восстанавливающегося напряжения в трехфазных эффективно-заземленных сетях
- •5.4 Вторая стадия переходного процесса
- •5.5 Номинальные характеристики пвн
- •5.6 Пример расчета параметров пвн на полюсах выключателя
- •6 Электромагниты
- •6.1Электромагниты постоянного тока
- •6.2 Поляризованные электромагниты и постоянные магниты
- •6.3 Электромагниты переменного тока
- •6.4 Примеры расчета электромагнитов
- •1‑Основание; 2‑сердечник; 3‑полюсный наконечник; 4‑якорь
- •Задание №5
- •1 ‑ Якорь; 2 ‑ фланец верхний; 3 ‑ корпус; 4 ‑ фланец нижний; 5 ‑ стоп; 6 ‑ латунная втулка
- •1 ‑ Фланец верхний; 2 ‑ якорь; 3 ‑ стоп; 4 ‑ корпус; 5 ‑ фланец нижний
- •1 ‑ Фланец верхний; 2 ‑ якорь; 3 ‑ стоп; 4 ‑ корпус; 5 ‑ фланец нижний
- •1 ‑ Основание; 2 ‑ сердечник; 3 ‑ полюсный наконечник; 4 ‑ якорь
- •1 ‑ Якорь; 2 ‑ основание; 3 ‑ сердечник; 4 – катушка
- •1 ‑ Якорь; 2 ‑ верхняя плита; 3 ‑ нижняя плита; 4 – полюс.
- •Литература
- •Приложение
2.4 Электродинамические усилия в электрических проводниках и аппаратах
2.4.1 Общие сведения
Известно, что электрические токи взаимодействуют. Силы взаимодействия проводников с током принято называть электродинамическими силами [3].Действию электродинамических сил подвержены все элементы электрических систем, в том числе токопроводы и электрические аппараты. Для предотвращения механических повреждений, под действием этих сил, все элементы токоведущей конструкции должны обладать достаточной электродинамической стойкостью.
Под электродинамической стойкостью понимают способность аппарата или проводника противостоять электродинамическим силам, возникающим при протекании токов КЗ.
2.4.2 Методы расчёта электродинамических усилий
Для расчета
электродинамических усилий используются
два метода [2]. В первом методе
электродинамические усилия определяются
как результат взаимодействия проводника
с током и магнитным полем. Если элементарный
проводник
![]() с током
с током
![]() находится в магнитном поле с индукцией
находится в магнитном поле с индукцией
![]() ,
создаваемой другим проводником, то сила
,
создаваемой другим проводником, то сила
![]() ,
действующая на этот элемент, равна:
,
действующая на этот элемент, равна:
![]() ,
(2.20)
,
(2.20)
где
![]() -
угол между векторами элемента
-
угол между векторами элемента
![]() и
индукции
и
индукции
![]() .
За направление
.
За направление
![]() принимается
направление тока в этом элементе.
принимается
направление тока в этом элементе.
Для определения
полного электродинамического усилия,
действующего на проводник длиной
![]() ,
необходимо просуммировать усилия,
действующие на все его элементы:
,
необходимо просуммировать усилия,
действующие на все его элементы:
![]() .
(2.21)
.
(2.21)
Второй метод определения электродинамических усилий основан на использовании закона сохранения энергии. Если принять, что величина тока в токоведущих контурах остается неизменной при их перемещении под действием электродинамических усилий, то силу можно определить по уравнению:
![]() ,
(2.22)
,
(2.22)
где
![]() – электромагнитная энергия;
– электромагнитная энергия;
![]() - возможное перемещение в направлении
действия силы
- возможное перемещение в направлении
действия силы
![]() .
.
Таким образом, сила равна частной производной от электромагнитной энергии данной системы по координате, в направлении которой она действует. Электромагнитная энергия системы обусловлена как энергией магнитного поля каждого изолированного контура, так и энергией, определяемой магнитной связью между контурами.
Для системы трех взаимосвязанных контуров электромагнитная энергия равна:
![]() ,
(2.23)
,
(2.23)
где L1, L2, L3– индуктивности контуров; i1, i2, i3– токи в контурах; M12,M13,M23 – взаимоиндуктивности между контурами.
Первые три члена уравнения (2.23) определяют энергию независимых контуров, вторые три члена характеризуют энергию, обусловленную магнитной связью между контурами.
При расчёте силы, действующей между контурами, считается, что энергия меняется, только в результате возможного изменения взаимного расположения контуров. При этом энергия, обусловленная собственной индуктивностью, считается неизменной. Тогда сила, действующая на второй контур, равна:
![]() .
(2.24)
.
(2.24)
2.4.3 Усилия между параллельными проводниками
Если два параллельных
проводника обтекаются током и проводник
с током
![]() находится в магнитном поле тока
находится в магнитном поле тока
![]() ,
то величина усилия, действующего
между проводниками, согласно закону
Био-Савара Лапласа равна [2,3]:
,
то величина усилия, действующего
между проводниками, согласно закону
Био-Савара Лапласа равна [2,3]:
![]() ,
(2.25)
,
(2.25)
где
![]() - длина проводника, м;
- длина проводника, м;
![]() - расстояние между проводниками, м.
- расстояние между проводниками, м.
Направление электродинамических усилий зависит от направления токов и может быть определено по правилу левой руки. При одинаковом направлении токов проводники притягиваются друг к другу, а при противоположном - отталкиваются друг от друга.
Если размеры поперечного сечения проводников близки к расстоянию между проводниками, то, при определении электродинамических усилий между проводниками, необходимо учитывать размеры сечения проводников, так как в этом случае они оказывают существенное влияние на величину электродинамических усилий [3].
В
Рис. 2.7-Диагаграмма
для определения коэффициента формы
проводников прямоугольного сечения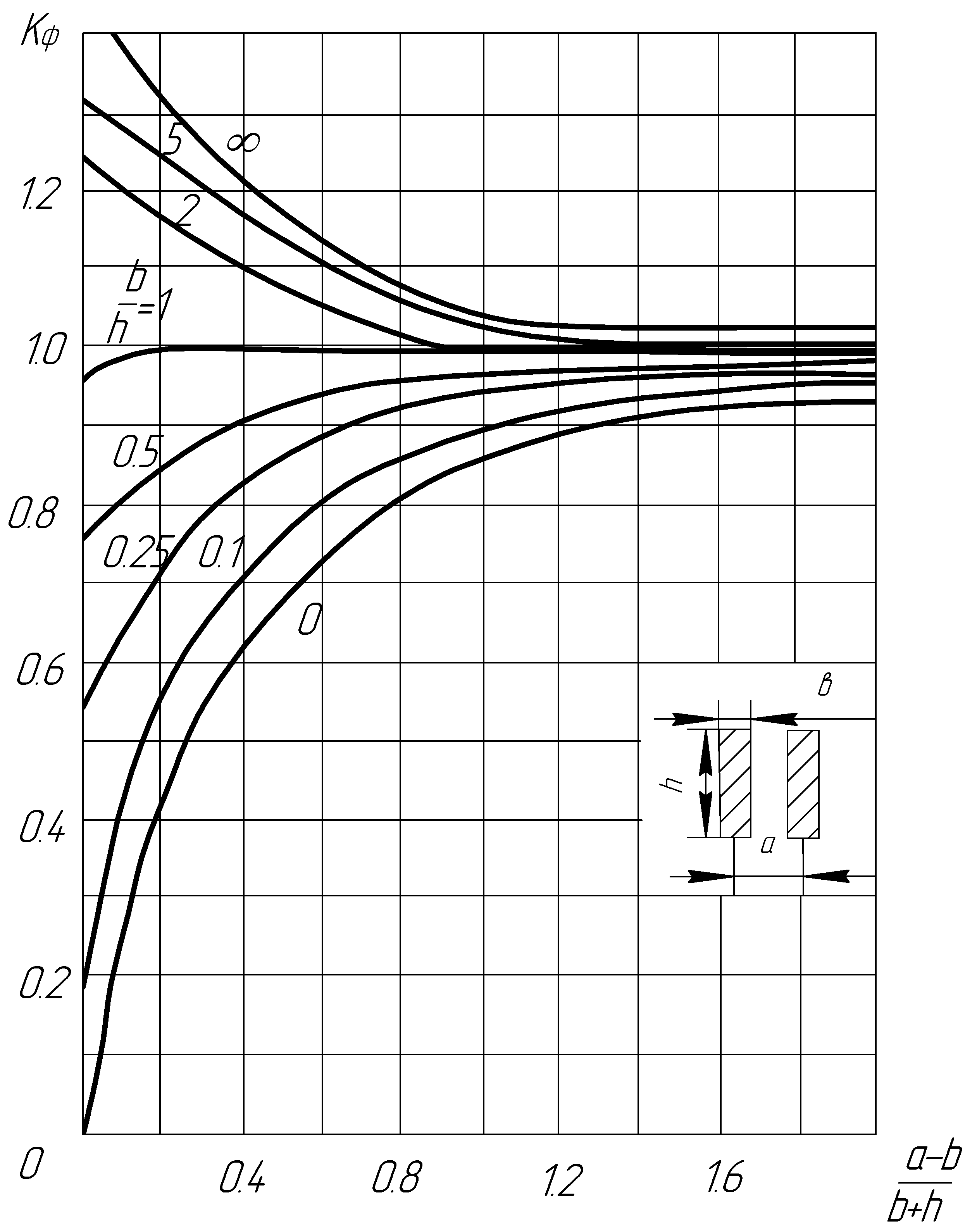
![]() .
С учётом коэффициента формы выражение
(2.25) имеет следующий вид:
.
С учётом коэффициента формы выражение
(2.25) имеет следующий вид:
![]() .
(2.26)
.
(2.26)
Диаграмма для определения коэффициента формы проводников прямоугольного сечения приведена на рис.а 2.7.
Если расстояние в свету между проводниками прямоугольной формы больше периметра поперечного сечения токоведущей части, т.е. a > 2 (b+h), то kф = 1. Для шин корытного сечения с высотой сечения h 0,1 м коэффициент формы шин kф = 1, при высоте h 0,6 м коэффициент формы kф = 1,1, а при высоте h 0,8 м коэффициент формы kф = 1,06. Для проводников кольцевого сечения и круглых проводников сплошного сечения коэффициент формы kф = 1.
