2.1.2. Напряженное состояние тела с трещиной

Практика эксплуатации реальных деталей показывает, что из-за концентрации напряжений, неточности сборки, влияния среды и т. п., стадия разрушения, состоящая из возникновения и развития трещины, начинается задолго до исчерпания несущей способности детали. При этом прочность материала детали не реализуется. В результате постепенного роста трещины длительность процесса разрушения от начала до полного разрушения занимает 90 % времени «жизни» детали и более. Вот почему практически инте­ресно не столько наличие трещины, сколько скорость ее роста в тех или иных условиях. В связи с этим основная задача механики разрушения — изучение прочности тел с трещинами, геометрии трещин, а также разработка критериев несущей способности элементов конструкций с трещинами.

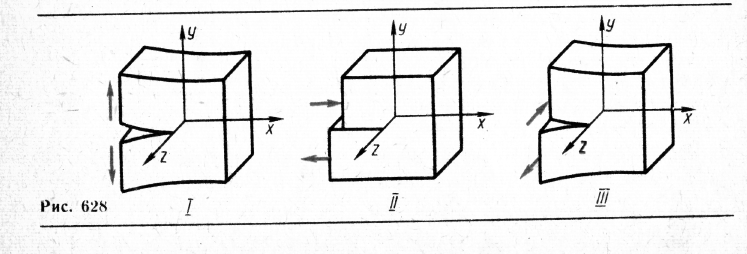
разрыв сдвиг срез

Рис.2.2. Типы растрескивания

В развитии трещины различают три простейших типа смещения ее берегов относительно друг друга в соответствии с действием различных внешних нагрузок (рис. 2.2). При деформации растяжения (схема I) возникает трещина отрыва, когда ее поверхности смещаются (расходятся) в направлениях, перпендикулярных к поверхности трещины; при деформации поперечного сдвига (схема II) поверхности берегов трещины смещаются поперек ее передней кромки; при нагрузке по схеме III образуются трещины продольного сдвига, при котором точки поверхности трещины смещаются вдоль ее передней кромки. Очевидно, если на тело с трещиной действует произвольная нагрузка в области применимости закона Гука, на основании принципа суперпозиции любое смещение берегов развивающейся трещины можно представить в виде суммы приведенных трех типов смещений.

Наиболее опасным и распространённым в технике является первый тип трещины, поэтому ограничимся рассмотрением напряжений в зоне вершины трещины именно этого типа.

Рассмотрим задачу о трещине типа I (рис. 2.3). На рисунке изображена бесконечная пластина, находящаяся под действием растягивающего напряжения σ, которое вызывается приложенными в бесконечности силами.

Рис.2.3. Трещина в бесконечной пластине

Нормальные напряжения, действующие на элементе dxdy, вычисляются следующим образом:

,

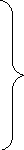(2.10)

,

,

σ_z = 0 (плоское напряженное состояние),

σ_z = ν (σ_x+ σ_y) (плоская деформация).

Для других типов трещин также получены выражения для напряжений, аналогичные формулам (2.10). Приведённое решение в силу его простоты является одним из основных в механике разрушения.

2.1.3. Коэффициенты интенсивности напряжений

Процесс разрушения материала сосредоточен в малой окрестности вершины трещины, где весьма высока концентрация напряжений, обусловленная малым радиусом закругления. Напряженное состояние в этой области при различных схемах нагружения на основе методов теории упругости формулы (2.10) можно в общем виде представить следующим образом:

, (2.11)

где i, j = x, у.

Величина К зависящая от вида нагружения, величины нагрузки и формы трещины, называется коэффициентом интенсивности напряжений (размерность К – сила/длина^3/2). В зависимости от вида нагрузки (см. схемы рис. 2.2) коэффициенты интенсивности напряжений отмечают соответственно индексами I, II или III, т. е. К_I, K_II, K_III, r и θ — полярные координаты с полюсом в вершине трещины; f_ij — некоторая функция угла θ.

Когда известен коэффициент К_I поле напряжений при вершине полностью определено. В частности, при плоском напряженном состоянии для нагрузки по схеме I формулы (2.10) имеют вид

,

, (2.12)

.

Перемещения u и v точек в направлении осей х и у соответственно определяются формулами

(2.13)

,

.

В случае плоской деформации, когда ε_z =0, в формулах (2.13) следует заменить (1–μ)/(1+μ) и 1/(1+μ) на величины (1–2μ) и (1–μ) соответственно.

Часто при расчетах бывает достаточно вместо рассмотрения самих напряжений оперировать только с коэффициентом К_I. Отсюда можно сделать вывод об использовании коэффициента интенсивности напряжений при построении критерия разрушения упругих тел с трещинами. Разработка методов отыскания значений этого коэффициента является важной проблемой в механике развития трещин.

По определению коэффициент интенсивности напряжений около вершины трещины при плоской деформации:

, (2.14)

что следует из анализа напряженного состояния у вершины трещины. Так, при растяжении пластины с трещиной длины 2l, расположенной посредине ширины пластины, этот анализ позволяет установить выражение для нормального напряжения в сечении пластины в окрестности трещины:

, (2.15)

где х – координата, отсчитываемая от середины трещины, r =х–l. У вершины трещины, при x→0,r→0, напряжения неограниченно возрастают по величине. Подставляя эти значения в (2.14) и вычисляя предел, находим:

. (2.16)

Аналогично можно получить выражения для коэффициентов интенсивности напряжений K_II и K_III соответственно схемам нагружения II и III на рис.2.2. Таким образом, имеем:

, , .

Коэффициент интенсивности напряжений не влияет на закон распределения напряжений, т. е. при одинаковых коэффициентах интенсивности напряжений в различных телах с трещинами, поля напряжений у вершин трещин будут одинаковыми. Это обстоятельство позволяет рассматривать коэффициент интенсивности напряжений К_I как параметр, характеризующий напряжённое состояние у вершины трещины в зависимости от формы тела, размеров трещины, способа нагружения.

Именно это обстоятельство и позволило принять величину К_I за критерий, определяющий начало роста трещины. По Д. Ирвину в линейной механике разрушения: трещина будет распространяться тогда, когда величина коэффициента интенсивности напряжений достигнет критического значения, характерного для данного материала.

Этот подход, получивший название силового, связан с представлениями о том, что разрушение обусловлено превышением напряжениями некоторого предельного значения. Принятие величины К_I за параметр, контролирующий рост трещины предполагает существование его предельного значения К_IС, соответствующего началу не­ко­н­т­рол­и­ру­е­мого роста трещины которое принимается за одну из характеристик материала.

Критерий развития трещин нормального отрыва имеет вид

К_I=K_Iс. (2.17)

Аналогично записывают два других критерия K_IIс и K_IIIс для трещин поперечного и продольного сдвига: К_II=K_IIс, К_III=K_IIIс

К_IС есть мера трещиностойкости материала. Поэтому К_IС называют «вязкостью разрушения при плоском деформированном состоянии». Для материалов с малой вязкостью разрушения допускаются только маленькие трещинки.

Критические значения коэффициентов интенсивности напряжений определяют экспериментально. Методика их определения регламентируется соответствующими стандартами.