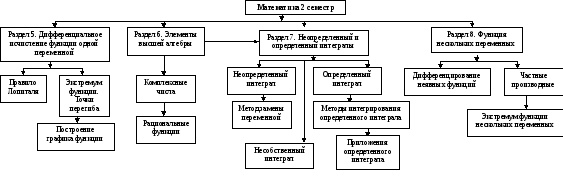
2.3. Структурно-логическая схема дисциплины «Математика»

2.4. Практический блок Практические занятия

№ темы	Наименование практических занятий	Кол-во часов по
		дневной форме обуч. (56 часов)	очно-заочной форме обуч. (36 часов)	заочной форме обуч. (20 часов)
Тема 1.2.	Решение систем линейных уравнений	4	4
Тема 1.3.	Матрицы и их применение к решению систем	2		2
Тема 3.3.	Уравнения плоскости и прямой в пространстве	4	4
Тема 3.4.	Кривые второго порядка	4	2	2
Тема 3.5.	Поверхности второго порядка	4		2
Тема 4.3.	Способы вычисления пределов	4	4	2
Тема 4.4.	Непрерывность функции. Точки разрыва	2		2
Тема 4.5.	Производная функции	4	4
Тема 5.1.	Правило Лопиталя	4	2	2
Тема 5.2.	Применение производной для исследования функции	4		2
Тема 7.1.	Первообразная. Неопределенный интеграл	4	4	2
Тема 7.3.	Определенный интеграл. Приложения	4	4
Тема 7.4.	Несобственный интеграл	4	4	2
Тема 8.1.	Функции нескольких переменных	4	2
Тема 8.2.	Экстремумы функций нескольких переменных	4	2	2

3. Информационные ресурсы дисциплины Библиографический список

Основной:

1. Лобунина, И.И. Линейная алгебра: учеб. пособие /И.И.Лобунина. - СПб.: изд-во СЗТУ, 2003, 2005.

2. Романова, Ю.С. Аналитическая геометрия: учеб. пособие /Ю.С.Романова. - СПб.: изд-во СЗТУ, 2007.

3. Пискунов, Н.С. Дифференциальное и интегральное исчисление. Т.1,2 /Н.С.Пискунов. - М.: 1985.

Дополнительный:

4. Шепелявая, Н.Б. Введение в математический анализ: учеб. пособие /Н.Б.Шепелявая. - СПб.: изд-во СЗТУ, 2005.

5. Волынская, И.А. Дифференциальное исчисление функций одной переменной: учеб. пособие /И.А.Волынская. - СПб.: изд-во СЗТУ, 2005.

6. Потапенко, А.А. Интегральное исчисление функций одной переменной: учеб. пособие /А.А.Потапенко. - СПб.: изд-во СЗТУ, 2005.

7. Гаврилов, В.Л. Дифференциальное исчисление функций нескольких переменных: учеб. пособие /В.Л.Гаврилов. - СПб.: изд-во СЗТУ, 2005.

8. Данко, Н.Е. Высшая математика в упражнениях и задачах. Т.1 /Н.Е. Данко, А.Г.Попов, Т.Я.Кожевникова. - М.: Высш. школа, 1980.

9. Задачи и упражнения по математическому анализу для втузов /под ред. Б.П.Демидовича. - М.: Наука, 1978.

10. Письменный, Д.Т. Конспект лекций по высшей математике. Ч.1 /Д.Т. Письменный – М.: Айрис-пресс, 2004.

4. Блок контроля освоения дисциплины

4.1. Методические указания по выполнению

контрольной работы N1

4.1.1. Определители и системы линейных уравнений

[1],Гл.1,§6

В различных разделах курса высшей математики используется понятие определителя. Определителем второго порядка называется число, обозначаемое символом и вычисляется по правилу:

.

Например,

Определитель третьего порядка будем вычислять, раскладывая его по элементам какой-либо строки или какого-либо столбца:

где I и k – целые числа от 1 до 3.

- алгебраические дополнения элементов -миноры элементов - определители второго порядка, получаемые вычеркиванием строки и столбца, на пересечении которых расположен элемент .

Пример 1. 1) Вычислить определитель , разложив его по элементам первой строки.

Решение:

2). Вычислить определитель , разложив его по элементам первого столбца.

Решение:

При решении систем п линейных уравнений с п неизвестными следует знать, что система имеет единственное решение в том и только в том случае, когда ее определитель не равен нулю. Решение системы уравнений в этом случае находят по формулам Крамера. Если же определитель системы равен нулю, система или несовместна, или имеет бесконечно много решений.

Пример 2. Решить систему уравнений

Решение: Вычисляем определитель системы – определитель, составленный из коэффициентов при неизвестных, разложив его, например, по элементам второго столбца.

Так как D 0, то система имеет единственное решение, определяемое по формулам Крамера:

(1)

Здесь D – определитель системы, - определители, получающиеся из определителя системы заменой столбца коэффициентов при соответствующем неизвестном столбцом свободных членов. Вычисляем .

Таким образом,

Проверим полученное решение, подставив значения

в систему уравнений

Все уравнения системы обратились в тождества, значит, система решена верно.