- •Математика, ч.1
- •1. Информация о дисциплине
- •1.1. Предисловие
- •1.2. Содержание дисциплины и виды учебной работы
- •2. Рабочие учебные материалы
- •2.1. Рабочая программа
- •Математика, I семестр
- •2.1.1. Основы линейной алгебры (25 часов) [1]
- •2.1.2. Основы векторной алгебры (8 часов) [1],[2]
- •2.1.3. Аналитическая геометрия (40 часов) [2]
- •2.1.4. Введение в математический анализ (62 часа) [3]
- •Математика, II семестр
- •2.1.5. Дифференциальное исчисление функций
- •2.1.6. Элементы высшей алгебры (14 часов) [3]
- •2.1.7. Неопределенный и определенный интегралы (38 часов) [3]
- •2.1.8. Функции нескольких переменных (32 часа) [3]
- •2.2. Тематический план дисциплины (1 курс)
- •2.2.1. Заочная форма обучения
- •2.2.2. Дневная форма обучения
- •2.2.3. Очно-заочная форма обучения
- •2.3. Структурно-логическая схема дисциплины «Математика»
- •2.4. Практический блок Практические занятия
- •3. Информационные ресурсы дисциплины Библиографический список
- •4.1.2. Матрицы и операции над ними
- •4.1.3. Векторы, операции над векторами. Скалярное, векторное, смешанное произведения векторов
- •Зная координаты перемножаемых векторов , можно вычислить скалярное произведение
- •4.1.4. Приложение векторной алгебры к задачам аналитической геометрии
- •4.1.5. Геометрические образы уравнений на плоскости и в пространстве
- •Вычисление пределов с использованием теорем
- •Бесконечно малые и бесконечно большие функции
- •Раскрытие неопределенностей
- •Вычисление пределов с использованием эквивалентных бесконечно малых величин
- •Непрерывность функции в точке и на промежутке. Точки разрыва функции
- •4.2.6. Производная и дифференциал
- •Вычисление производных
- •4.2.7. Дифференцирование сложной функции
- •4.2.8. Геометрический смысл производной и дифференциала функции
- •4.2.9. Дифференцирование функций, заданных параметрически
- •Следовательно, используя формулу (3), получаем
- •Применение правила Лопиталя к нахождению
- •4.3.2. Раскрытие неопределенностей типа и
- •4.3.3. Раскрытие неопределенностей типа
- •4.3.4. Применение производной к исследованию функции. Построение графиков функций
- •Промежутки монотонности и точки экстремума функции
- •4.3.5. Выпуклость и вогнутость графика функции. Точки перегиба
- •4.3.6. Асимптоты графика функции
- •4.3.7. Общий план исследования функции
- •Комплексные числа
- •Неопределенный интеграл
- •Основные свойства неопределенного интеграла
- •4.3.8. Метод замены переменной интегрирования (метод подстановки)
- •4.3.9. Метод интегрирования по частям
- •4.3.10. Интегрирование дробно-рациональных функций от различных выражений
- •Определенный интеграл
- •4.4.2. Несобственный интеграл от неограниченной функции
- •Геометрические приложения определенного интеграла
- •4.4.3. Вычисление площадей плоских фигур
- •4.4.4. Вычисление длин дуг кривых
- •4.4.5. Вычисление площадей поверхностей вращения
- •4.4.6. Вычисление объемов тел вращения
- •Дифференциальное исчисление функции нескольких переменных
- •Частные производные
- •Полный дифференциал
- •Наибольшее и наименьшее значения функции нескольких переменных в ограниченной области
- •4.5. Задания на контрольные работы nn 1-4
- •Задание на контрольную работу № 1
- •Задание на контрольную работу № 2
- •В задачах 71-80 найти первую производную функции
- •Задание на контрольную работу № 3
- •В задачах 131-140 найти неопределенные интегралы, используя для вычислений формулу интегрирования по частям.
- •Задание на контрольную работу № 4
- •4.6. Текущий контроль Тестовые задания
- •Содержание
Задание на контрольную работу № 1
В задачах 1-5 решить систему линейных уравнений по формулам Крамера.


В задачах 6-10 решить систему линейных уравнений с помощью обратной матрицы.


Задачи 11-20 решить средствами векторной алгебры.
11.
Найти площадь треугольника с вершинами
в точках
![]() .
.
12.
Найти объем треугольной пирамиды с
вершинами в точках
![]() и
и
![]() .
.
13.
Найти единичный вектор
![]() ,
перпендикулярный к векторам
,
перпендикулярный к векторам
![]() и
и
![]()
14.
При каком значение
![]() векторы
векторы
![]() будут компланарными?
будут компланарными?
15.
Найти проекцию вектора
![]() на направление вектора
на направление вектора
![]() перпендикулярного к векторам
перпендикулярного к векторам
![]() и
и
![]() .
.
16.
Найти острый угол между диагоналями
параллелограмма, построенного на
векторах
![]() и
и
![]()
17.
В треугольнике с вершинами в точке
![]() и
и
![]() проведена медиана
проведена медиана
![]() .
Найти вектор
.
Найти вектор
![]() параллельный медиане, длина которого
равна
параллельный медиане, длина которого
равна
![]()
18.
Найти угол между векторами
![]() и
и
![]() ,
если
,
если
![]()
![]() где
где
![]()
![]() и угол между векторами
и угол между векторами
![]() и
и
![]() равен
равен
![]()
19.
Векторы
![]() компланарны. Найти «m»
и
«n»
вектора
компланарны. Найти «m»
и
«n»
вектора
![]() если
если
![]() перпендикулярен
перпендикулярен
![]()
20.
Найти площадь параллелограмма,
построенного на векторах
![]() и
и
![]() если
если
![]()
![]() и угол между векторами
и угол между векторами
![]() и
и
![]() равен
равен
![]() .
.
Задачи 21-30 решить методами аналитической геометрии.
21.
Найти уравнение плоскости, проходящей
через точки
![]() и
и
![]() перпендикулярно плоскости
перпендикулярно плоскости
![]() .
.
22.
Найти точку пересечения с осью
![]() плоскости, проходящей через три точки
плоскости, проходящей через три точки
![]() и
и
![]()
23.
Найти уравнение плоскости, проходящей
через точку
![]() перпендикулярно плоскостям
перпендикулярно плоскостям
![]() и
и
![]()
24.
Найти уравнение плоскости, проходящей
через начало координат и точку
![]() параллельно прямой, проходящей через
точки
параллельно прямой, проходящей через
точки
![]()
25.
Найти уравнение плоскости, проходящей
через прямую
 параллельно прямой
параллельно прямой

26.
Найти канонические уравнения прямой,
проходящей через точку
![]() и точку пересечения прямой
и точку пересечения прямой
 с плоскостью
с плоскостью
![]()
27.
Найти проекцию начала координат на
плоскость, проходящую через точки
![]() и
и
![]()
28.
Найти параметрические уравнения прямой,
проходящей через точку
![]() параллельно прямой
параллельно прямой
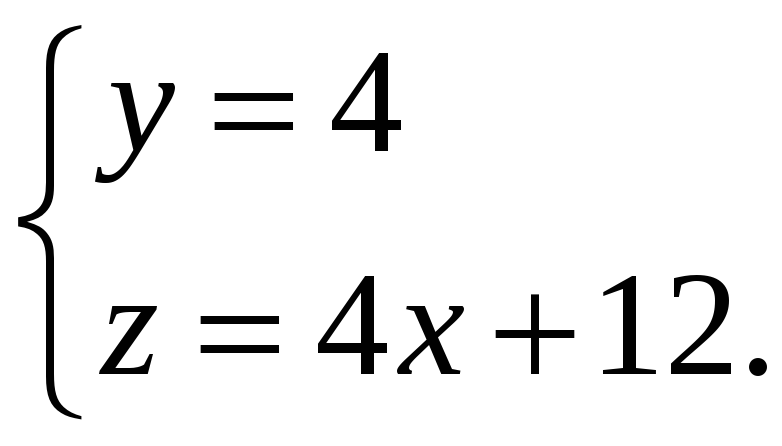
29.
Найти проекцию точки
![]() на прямую
на прямую
 .
.
30.
Дан треугольник с вершинами
![]() Написать уравнение плоскости, проходящей
через сторону AB
перпендикулярно
плоскости заданного треугольника.
Написать уравнение плоскости, проходящей
через сторону AB
перпендикулярно
плоскости заданного треугольника.
В задачах 31-40 найти координаты точек пересечения кривых. Указать вид кривых. Сделать чертеж.

В задачах 41-50 сделать схематический рисунок тела, заданного системой неравенств. Указать вид поверхностей, ограничивающих это тело. Определить, по каким линиям и в каких плоскостях пересекаются эти поверхности.

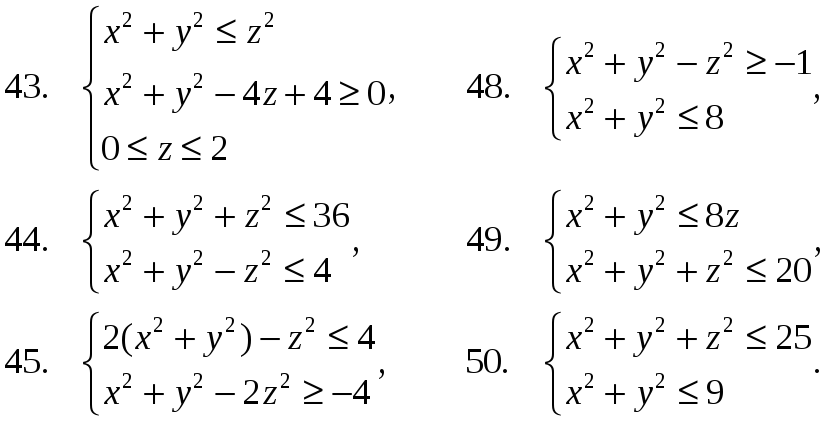
Задание на контрольную работу № 2
В задачах 51-60 найти пределы функций, используя эквивалентные бесконечно малые величины и тождественные преобразования.
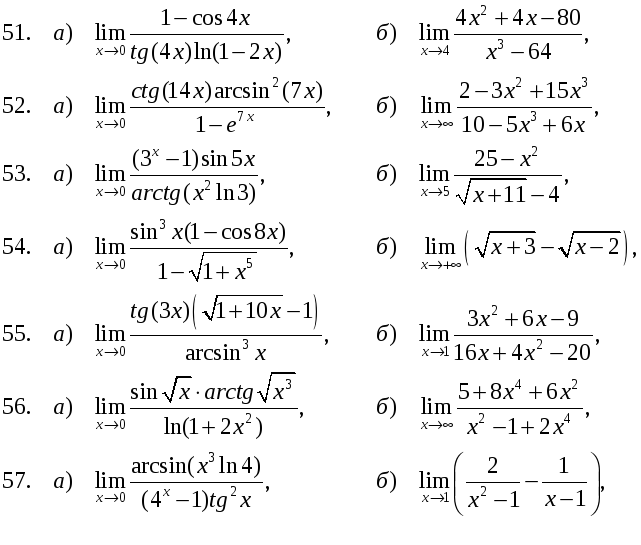

В задачах 61-70 а) найти точки разрыва функций, если они существуют; б) найти односторонние пределы в точках разрыва и установить тип точек разрыва; в) сделать схематический чертеж графика функции в окрестности точек разрыва.

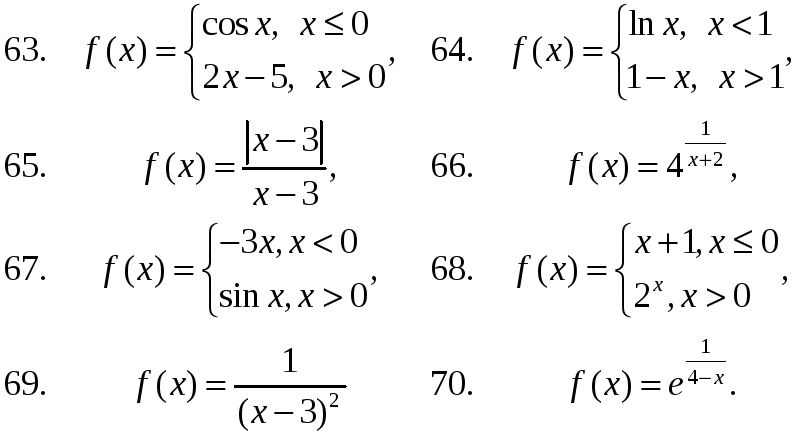
В задачах 71-80 найти первую производную функции
![]() ,
,
 ,
,
![]() ,
,
 ,
,
![]() ,
,
![]() ,
,
 ,
,
![]() ,
,
 ,
,
![]() ,
,
В
задачах 81-85 найти координаты точки
пересечения с осью
![]() касательной, проведенной к графику
функции
касательной, проведенной к графику
функции
![]() в заданной точке. Сделать чертеж.
в заданной точке. Сделать чертеж.

![]()
В
задачах 86-90 найти координаты точки
пересечения с осью
![]() касательной, проведенной к графику
функции
касательной, проведенной к графику
функции
![]() в заданной точке. Сделать чертеж.
в заданной точке. Сделать чертеж.

![]()
В
задачах 91-100 найти
![]() и
и
![]() функции, заданной параметрически
функции, заданной параметрически