
- •Математика, ч.1
- •1. Информация о дисциплине
- •1.1. Предисловие
- •1.2. Содержание дисциплины и виды учебной работы
- •2. Рабочие учебные материалы
- •2.1. Рабочая программа
- •Математика, I семестр
- •2.1.1. Основы линейной алгебры (25 часов) [1]
- •2.1.2. Основы векторной алгебры (8 часов) [1],[2]
- •2.1.3. Аналитическая геометрия (40 часов) [2]
- •2.1.4. Введение в математический анализ (62 часа) [3]
- •Математика, II семестр
- •2.1.5. Дифференциальное исчисление функций
- •2.1.6. Элементы высшей алгебры (14 часов) [3]
- •2.1.7. Неопределенный и определенный интегралы (38 часов) [3]
- •2.1.8. Функции нескольких переменных (32 часа) [3]
- •2.2. Тематический план дисциплины (1 курс)
- •2.2.1. Заочная форма обучения
- •2.2.2. Дневная форма обучения
- •2.2.3. Очно-заочная форма обучения
- •2.3. Структурно-логическая схема дисциплины «Математика»
- •2.4. Практический блок Практические занятия
- •3. Информационные ресурсы дисциплины Библиографический список
- •4.1.2. Матрицы и операции над ними
- •4.1.3. Векторы, операции над векторами. Скалярное, векторное, смешанное произведения векторов
- •Зная координаты перемножаемых векторов , можно вычислить скалярное произведение
- •4.1.4. Приложение векторной алгебры к задачам аналитической геометрии
- •4.1.5. Геометрические образы уравнений на плоскости и в пространстве
- •Вычисление пределов с использованием теорем
- •Бесконечно малые и бесконечно большие функции
- •Раскрытие неопределенностей
- •Вычисление пределов с использованием эквивалентных бесконечно малых величин
- •Непрерывность функции в точке и на промежутке. Точки разрыва функции
- •4.2.6. Производная и дифференциал
- •Вычисление производных
- •4.2.7. Дифференцирование сложной функции
- •4.2.8. Геометрический смысл производной и дифференциала функции
- •4.2.9. Дифференцирование функций, заданных параметрически
- •Следовательно, используя формулу (3), получаем
- •Применение правила Лопиталя к нахождению
- •4.3.2. Раскрытие неопределенностей типа и
- •4.3.3. Раскрытие неопределенностей типа
- •4.3.4. Применение производной к исследованию функции. Построение графиков функций
- •Промежутки монотонности и точки экстремума функции
- •4.3.5. Выпуклость и вогнутость графика функции. Точки перегиба
- •4.3.6. Асимптоты графика функции
- •4.3.7. Общий план исследования функции
- •Комплексные числа
- •Неопределенный интеграл
- •Основные свойства неопределенного интеграла
- •4.3.8. Метод замены переменной интегрирования (метод подстановки)
- •4.3.9. Метод интегрирования по частям
- •4.3.10. Интегрирование дробно-рациональных функций от различных выражений
- •Определенный интеграл
- •4.4.2. Несобственный интеграл от неограниченной функции
- •Геометрические приложения определенного интеграла
- •4.4.3. Вычисление площадей плоских фигур
- •4.4.4. Вычисление длин дуг кривых
- •4.4.5. Вычисление площадей поверхностей вращения
- •4.4.6. Вычисление объемов тел вращения
- •Дифференциальное исчисление функции нескольких переменных
- •Частные производные
- •Полный дифференциал
- •Наибольшее и наименьшее значения функции нескольких переменных в ограниченной области
- •4.5. Задания на контрольные работы nn 1-4
- •Задание на контрольную работу № 1
- •Задание на контрольную работу № 2
- •В задачах 71-80 найти первую производную функции
- •Задание на контрольную работу № 3
- •В задачах 131-140 найти неопределенные интегралы, используя для вычислений формулу интегрирования по частям.
- •Задание на контрольную работу № 4
- •4.6. Текущий контроль Тестовые задания
- •Содержание
4.2.6. Производная и дифференциал
[4],§4; [3],т.1,гл.3,§§2-16; [8],гл.7,§1; [9],гл.2,§§1-6
Вычисление производных
Основные правила дифференцирования:
Если функция и(х) и v(x) дифференцируемы в точке х, то в этой точке:

Таблица производных:

Пример
21. Найти
производную функции

Решение: Используем первое и второе правила дифференцирования
![]()

Далее используем формулу для нахождения производной степенной функции (табличная формула N 2):

Пример
22. Найти
производную функции
![]()
Решение: Используем правило дифференцирования произведения и табличные формулы N 4 и N 11:

Пример
23. Найти
производную функции

Решение: Используем правило дифференцирования частного и табличные формулы N 9 и N 13:

4.2.7. Дифференцирование сложной функции
Производная сложной функции у = f(u(x)) вычисляется по формуле
![]()
То есть, чтобы найти производную сложной функции, нужно сначала продифференцировать "внешнюю" функцию по промежуточному аргументу и так, как если бы аргумент и был независимой переменной, после чего умножить полученный результат на производную от функции и по переменной х.
Это правило распространяется на сложную функцию, состоящую из любого конечного числа дифференцируемых функций.
Пример
24. Найти
производную функции
![]()
Решение:
Данная
функция - сложная, промежуточный аргумент
![]() .
Согласно приведенному правилу имеем
.
Согласно приведенному правилу имеем

Пример
25.
Найти производную функции
![]()
Решение:
Данная
сложная функция составлена из трех
функций
![]() где
где
![]() Применяем правило
дифференцирования сложной функции
(начиная дифференцировать
с "внешней" функции f
):
Применяем правило
дифференцирования сложной функции
(начиная дифференцировать
с "внешней" функции f
):


4.2.8. Геометрический смысл производной и дифференциала функции
П усть
в декартовой прямоугольной системе
координат задана кривая,
являющаяся графиком функции
усть
в декартовой прямоугольной системе
координат задана кривая,
являющаяся графиком функции
![]() и
на ней точка
и
на ней точка
![]() Производная
Производная
![]() функции
функции
![]() геометрически
представляет собой
угловой
коэффициент касательной к графику
функции в точке с абсциссой
геометрически
представляет собой
угловой
коэффициент касательной к графику
функции в точке с абсциссой
![]() ,
т.е.
,
т.е.
![]() (см.
рис.12). Тогда уравнение
касательной
к кривой
(см.
рис.12). Тогда уравнение
касательной
к кривой
![]() в
точке
в
точке
![]() имеет
вид:
имеет
вид:
![]()
Дифференциал
функции f(x)
в
точке
![]() находится по формуле
находится по формуле
![]() ,
т.е. равен произведению производной
функции в
заданной точке на дифференциал(приращение)
независимой переменной. Геометрически
дифференциал функции
,
т.е. равен произведению производной
функции в
заданной точке на дифференциал(приращение)
независимой переменной. Геометрически
дифференциал функции
![]() в точке
в точке
![]() представляет
собой приращение
ординаты касательной к
графику функции в
точке
представляет
собой приращение
ординаты касательной к
графику функции в
точке
![]() и при
и при
![]() являются
эквивалентными бесконечно малыми.
Поэтому справедливо приближенное
равенство
являются
эквивалентными бесконечно малыми.
Поэтому справедливо приближенное
равенство
![]() ~
dy,
позволяющее
приближенно заменять приращение функции
дифференциалом.
~
dy,
позволяющее
приближенно заменять приращение функции
дифференциалом.
Пример
26. Найти
координаты точки пересечения с осью Оу
касательной
к кривой
![]() ,
где
,
где
 ,
проведенной к ней в точке
,
проведенной к ней в точке
![]()
Решение:
Уравнение
касательной к кривой
![]() в точке
в точке
![]() имеет
вид
имеет
вид
![]() .
Найдем
сначала производную
.
Найдем
сначала производную
![]() :
:

Вычислим
 тогда уравнение касательной к заданной
кривой в точке Мо(-1,4)
запишется в виде:
тогда уравнение касательной к заданной
кривой в точке Мо(-1,4)
запишется в виде:
![]()
Теперь находим координаты точки пересечения полученной прямой с осью Оу.
Для
всех точек, лежащих на оси
![]() ,
,
![]() .
Подставим в уравнение касательной
.
Подставим в уравнение касательной
![]() ,
получим
,
получим
![]() .
Значит, касательная
.
Значит, касательная
![]() пересекает ось
пересекает ось
![]() в
точке (0,8).
в
точке (0,8).
4.2.9. Дифференцирование функций, заданных параметрически
Производная
функции
![]() ,
заданной
в параметрической форме:
,
заданной
в параметрической форме:
![]()
![]() ,
находится
по формуле
,
находится
по формуле
 (2)
(2)
Пример
27. Найти
производные
![]() и
и
![]() функции
функции
![]()
заданной
в параметрической форме

Решение:
Вычислим
![]() и
и
![]() :
:


Используя формулу (2), получим
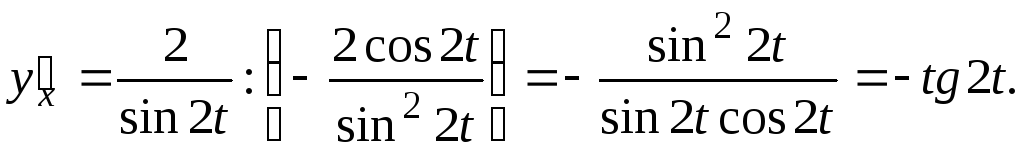
Итак,
 Так как
Так как
 ,
то для нахождения
,
то для нахождения
![]() можно использовать ту же формулу
дифференцирования функции, заданной
параметрически, применив ее к функции
можно использовать ту же формулу
дифференцирования функции, заданной
параметрически, применив ее к функции
![]() ,
то есть:
,
то есть:
 (3)
(3)
Вычислим
 :
:

