1. Вычисление пределов с использованием теорем

о конечных пределах

Справедливы следующие теоремы:

1. , (С - постоянная)

2. 

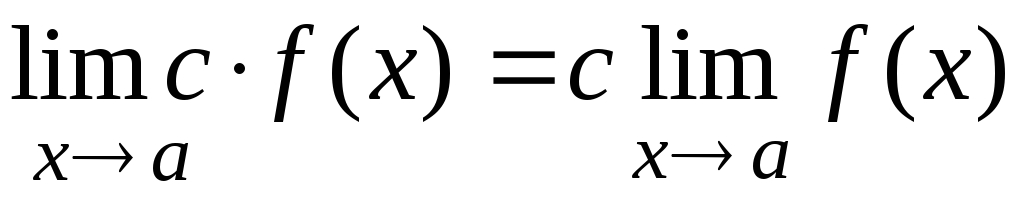
3. Если каждая из функций f(х) и g(х) имеет при конечный предел, то

Для нахождения предела элементарной функции f(х) при х→a в случае, если а - конечная точка, принадлежащая области определения f(х), нужно вычислить значение этой функции при х = а. Это значение и будет искомым пределом, т.е.

Пример 10. Найти пределы функций при

а)

б)

в)

Решение: Данные функции элементарные, поэтому можно применить сформулированное правило:

а)

б)

в)

2. Бесконечно малые и бесконечно большие функции

Функция называется бесконечно малой в точке а (или при ), если функция называется бесконечно большой в точке а (или при ), если

Справедливы теоремы:

1. Сумма конечного числа бесконечно малых в точке a функций -бесконечно малая функция.

2. Если f(x) - функция, ограниченная в некоторой окрестности точки а, функция g(х) - бесконечно малая в этой точке, то функция f(x) ∙ g(х) - бесконечно малая.

3. Если при функция стремится к отличному от нуля пределу, а функция - бесконечно большая при , то функция f(x) ∙ g(х) - бесконечно большая при .

4. Если функция - бесконечно малая в точке и в некоторой окрестности этой точки не равна нулю, то функция - бесконечно большая в точке а; если - бесконечно большая в точке а, то - бесконечно малая.

Пример 11. Найти a) ; б) .

Решение:

а) При функция (х - 1) - бесконечно малая, значит, - бесконечно большая, следовательно, - бесконечно большая, т.е.

б) При функция -бесконечно большая, поэтому - бесконечно малая. Функция - ограниченная, значит, произведение - бесконечно малая, т.е.

3. Раскрытие неопределенностей

Если при формальной подстановке предельного значения аргумента получается выражение вида

то для нахождения пределов функций необходимо проводить преобразования данных выражений.

Пример 12. Найти

Решение: Непосредственная подстановка значения приводит к неопределенности вида . Разложим на множители числитель и знаменатель дроби, выделим общий множитель и сократим на него дробь.

Для разложения числителя воспользуемся формулой:

.

В знаменателе дроби стоит квадратный трехчлен. Если квадратный трехчлен имеет корни , то он раскладывается на множители следующим образом:.

Данный квадратный трехчлен имеет корни поэтому Таким образом,

Пример 13. Найти

Решение: Непосредственно подставляя х = 0, получаем неопределенность . Умножим и разделим данную дробь на выражение, сопряженное числителю, то есть на

Замечание: Если в примере иррациональность имеется в числителе и знаменателе дроби, то дробь следует умножить и разделить на выражение, сопряженное числителю и на выражение, сопряженное знаменателю.

Пример 14. Найти

Решение: В этом примере неопределенность вида Вынесем за скобки в числителе х³, а в знаменателе х² (наивысшую степень х для каждого многочлена):

Величины 1/х, 1/х²,1/х³, обратные бесконечно большим,- бесконечно малые, и, значит, выражение в скобках стремится к 3/7. х - бесконечно большая величина, следовательно, произведение х ∙ 3/7 также величина бесконечно большая, то есть

Аналогичный прием вычисления пределов можно использовать для раскрытия неопределенностей в случае иррациональных функций.

Пример 15. Найти .

Решение:

Так как , то x>0 и, значит, |x| = x. Поэтому

Пример 16. Найти .

Решение: Имеем неопределенность вида (). Умножим и разделим данное выражение на сопряженное:

Получим неопределенность вида Раскроем ее стандартным способом:

Так как , то x<0 и, значит, |x| = -x. Тогда