Тема: Векторное и смешанное умножение векторов.

Вариант 1. Вариант 2.

1. Две силы и приложены к точкам и соответственно. Определить суммарный момент этих сил относительно точки h .

; ;

2. Вычислить площадь треугольника, две стороны которого совпадают с векторами , , если и

; ;

3. Вектор перпендикулярен векторам и и образует острый угол с осью OZ . Найти координаты вектора , если его длина равна 3 и

; ;

; ;

4. Найти вектор , зная, что он перпендикулярен векторам и и удовлетворяет условию

; ;

5. Объем тетраэдра, у которого три ребра, выходящие из одной вершины, совпадают с векторами , равен V. Определить объем тетраэдра, построенного аналогичным образом на векторах

; ;

6. Объем тетраэдра V = 5 , а три его вершины находятся в точках , , . Найти координаты четвертой вершины, если известно, что она лежит на оси

OZ; OY;

АИГ=П/З № 10 ОТВЕТЫ ОС___________

Тема: Векторное и смешанное умножение векторов.

Вариант 1. Вариант 2.

01. 01.

02. 02.

03. ; 03. ;

04. ; 04. ;

05. ; 05. ;

06. 06.

АИГ=П/З № 12 ЗАДАНИЕ ОС___________

Тема: Декартовы системы координат. Площадь треугольника. Центр масс.

Вариант 1. Вариант 2.

1. Треугольник ABC задан координатами своих вершин. Доказать, что он прямоугольный, если

2. На оси ординат найти точку, отстоящую от точки A на расстоянии 13 единиц, если

, .

3. Вершина A треугольника ABC лежит на оси абсцисс. Может ли угол при вершине A быть прямым, если

4. Треугольник ABC задан координатами своих вершин. Определить координаты точки M , с которой совпадает вершина A, если перегнуть чертеж по прямой BC .

5. Найти площадь треугольника, заданного координатами своих вершин :

6. Две вершины треугольника расположены в точках и . Найти

координаты третьей вершины, расположенной на оси OX, если площадь треугольника равна

S = 5 кв. ед., S = 3 кв. ед.

7. Определить положение центра масс соприкасающихся однородных колец с радиусами R и r , если касание

внешнее внутреннее

8. Концы однородного стержня расположены на разных осях координат. Найти длину стержня, если его центр масс расположен в точке

. .

АИГ=П/З № 12 ОТВЕТЫ ОС___________

Тема: Декартовы системы координат. Площадь треугольника. Центр масс.

Вариант 1. Вариант 2.

01. Прямой угол при вершине “B” 01. Прямой угол при вершине “A”

02. 02.

03. Прямой угол при вершине A 03. Прямой угол при вершине A

когда ее абсцисса равна когда ее абсцисса равна

04. Использовать равенства 04. Использовать равенства

05. S = 10 кв.ед. 05. S = 3 кв.ед.

06. 06.

07. 07. .

08. 08.

АИГ=П/З № 13 ЗАДАНИЕ ОС - _______

Тема: Составление уравнений геометрических мест точек.

Вариант 1. Вариант 2.

1. Два стержня вращаются вокруг двух неподвижных точек A и B. При этом вращении стержни остаются все время перпендикулярными друг к другу. Найти геометрическое место точек пересечения стержней, если

2. Найти геометрическое место точек равноудаленных от оси OX и от точки P, если

; ;

3. Найти геометрическое место точек равноудаленных от начала координат и окружности

. .

4. Найти геометрическое место точек равноудаленных от двух данных окружностей:

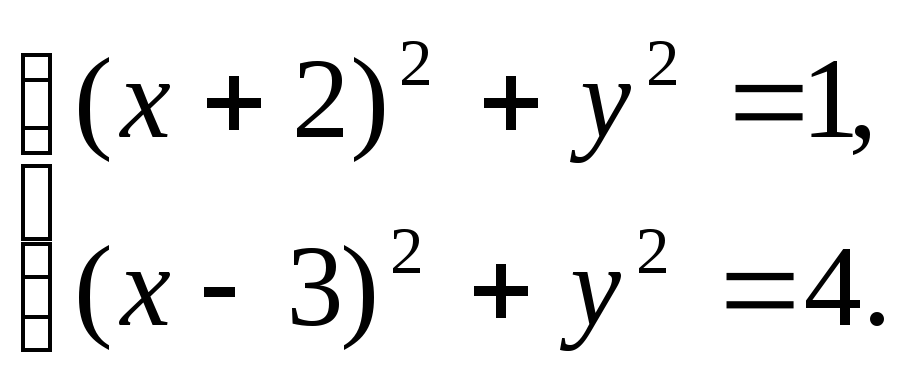
5. Найти геометрическое место центров окружностей, касающихся двух данных окружностей:

6. Составить уравнение кривой ( овал Кассини ), определяемой как геометрическое место точек, произведение расстояний которых от двух данных точек P и Q есть величина постоянная, равная , если

7. Отрезок прямой AB, длина которого равна 4 ед. , скользит своими концами по координатным осям. Точка M делит отрезок на две части. Найти траекторию точки M, если

, .

АИГ=П/З № 13 ОТВЕТЫ ОС_______