Сосредоточенной силой и моментом
Дано
=2
м,
=12
кН/м, отношения
=0,8;
=0,6;
форма сечения − коробчатое сечение
при соотношении всех сторон 2 (рис. 6.1,
а,
в).
1. Построение эпюр продольных сил, поперечных сил и изгибающих моментов
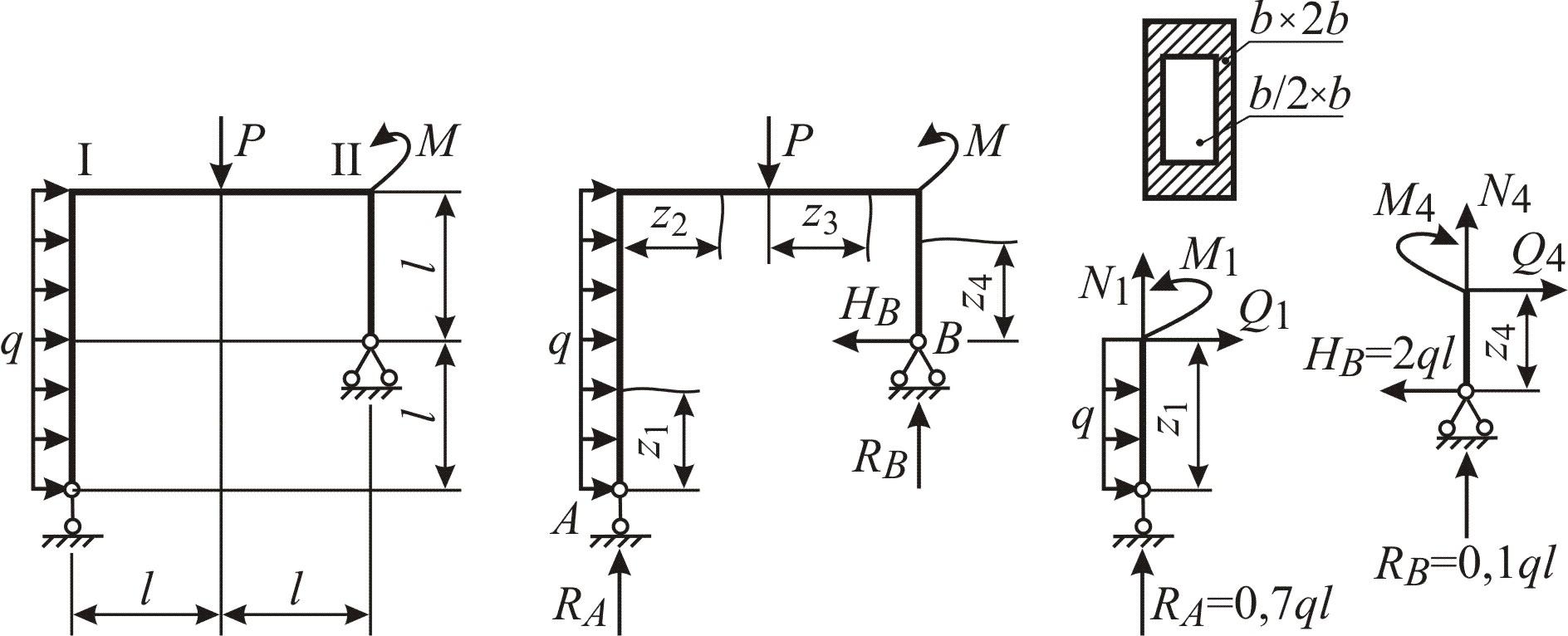
Определим опорные реакции, составив уравнения (6.1).
Получаем
Проверим реакции неиспользованным уравнением ∑ пр y≡ 0:
,
,
.
Построим эпюры
продольных сил
,
поперечных сил Q
и изгибающих моментов M.
Разделяем раму на грузовые участки. В
рамах границами участков являются также
и узлы. Поэтому имеем четыре силовых
участка. Абсциссы z
текущих сечений для всех участков
показаны на рис. 6, б.
Правила знаков продольных
сил N
при растяжении-сжатии и эпюр поперечных
сил
Q
и изгибающих моментов
M
такие, как
при
растяжении-сжатии и при плоском изгибе
балок.
Рассматривая равновесие отсечённой части, наблюдатель находится внутри рамы лицом к стержню.
|
|
|
||
|
а |
б |
||
|
|
|
|
|
|
в |
г |
||
Рис 6.1
1-й участок: 0 ≤ z1 ≥ 2l. Составляя уравнения (6.2) для отсечённой части 1-го участка, изображённой на рис. 6, г, получаем
− сжатые волокна
справа;
2-й участок: 0 ≤ z2 ≥ , (см. рис. 6, б):
– сжатые волокна
снизу;
3-й участок: 0 ≤ z3 ≥ l, (см. рис. 6, б):
–
− сжатые волокна снизу.
|
|
|
а |
|
|
|
б в |
|
|
|
г д |
Рис 6.2
4-й участок: 0 ≤ z4 ≥ l. Начало координаты z4 для удобства выбираем в опоре В, для отсечённой части 4-го участка, изображённой на рис. 6, г, получаем
– сжатые волокна
справа.
Откладывая полученные значения на схемах рамы, строим эпюры N, Q, M (рис. 6.2, а, б). Положительные значения ординат сил будем откладывать снаружи рамы, отрицательные – внутри. Эпюры изгибающих моментов строим на сжатых волокнах.
На 1-м участке эпюра N представляет собой прямоугольник с положительной ординатой N = –0,7qa. Её откладываем справа от оси первого участка. Эпюра Q ограничена наклонной линией, проходящей через начало координат. Все ординаты отрицательные, откладываем их справа от оси рамы. Выражение М – квадратная парабола, так как на эпюре Q наклонная линия не пересекает ость стержня, то на эпюре М – кривая без перегиба. Строим эпюру М справа от оси первого участка.
На 2-м участке имеем отрицательные постоянные значения N и Q, – на эпюрах откладываем значения вниз от оси рамы и строим прямоугольники; эпюра М ограничена наклонной прямой.
На 3-м и 4-м участках характер эпюр сохраняется таким же, как и на втором участке. В точке приложения силы Р на эпюре Q имеется скачок, на эпюре М – излом навстречу силе.
Правила контроля эпюр Q и М в рамах те же, что для балок (см. Приложение). К обычным правилам контроля для балок добавляется еще одно: все узлы рамы должны находиться в равновесии под действием сил и изгибающих моментов. Используем это правило. Двумя бесконечно близкими сечениями вырежем узел I (рис. 6.1, а) и приложим в этих сечениях соответствующие внутренние усилия, значения которых берём из эпюр N, Q, M (см.рис. 6.3, а).
Составляем уравнения статики (6.2)
∑ пр z = 0; ∑ пр y= 0, ∑ мом (уз I) = 0:
Убеждаемся, что узел I находится в равновесии. Аналогично проверяем равновесие узла II (рис. 6.3, б).
|
|
|
|
а |
б |
Рис. 6.3