1. Выборочная линейная среднеквадратическая регрессия

Линейная регрессия является простейшей регрессионной моделью, согласно которой функция регрессии является линейной 2-параметрической функцией:

,

где - неопределенные коэффициенты, которые оценим по наблюдаемым данным. Пусть имеется двухфакторная выборка n наблюдений за величинами X и Y, которую будем называть корреляционным полем. Помимо выборочных средних значений и выборочных дисперсий , вычислим так же среднее произведение и выборочный (эмпирический) коэффициент корреляции , который является выборочным аналогом теоретического коэффициента корреляции Пирсона .

Построим оценки коэффициентов методом наименьших квадратов. Для этого найдем такие значения , которые минимизируют сумму квадратов отклонения и , то есть ошибки

.

Из необходимых условий минимума найдем искомые оценки :

; ; ,

; ; .

Через выборочный коэффициент корреляции , коэффициент представим в форме , а уравнение выборочной линейной среднеквадратической регрессии имеет одну из следующих форм:

; ;

; .

2. Свойства линейной регрессии и коэффициента корреляции.

Построенная выборочная линейная среднеквадратичная регрессия является простейшим приближение корреляционной зависимости, показывает тенденцию (тренд) этой зависимости и изображается прямой на корреляционном поле, наименее уклоняющейся от его точек. Прямая линия регрессии проходит через точку , отсекает от оси отрезок , и имеет угол наклона с тангенсом равным как это изображено на рис. 15.1.

Рис. 15.1 Прямая линейной среднеквадратической регрессии.

Выборочный коэффициент корреляции характеризует степень корреляционной зависимости наблюдаемых величин Х и У и обладает следующими свойствами:

1. ,

2. для независимых Х и У коэффициент близок к нулю,

3. для линейно зависимых величин он близок к единице.

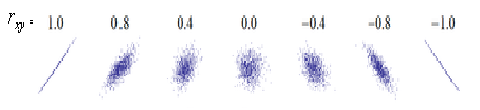
Геометрически он показывает «тесноту» корреляционного поля возле прямой линии регрессии, что иллюстрирует следующий рисунок для различных значений коэффициента:

.

Рис. 15.2 Корреляционное поле для различных уровней корреляции величин

На рис. 15.2 видно, что некоррелированной выборке соответствует неориентированное шаровое корреляционное поле, с ростом поле сжимается и ориентируется к прямой. Знак коэффициента говорит о нарастающем или убывающем тренде зависимости.

Ошибки регрессии имеют нулевое среднее значение , так как , и минимальную в соответствии с методом наименьших квадратов дисперсию , так называемую остаточную дисперсию, которая тем меньше, чем выше коэффициент корреляции. Величина выборочной дисперсии является статистической оценкой для дисперсии ошибки , однако, это смещенная оценка. Несмещенной (исправленной) оценкой является величина , величина называется стандартной ошибкой регрессии. Ошибки для коэффициентов регрессии вычисляются по формулам:

, .

В корреляционном анализе также вводится понятие коэффициента детерминации , показывающего долю объясненной части дисперсии объясняемой переменной Y. Поскольку , то коэффициент детерминации представим так же в следующем виде

,

показывающем его прямую связь с коэффициентом корреляции.

Известно [9] распределение случайных величин, связанных с введенными выше коэффициентами при условии независимости величин и :

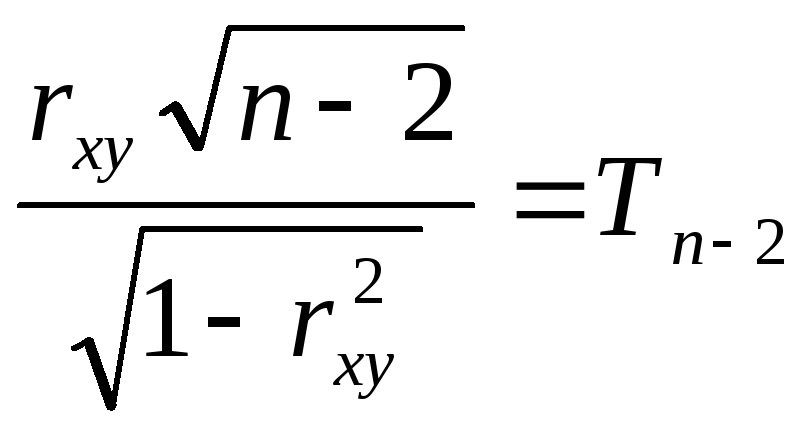~ распределение Стьюдента с степенями свободы,

~ F-распределение Фишера с степенями свободы.

Эти величины используется для построения критериев значимости выборочных коэффициентов и , и их распределение приводится приложениях 3 и 5 соответственно. Действительно, например, задаваясь уровнем значимости проверяемой гипотезы , соответствующей независимости величин Х и Y, можно сравнить наблюдаемое значение критерия , с критическим значением . Если , то гипотеза принимается, что говорит о не значимости выборочного коэффициента корреляции мало отличного от нуля. Если же , то гипотеза отвергается, то есть выборочный коэффициент корреляции, а значит и уравнение регрессии, значимы. Значимость коэффициента корреляции говорит о том, что полученный по данной выборке коэффициент неслучайно отличен от нуля, а корреляционная зависимость между наблюдаемыми величинами существенна.

Аналогично строится критерий Фищера для проверки гипотезы о значимости коэффициента детерминации :

, гипотеза принимается, т.е. незначим.

Выводы этих критериев значимости и идентичны [9].

Значимость коэффициентов регрессии может быть оценена по уровню значимости по критериям Стьюдента

, .