
- •1. Элементы комбинаторики и вычисление вероятности событий
- •2. Геометрические вероятности
- •1. Определение условной вероятности
- •2. Независимость событий
- •3. Вероятность произведения событий
- •4. Теорема сложения вероятностей событий
- •5. Формула полной вероятности
- •6. Формула Байеса
- •1. Формула Бернулли
- •2. Полиноминальная формула Бернулли
- •3. Теоремы Муавра-Лапласа
- •4. О границах применимости схемы Бернулли
4. О границах применимости схемы Бернулли
Схема повторных испытаний Бернулли в силу своей простоты и наглядности имеет большое распространение не только в учебном процессе, но и практических приложениях. Однако надо помнить, что в ее основе лежат три основополагающих принципа:
- однородность (одинаковость, повторяемость) испытаний,
- независимость испытаний между собой,
- стационарность испытания (постоянство вероятностей его исходов).
_______________
Пример.
На складе находится
![]() деталей, причем из них
деталей, причем из них
![]() бракованных.
Рабочий взял наудачу
бракованных.
Рабочий взял наудачу
![]() деталей, какова вероятность того, что
у него окажется
деталей, какова вероятность того, что
у него окажется
![]() бракованных
деталей.
бракованных
деталей.
Решение.
Часто
студенты, не владеющие полностью
материалом курса, начинают рассуждать
так: «Неважно, как рабочий взял эти
детали, то ли он их получил у кладовщицы
все сразу, то ли он сам набирал эти детали
в тару по очереди (что верно в силу
однородности и симметрии опыта), но раз
есть повторяемость, то почему бы не
применить «формулы Бернулли» с
![]() ».
».
Тогда для
![]() ,
,![]()
![]() ,
,![]() эти студенты получают
эти студенты получают
![]() .
Однако они забывают, что вероятность
взять бракованную деталь
.
Однако они забывают, что вероятность
взять бракованную деталь
![]() верна только для первого испытания. В
последующих испытаниях она изменяется
(становится условной), что нарушает
стационарность и независимость испытаний.
Если бы они знали «схему урн» или
вспомнили о ней, то правильное решение
находится тривиально:
верна только для первого испытания. В
последующих испытаниях она изменяется
(становится условной), что нарушает
стационарность и независимость испытаний.
Если бы они знали «схему урн» или
вспомнили о ней, то правильное решение
находится тривиально:
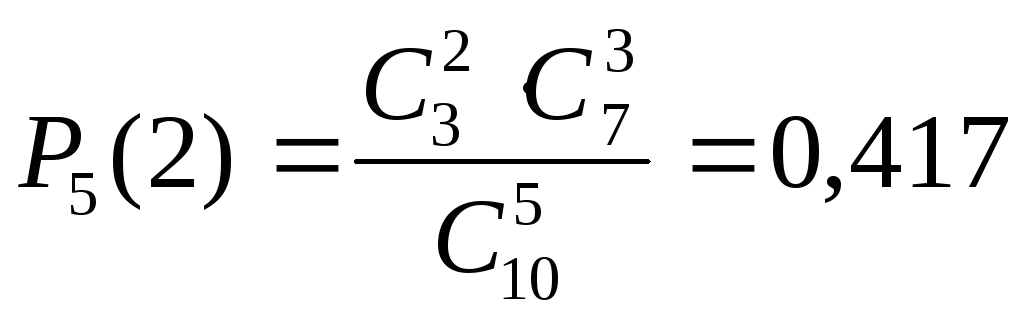 .
.
Заметим, что при
условии «большого» склада
![]()
![]() разница в решении будет несущественной,
так как вероятность изменяется медленно.
Так для значений
разница в решении будет несущественной,
так как вероятность изменяется медленно.
Так для значений
![]() ,
,![]()
![]() ,
,![]() решение по «Бернулли» будет тем же
решение по «Бернулли» будет тем же
![]() ,
а вот правильное:
,
а вот правильное:
 .
.
Разница менее существенна, но студенту остается уповать на «милость» преподавателя.
![]()
