2. Классификация событий

Рассмотрим простейший пример, который мы будем изучать с разных сторон в следующих двух параграфах первой лекции.

________________________

Пример № 1. Бросили игральную (шестигранную) кость (один раз). Найти вероятность того, что выпадет: 1) «»; 2) чётное число; 3) нечётное число; 4) число, меньшее «».

Прелюдия к решению. Рассмотрим следующие элементарные события (возможно, на их основе представим нужные нам события):

- бросили игральную кость и выпала «»;

- бросили игральную кость и выпала «»;

- бросили игральную кость и выпала «»;

- бросили игральную кость и выпала «»;

- бросили игральную кость и выпала «»;

- бросили игральную кость и выпала «».

Теперь легко представить, что:

1) событие , состоящее в том, что бросили игральную кость и выпала «», есть событие , т.е.

;

2) событие , состоящее в том, что бросили игральную кость, а выпало чётное число, представляет собой множество, состоящее из трёх событий,

;

3) событие , состоящее в том, что бросили игральную кость, а выпало нечётное число, представляет собой множество, состоящее из трёх событий,

;

4) событие , состоящее в том, что бросили игральную кость, а выпало число, меньшее «», представляет собой множество, состоящее из четырёх событий,

.

Чтобы научиться находить вероятности сложных событий, нужно провести их классификацию и научиться проводить операции над ними.

_________________________

Определение. Сумма конечного числа событий – событие, состоящее в наступлении хотя бы одного из них.

Пример. В примере № 1 событие равно сумме событий .

________________________

Определение. Произведение конечного числа событий – событие, состоящее в наступлении всех этих событий.

Пример. В примере № 1 событие есть произведение событий и : (математики экономят на знаке произведения).

________________________

Определение. Противоположным событием называется событие, состоящее в не появлении события .

Пример. В примере № 1 событие есть противоположное к событию : .

________________________

Рассмотрим важные для дальнейшего понятия.

Определение. Два события называются несовместными, если наступление одного из них исключает возможность наступления другого. В противоположном случае события называются совместными.

Пример. В примере № 1 события и - несовместные, а события и - совместные.

________________________

Определение. События называются равновозможными (равновероятными), если вероятность наступления каждого из них одна и та же.

Пример. В примере № 1 события и являются равновозможными, если кость сделана без изъянов. Также следует признать равновозможными и события .

________________________

Определение. События называются элементарными, если их наступление нельзя связать с наступлением других событий в этом опыте.

Пример. Извлечение карты «Дама пик» из перемешанной колоды карт – событие элементарное.

________________________

Определение. События называются сложными, если их наступление в опыте можно связать с наступлением других событий в этом опыте.

Пример. Извлечение «пиковой карты» из перемешанной колоды карт – событие сложное, так как его наступление связано с рядом событий в этом опыте, а именно, извлечение «Туз пик», «Король пик», …

_______________________

Определение. События образуют полную группу, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное (отличное от входящих в группу) событие.

Пример. В примере № 1 события и образуют такую полную группу, если не учитывать, что кость при бросании может встать на ребро, исчезнуть (провалиться под пол), …

________________________

Определение. Событие называется достоверным, если оно не может не произойти в условиях данного опыта.

Вероятность достоверного события равна , т.к. для этого события (напомним, что ).

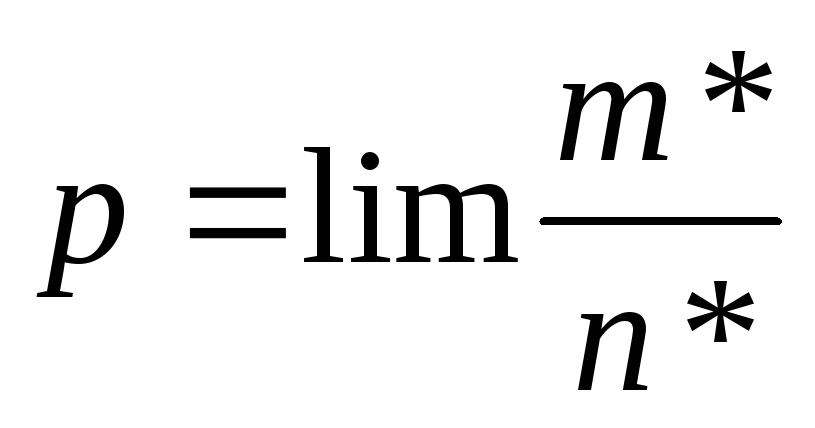Пример. В примере № 1 событие есть как раз такое достоверное событие.

________________________

Определение. Событие, которое не может произойти в условиях данного опыта, называется невозможным событием.

Вероятность невозможного события равна , т.к. для этого события (а ).

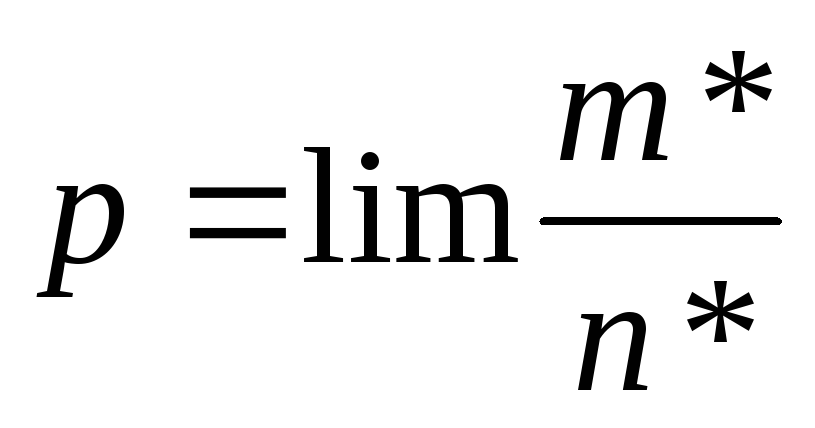Пример. В примере № 1 событие, равное произведению двух событий , является как раз невозможным событием. Невозможное событие представляет собой и событие, состоящее в выпадении .