
- •Арифметические и логические основы вычислительной техники учебное пособие
- •Введение
- •Арифметические основы вычислительной техники Системы счисления
- •Двоичная система счисления
- •Восьмеричная система счисления
- •Шестнадцатеричная система счисления
- •Критерии выбора системы счисления
- •Перевод чисел из одной системы счисления в другую
- •Перевод целых чисел
- •Перевод правильных дробей
- •Перевод чисел из одной системы счисления в другую, основание которой кратно степени 2
- •Кодирование чисел
- •Переполнение разрядной сетки
- •Модифицированные коды
- •Машинные формы представления чисел
- •Погрешность выполнения арифметических операций
- •Округление
- •Нормализация чисел
- •Последовательное и параллельное сложение чисел
- •Сложение чисел с плавающей запятой
- •Машинные методы умножения чисел в прямых кодах
- •Ускорение операции умножения
- •Умножение с хранением переносов
- •Умножение на два разряда множителя одновременно
- •Умножение на четыре разряда одновременно
- •Умножение в дополнительных кодах
- •Умножение на два разряда множителя в дополнительных кодах
- •Матричные методы умножения
- •Машинные методы деления
- •Деление чисел в прямых кодах
- •Деление чисел в дополнительных кодах
- •Методы ускорения деления
- •Двоично-десятичные коды
- •Суммирование чисел с одинаковыми знаками в bcd-коде
- •Суммирование чисел с разными знаками в bcd-коде
- •Система счисления в остаточных классах (сок)
- •Представление отрицательных чисел в сок
- •Контроль работы цифрового автомата
- •Некоторые понятия теории кодирования
- •Обнаружение и исправление одиночных ошибок путем использования дополнительных разрядов
- •Коды Хемминга
- •Логические основы вычислительной техники Двоичные переменные и булевы функции
- •Способы задания булевых функций
- •Основные понятия алгебры логики
- •Основные законы алгебры логики
- •Формы представления функций алгебры логики
- •Системы функций алгебры логики
- •Минимизация фал
- •Метод Квайна
- •Метод Блейка - Порецкого
- •Метод минимизирующих карт Карно (Вейча)
- •Б в Рис. 19. Таблица истинности и карта Карно
- •Минимизация конъюнктивных нормальных форм
- •Минимизация не полностью определенных фал
- •Кубическое задание функций алгебры логики
- •Метод Квайна −Мак-Класки
- •Алгоритм извлечения (Рота)
- •Нахождение множества простых импликант
- •Определение l-экстремалей
- •Минимизация фал методом преобразования логических выражений
- •Применение правил и законов алгебры логики к синтезу некоторых цифровых устройств Синтез одноразрядного полного комбинационного сумматора
- •Синтез одноразрядного комбинационного полусумматора
- •Синтез одноразрядного полного комбинационного сумматора на двух полусумматорах
- •Синтез одноразрядного комбинационного вычитателя
- •Объединенная схема одноразрядного комбинационного сумматора-вычитателя
- •Триггер со счетным входом как полный одноразрядный сумматор
- •Введение в теорию конечных автоматов Основные понятия теории автоматов
- •Способы задания автоматов
- •Структурный автомат
- •Память автомата
- •Канонический метод структурного синтеза автоматов
- •Принцип микропрограммного управления
- •Граф-схема алгоритма
- •Пример синтеза мпа по гса
- •Синтез мпа Мили по гса
- •Синхронизация автоматов
- •Литература
- •220013, Минск, п.Бровки, 6
-
Нахождение множества простых импликант
Преобразование исходного покрытия С0 комплекса К в множество простых импликант Z осуществляется с помощью операции умножения кубов. В результате первого шага (С0*С0) (табл. 16) предусматривается выявление как новых кубов Сy (первой и более высокой размерности), так и кубов, которые не образуют новых кубов (включаются в множество Z0). Из полученных новых кубов образуется множество А1. Также формируется множество В1=С0-Z0. Для следующего шага получения множества Z формируется множество С1=А1U В1. Для уменьшения мощности множества кубов С1 выполним операцию поглощения (удаления) кубов, образующих множество С1, кубами из множества А1 (А1С1).
Таблица 16
|
|
С0*С0 |
х010 |
0х10 |
0000 |
0х01 |
1110 |
1x10 |
|
|
х010 |
- |
|
|
|
|
|
|
|
0х10 |
0010 |
- |
|
|
|
|
|
|
0000 |
00у0 |
00у0 |
- |
|
|
|
|
|
0х01 |
ø |
ø |
000у |
- |
|
|
|
|
1110 |
1у10 |
у110 |
ø |
ø |
- |
|
|
|
1х01 |
ø |
ø |
ø |
ух01 |
ø |
- |
|
|
А1 |
00х0 |
х110 |
000х |
хх01 |
|
|
|
|
1х10 |
|
|
|
|
|
Для рассматриваемого примера получим:


 00х0
00х0
1х10



 00х0 000х
А1
00х0
00х0 000х
А1
00х0
1х10 х110 1х10
А1 = х110 хх01 после выполнения 000х
 000х С1=
х010
операции
С1=
х110
000х С1=
х010
операции
С1=
х110
хх01 0х10 поглощения хх01
0000 В1 х010
Z0=Ø 0х01 0х10
1110
1х01
Среди кубов С0, возможно, находятся такие кубы, которые с кубами множества А1 могут дать новые кубы или оказаться простыми импликантами после второго шага (С1*С1). При формировании таблицы для выполнения операции С1*С1 (табл. 17) следует учесть, что В1*В1 уже выполнялось на шаге С0*С0. Следовательно,
С1*С1=(А1UВ1)*(А1UВ1)=(А1*А1)U(А1*В1)U(В1*А1)U(В1*В1)=(А1*А1)U(А1*В1).
Таблица 17
|
|
С1*С1 |
00х0 |
1х10 |
000х |
х110 |
хх01 |
|
|
00х0 |
- |
|
|
|
|
|
|
1х10 |
у010 |
- |
|
|
|
|
|
000х |
0000 |
ø |
- |
|
|
|
|
х110 |
0у10 |
1110 |
ø |
- |
|
|
|
хх01 |
000у |
ø |
0001 |
ø |
- |
|
|
х010 |
0010 |
1010 |
00у0 |
ху10 |
Ø |
|
|
0х10 |
0010 |
ух10 |
00у0 |
0110 |
Ø |
|
|
А2 |
ø |
хх10 |
ø |
хх10 |
Ø |
В результате выполнения умножения С1*С1 получим:
А2={хх10},
Z1=![]()

 00х0 .
00х0 .
000х
![]()
Необходимо отметить, что куб хх01 не дал нового куба. Но это куб второй размерности и новые кубы может дать на третьем шаге (С2*С2). Поэтому его не следует включать в число кубов, образующих множество Z1.


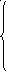
 1х10 хх10
1х10 хх10
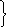
 х110 1х10
х110 1х10
В
C2=А2UB2= =
х010 х010 хх01
0х10 0х10
хх01
Таблица 18
|
|
С2*С2 |
хх10 |
|
|
хх10 |
- |
|
|
хх01 |
Ø |
|
|
А3 |
Ø |
Таким образом, получим А3= Ø, следовательно, новых кубов нет.
Z2=

хх01
В3=С2-Z2= Ø; C3=A3UB3= Ø.
На этом процесс выявления простых импликант окончен.
![]() ,
,

 00х0
00х0
Z=Z0UZ1UZ2= - сформированное
множество простых импликант.
хх01
хх10
Необходимо выяснить, не содержатся ли в этом множестве “лишние” простые импликанты.
