2.5 Роль математических моделей в решении задач оптимального управления

Оптимальное управление работой технической системы связано с целенаправленным её изменением для достижения поставленной цели. Для осуществления оптимального управления должна быть создана работоспособная система управления. Для создания и работы системы управления необходимы информация об объекте, алгоритм обработки информации, средства его реализации для достижения заданных целей управления.

На рис. 2.4 приведена схема оптимального управления.

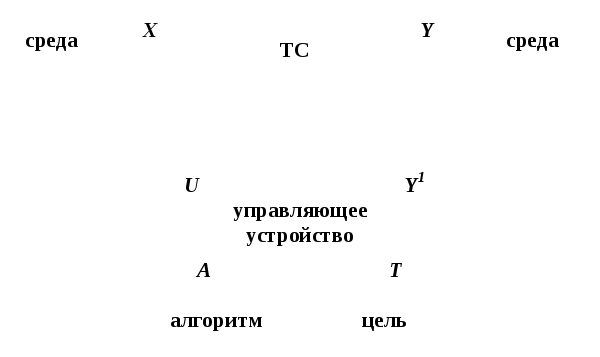
ТС – техническая система – объект управления;

U – управляемая составляющая воздействия среды на систему;

X – неуправляемая составляющая воздействия среды на систему;

Y¹ – информация о состоянии ТС, доступная управляющему устройству: Y¹ < Y;

T – цель, т.е. каким должен быть объект оптимального управления;

A – алгоритм, который показывает, как достичь этой цели.

Рис. 2.4 Схема оптимального управления

Следует отметить, что система управления не обязательно реализуется «в металле». Она может быть реализована в виде системы правил, т.е. в виде алгоритмов, которые реализуются в процессе управления. Любой оператор вместе с объектом, которым он управляет, представляют собой систему управления. Например, шофёр за рулём автомашины образует с ней систему управления. В этом случае органы управления автомашины (руль, педаль газа, тормоз и т.д.) являются теми каналами управления U, с помощью которых шофёр изменяет состояние автомашины Y в желаемом ему направлении Т. В данном случае «управляющее устройство» – шофёр. Он же задаёт цель Т.

Согласно современной теории и практике реализации принципов кибернетики необходимо:

• установить взаимодействие процессов;

• анализировать процессы;

• управлять процессами.

Решение этих задач возможно только тогда, когда известны закономерности превращения входа в выход. Указанные закономерности могут быть представлены в виде математической модели, которую можно описать, проанализировать, обсудить, а её создание требует меньших затрат, чем опыт, основанный на пробах и ошибках.

Современные информационные технологии представляют широчайший арсенал методов моделирования. Прежде всего, это статистические методы, в том числе планирование эксперимента.

Если известен вид преобразователя F, то известна и математическая модель объекта оптимизации. Аналитическое выражение F, т.е. система уравнений, составляет математическое описание системы (процесса).

Для нахождения вида зависимостей параметров системы необходимо иметь алгоритм решения системы уравнений, которой задаётся математическое описание системы.

Математическая модель представляет собой систему уравнений математического описания, которая с помощью определённого алгоритма позволяет прогнозировать поведение объекта при изменении входных (Х) и управляющих (U) параметров.

Для синтеза математической модели необходимы два вида информации:

А – априорная информация об объекте, которая поясняет вид модели и имеет качественный характер.

В – апостериорная информация, т.е. измерительная информация, которая имеет количественный характер:

В = <X, Y>,

где Х – результаты всех измерений входов объекта;

Y – результаты всех измерений его выходов за тот же период наблюдений.

Управление реализуется четвёркой:

< U, I = < X, Y¹ >, A, T,

где U – управляющие воздействия;

I = < X, Y¹ > – информация о состоянии среды и объекта;

А – алгоритм;

Т – цель управления.

Первые три элемента четвёрки зависят от объекта управления и поэтому могут быть определены полностью лишь при наличии модели объекта. Не зная, как U и Х влияют на состояние Y¹, т.е. не имея модели Y¹ = F(X, U), нельзя определить управление U, с помощью которого можно добиться цели Т.

Алгоритм А работы управляющего устройства также зависит от объекта. Как правило, алгоритм управления не может работать без модели объекта. Организация каналов связи управляющего устройства с объектом подчиняется структуре объекта.

Цель управления Т, т.е. переведение объекта в требуемое состояние, разбивается на две цели, соответствующие двум этапам управления:

на первом этапе целью является синтез адекватной модели объекта;

на втором – синтез управления на основе этой модели.