3.5. Методы регулировки передаточных механизмов

Регулировка бывает:

- математической - решение задачи оптимального синтеза по критерию близости f_Теор и f _Ном )

- физической - изменение размеров звеньев с целью установления требуемых значений параметров ПМ: передаточного отношения (чувствительности) , нелинейности , начального положения звеньев и др.

Математическая регулировка.

3.5.1. Регулировка по Методу Наименьших Квадратов (мнк)

Оптимальное соотношение Схемных Парам. чувствительности, нелинейности  и диапазона :

()

Выражение для _CX(х) с учетом (*)

График (кубич. парабола):

Исследование функции _CX(х) позволяет определить корни уравнения при приравнивании _CX(х) нулю:

- ур-е кубич. Параболы

Корни :

Экстремальные значения

_{CX нб} = 0,05 ( /) Dx²

_{CX мах}= 0,022 ( /) Dx²

Точки регулировки выбираем при значениях х, при которых погрешность схемы _CX(х)=0 – это корни уравнения (**)

Минимальное среднеквадратическое значение погрешности схемы приведенное ко входу:

Максимальная относительная нелинейность на Dx :

supreme - «наибольший из наибольших»

Синтез ПМ по МНК обеспечивает «наилучшее» приближение теоретической и номинальной ФП.

Проблема возникает при реализации регулировки приборного ПМ на реальном приборе (при калибровке, ремонте и т.п.). Реальный ПМ имеет еще много составляющих погрешности (технологических и эксплуатационных), которые носят случайный характер. Действительная погрешность ПМ _ПМ(х) для партии приборов определяет зону технолической и эксплуатационной погрешности (См. схему)

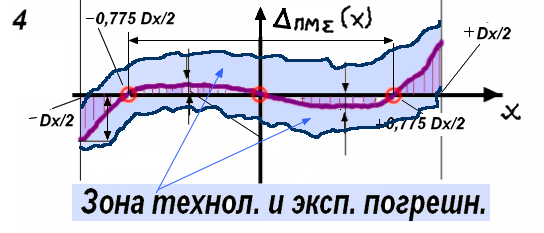
Точки регулировки (т.т. O) находятся внутри диапазона Dx и обеспечить «настройку в ноль» схемной (теоретической) погрешности на фоне других погрешностей очень сложно.

 Поэтому на практике для регулировки выбирают точки регулировки, расположенные на краях и в середине диапазона. Схемная погрешность при этом больше, чем при МНК, но процедура настройки ПМ выполняется проще.

3.5.2. Регулировка по краям диапазона.

Оптимальное соотношение сх. парам. чувствительности, нелинейности и диапазона:

Выражение для _CX(х) с учетом (*)

Экстремальные значения

_{CX мах}= 0,048 ( /) Dx²

Точки регулировки (точки, в которых функция погрешности _CX(х) принимает значение равное нулю) находятся на краях диапазона и в центре диапазона:

Среднеквадратическое значение погрешности схемы :

Максимальная относительная нелинейность:

3.6. Процедура регулировки на примере механизма рзг

1. Задать перемещения входного звена, соответствующие значениям точек регулировки

2. Сравнить положения выходного звена (указателя) с отметками на шкале, соответствующим середине и краям диапазона  Dx/2.

3. Определить несоответствия (погрешности регулировки ПМ) и определить источник погрешности и выполнить регулировку.

Пример. Для Dx = 0.1 мм(0,05) и регулировки по краям.

Для «эталонных» перемещений х применяем концевые меры длины (КМД) и блоки КМД с размерами х₁=10, х₂= 10,05, х₃=10,1мм.

1. чувствительность Кд < К ном

2. чувствительность Кд > К ном

3. чувствительность Кд  К ном, положение точек регулировки смещены в «плюс».

4. и т.п.