3.3. Погрешность схемы пм – критерий качества синтеза пм.

Погрешность схемы _CX (х) – это функция, определяемая разностью f_Теор и f _{Ном .} на диапазоне Dx.

здесь k - номинальная чувствительность,

схемные параметры  - чувствительность,  - нелинейность..

Выбирая различные значения схемных параметров (т.е. размеров звеньев) можно получить разные варианты приближения функции теоретического заменяющего ПМ f_Теор к номинальной ФП f_Ном (графики 1,2,3 и др.) и разные погрешности схемы _CX(х).

Для числовых оценок Погреш. Схемы _CX (х) можно использовать:

1) значения этой функции в отдельных точках (_{CX наиб -,} _{CXмах, -} см. обозначения на графиках).

2) некоторые интегральные характеристики _CX.

Рассмотрим разные варианты приближения f_теор к f _ном.

1-й вариант. Вблизи точки перегиба ФП - хорошее совпадение.

Наибольшая погрешность _{CX наиб} получается на краях диапазона Dx.

Для определения _{CX наиб} подставим х=Dx/2 в выражение для погрешности схемы

Получим

3-й вариант.

Погрешность на краях и в середине равна 0. экстремумы _CXмах меньше, чем _{CX наиб}

2-й вариант. Равномерное приближение по Чебышеву _CXмах=_CXнаиб (МИНИМАКС )

Точечные критерии 1.2,3 – простые, но не всегда эффективные.

4-й вариант. Интегральный критерий- среднее квадратичное значение(СКО) погрешности схемы _CX(х) должно быть минимальным. Название метода – метод наименьших квадратов (М.Н.К.)

Суть МНК : теоретическая ФП f_Теор так расположена относительно номинальной ФП f _Ном,, что среднее значение суммы квадратов отклонений этих функций друг от друга, определенное по всем (n) точкам диапазона Dx, является минимальным.

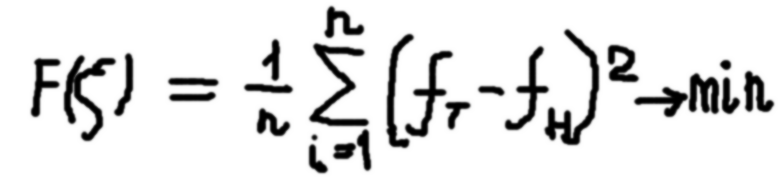- суммирование показано условно, должно быть заменено интегрированием.

3.4. Определение погрешности схемы по мнк.

Задача: определить оценку МНК для погрешности схемы – среднее квадратичное отклонение (С.К.О.) - [_CX(х)].

СКО [х] – это числовая характеристика случайной величины, корень квадратный из дисперсии - меры рассеяния случайной величины.

Здесь Х – измеряемое перемещение в измерительном механизме прибора – случайная величина равновероятно, равномерно распределенная в диапазоне Dx, плотность вероятности распределения р(х) = 1/Dx.

Дисперсия погрешности схемы ²[_CX(х)].:

Для нахождения минимума ²[_CX(х)] (критерий МНК) – приравниваем нулю выражение для производной ²[_CX(х)] по схемному параметру 

После дифференцирования и отбрасывания малозначимых слагаемых получим соотношение :

- оптимальное по МНК соотношение схемных параметров , , номинальной чувствительности k, диапазона преобразования Dx.

С учетом этого соотношения определяют значения схемных параметров, размеры звеньев и диапазон, при котором погрешность схемы (дисперсия ²[_CX(х)]) - минимальная.

Подставив соотношение (*) в выражение для дисперсии, получим СКО погрешности схемы:

 _сх = ² _сх   0,02 Dx³.

Значение СКО  _сх , приведенное ко входу:

 _{сх Х}   0,02( /) Dx³ -

для приведения к входу надо разделить  _сх на чувствительность механизма  .