
- •Тема 1. Определители.
- •Тема 2. Матрицы.
- •Тема 3. Системы линейных уравнений.
- •Глава 2. В е к т о р н а я а л г е б р а
- •Тема 1. Линейные действия с векторами.
- •Тема 2. Умножение векторов.
- •Тема 3. Прямоугольная декартова система координат.
- •Тема 4. Геометрические задачи.
- •Глава 1. Л и н е й н а я а л г е б р а
- •Тема 1. Определители
- •Тема 2. Матрицы
- •Тема 3. Системы линейных уравнений
- •Глава 2. В е к т о р н а я а л г е б р а
- •Тема 1. Линейные действия с векторами
- •Тема 2. Умножение векторов
- •Тема 3. Прямоугольная декартова система координат
- •Тема 4. Геометрические задачи
Тема 2. Умножение векторов.
.
Даны векторы
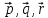 .
Известны модули этих векторов и
углы между ними:
.
Известны модули этих векторов и
углы между ними:
p
=
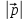 ,
q =
,
q =
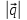 ,
r =
,
r =
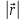 ,
α =
,
α =
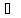
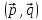 ,
β =
,
β =
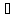
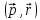 ,
γ =
,
γ =
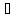
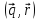 .
Вектор
.
Вектор
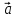 является линейной
является линейной
комбинацией
векторов
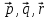 .
Найти модуль вектора
.
Найти модуль вектора
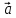 .
.
1.
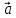 = 2
= 2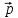 - 3
- 3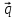 ,
p = 1, q = 2, α =
,
p = 1, q = 2, α =
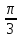 2.
2.
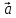 =
=
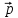 + 2
+ 2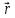 ,
p = 3, r = 1, β =
,
p = 3, r = 1, β =
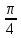
3.
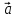 = 2
= 2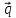 -
-
 ,
q = 4, r = 2, γ =
,
q = 4, r = 2, γ =
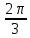 4.
4.
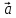 =
=
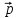 - 2
- 2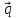 ,
p = 2, q = 1, α =
,
p = 2, q = 1, α =
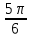
5.
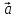 =
=
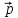 + 2
+ 2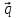 -
-
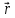 ,
p = 1, q = 1, r = 2, α =
,
p = 1, q = 1, r = 2, α =
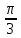 , β =
, β =
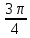 , γ =
, γ =
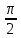
6.
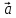 = 2
= 2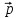 -
-
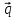 +
+
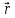 ,
p = 1, q = 2, r = 1, α =
,
p = 1, q = 2, r = 1, α =
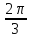 , β =
, β =
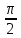 , γ =
, γ =
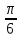
7.
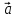 =
=
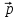 + 2
+ 2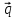 +
+
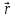 ,
p = 3, q = 1, r = 2, α =
,
p = 3, q = 1, r = 2, α =
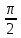 , β =
, β =
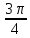 , γ =
, γ =
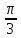
8.
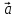 = 2
= 2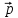 -
-
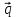 -
-
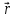 ,
p = 1, q = 2, r = 3, α =
,
p = 1, q = 2, r = 3, α =
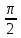 , β =
, β =
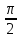 , γ =
, γ =
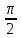
 .
Даны единичные векторы
.
Даны единичные векторы
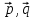 и угол между ними
α =
и угол между ними
α =
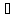
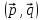 .
Векторы
.
Векторы
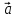 и
и
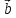
являются
линейными комбинациями векторов
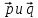 .
На векторах
.
На векторах
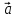 и
и
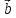 построен
построен
параллелограмм. Найти площадь S этого параллелограмма и длины его диагоналей d1 и d2.


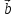


d1
d2

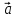
1.
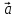 =
=
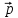 + 3
+ 3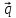 ,
,
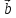 = 3
= 3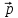 -
-
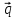 ,
α =
,
α =
 2.
2.
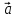 = 3
= 3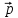 +
+
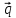 ,
,
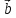 =
=
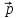 -
-
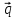 ,
α =
,
α =
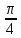
3.
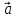 =
=
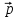 - 2
- 2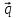 ,
,
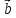 =
=
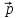 +4
+4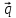 ,
α =
,
α =
 4.
4.
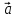 =
=
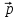 + 3
+ 3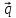 ,
,
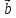 =
=
 - 5
- 5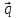 ,
α =
,
α =

5.
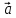 = 2
= 2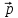 -
-
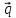 ,
,
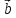 =
=
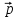 + 3
+ 3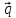 ,
α =
,
α =
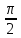 6.
6.
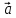 = 3
= 3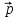 +
+
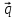 ,
,
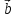 =
=
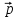 - 5
- 5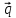 ,
α =
,
α =
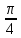
7.
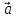 =
=
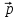 - 4
- 4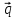 ,
,
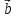 = 3
= 3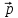 + 2
+ 2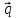 ,
α =
,
α =
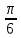 8.
8.
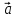 =
=
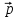 + 4
+ 4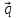 ,
,
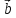 =
=
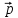 - 2
- 2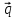 ,
α =
,
α =
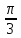
 .
Найти объем параллелепипеда,
построенного на векторах
.
Найти объем параллелепипеда,
построенного на векторах
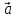 ,
,
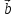 ,
,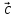 ,
если известны модули этих векторов и
углы между ними:
,
если известны модули этих векторов и
углы между ними:
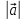 = a,
= a,
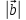 = b,
= b,
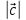 = c, α
=
= c, α
=
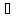
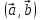 ,
β =
,
β =
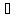
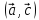 ,
γ =
,
γ =
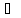
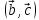 .
.
1.
a = 1,
b =
2, c
=
3,
α =
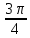 , β =
, β =
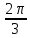 , γ =
, γ =
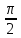 2.
a = 2,
b =
2, c
=
3,
α =
2.
a = 2,
b =
2, c
=
3,
α =
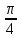 , β =
, β =
 , γ =
, γ =
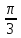
3.
a = 1,
b =
2, c
=
4,
α =
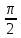 , β =
, β =
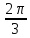 , γ =
, γ =
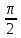 4.
a = 2,
b =
1, c
=
2,
α =
4.
a = 2,
b =
1, c
=
2,
α =
 , β =
, β =
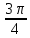 , γ =
, γ =
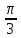
5.
a = 3,
b =
2, c
=
2,
α =
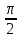 , β =
, β =
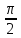 , γ =
, γ =
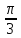 6.
a = 2,
b =
3, c
=
3,
α =
6.
a = 2,
b =
3, c
=
3,
α =
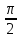 , β =
, β =
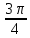 , γ =
, γ =
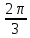
7.
a = 1,
b =
2, c
=
4,
α =
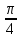 , β =
, β =
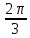 , γ =
, γ =
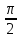 8.
a = 2,
b =
3, c
=
2,
α =
8.
a = 2,
b =
3, c
=
2,
α =
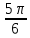 , β =
, β =
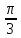 , γ =
, γ =
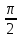
Дополнительные задачи.
1. В квадрат ABCD со стороной a вписана окружность. Точка M - произвольная точка этой окружности. Найти сумму MA2 + MB2 + MC2 + MD2.
2. Около квадрата ABCD со стороной a описана окружность. Точка M - произвольная точка этой окружности. Найти сумму MA2 + MB2 + MC2 + MD2.
3. В куб со стороной a вписана сфера. Точка M - произвольная точка этой сферы. Найти сумму квадратов расстояний от точки M до вершин куба.
4. Найти
отношение объема тетраэдра, построенного
на некомпланарных векторах
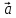 ,
,
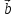 ,
,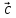 ,
к объему тетраэдра, построенного на
векторах
,
к объему тетраэдра, построенного на
векторах
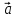 +
+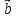 ,
,
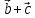 ,
,
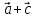 .
.
Тема 3. Прямоугольная декартова система координат.
. Построить
вектор
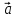
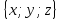 в прямоугольной декартовой системе
координат и указать его направляющие
углы. Найти модуль и направляющие cos-ы
вектора
в прямоугольной декартовой системе
координат и указать его направляющие
углы. Найти модуль и направляющие cos-ы
вектора
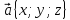 .
.
1.
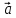
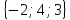 2.
2.
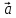
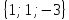 3.
3.
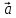
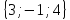 4.
4.
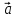
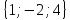
5.
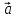
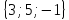 6 .
6 .
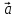
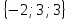 7.
7.
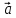
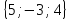 8 .
8 .
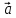
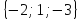
9.
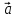
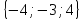 10.
10.
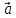
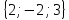 11.
11.
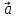
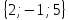 12.
12.
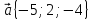
 .
Даны векторы в прямоугольной декартовой
системе координат:
.
Даны векторы в прямоугольной декартовой
системе координат:
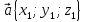 и
и
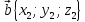 .
Вычислить:
.
Вычислить:
1) скалярное произведение
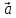
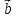
2) проекции
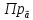
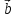 ,
,
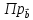
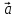
3) векторное произведение
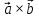
4) площадь параллелограмма, построенного
на этих векторах
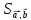
1.
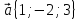 ,
,
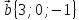 2.
2.
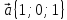 ,
,
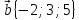 3.
3.
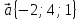 ,
,
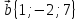
4.
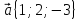 ,
,
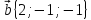 5.
5.
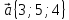 ,
,
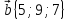 6.
6.
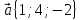 ,
,
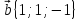
7.
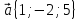 ,
,
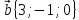 8.
8.
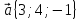 ,
,
 9.
9.
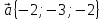 ,
,
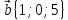
10.
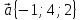 ,
,
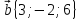 11.
11.
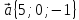 ,
,
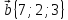 12.
12.
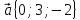 ,
,
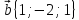
. Даны векторы в прямоугольной декартовой системе координат:
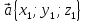 ,
,
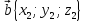 ,
,
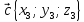 .
Требуется:
.
Требуется:
1) вычислить
смешанное произведение
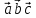 2) определить ориентацию этих
векторов
2) определить ориентацию этих
векторов
3) найти
объем
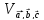 параллелепипеда, построенного на этих
векторах
параллелепипеда, построенного на этих
векторах
1.
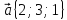 ,
,
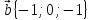 ,
,
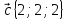 2.
2.
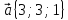 ,
,
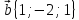 ,
,
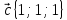
3.
 ,
,
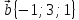 ,
,
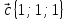 4.
4.
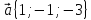 ,
,
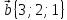 ,
,
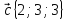
5.
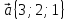 ,
,
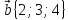 ,
,
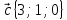 6.
6.
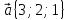 ,
,
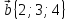 ,
,
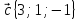
7.
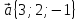 ,
,
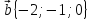 ,
,
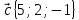 8.
8.
 ,
,
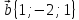 ,
,
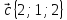
9.
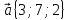 ,
,
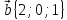 ,
,
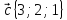 10.
10.
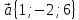 ,
,
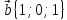 ,
,
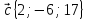
11.
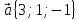 ,
,
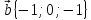 ,
,
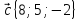 12.
12.
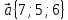 ,
,
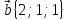 ,
,
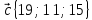
. Даны
векторы
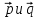 в прямоугольной декартовой системе
координат. Векторы
в прямоугольной декартовой системе
координат. Векторы
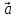 и
и
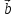
являются линейными комбинациями этих векторов. Определить:
- при каких значениях α и β
векторы
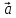 и
и
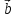 будут коллинеарны (№ 1 ÷
4)
будут коллинеарны (№ 1 ÷
4)
- при каких значениях λ векторы
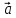 и
и
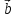 будут ортогональны (№ 5
÷ 8)
будут ортогональны (№ 5
÷ 8)
- при каких значениях λ векторы
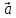 ,
,
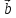 и
и
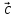 будут компланарны (№ 9 ÷
12)
будут компланарны (№ 9 ÷
12)
1.
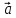 = 2
= 2 + 4
+ 4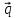 ,
,
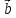 = 3
= 3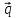 -
-
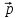 ,
,
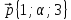 ,
,
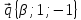
2.
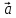 =
=
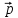 + 2
+ 2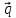 ,
,
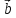 = 3
= 3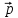 -
-
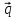 ,
,
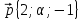 ,
,
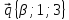
3.
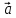 = 5
= 5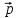 + 3
+ 3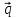 ,
,
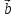 = 2
= 2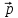 -
-
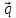 ,
,
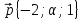 ,
,
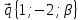
4.
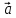 = -2
= -2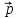 +
+
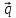 ,
,
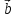 = 3
= 3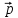 - 2
- 2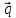 ,
,
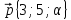 ,
,
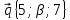
5.
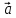 =
=
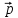 -
-
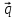 ,
,
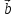 = 4
= 4 + 2
+ 2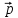 ,
,
 ,
,
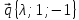
6.
 =3
=3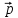 - 2
- 2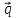 ,
,
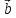 = -2
= -2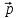 +
+
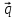 ,
,
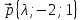 ,
,
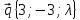
7.
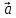 = 2
= 2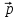 -
-
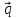 ,
,
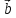 = -
= -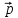 + 3
+ 3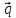 ,
,
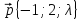 ,
,
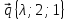
8.
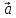 = 2
= 2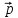 - 3
- 3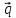 ,
,
 = 2
= 2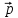 +
+
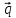 ,
,
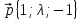 ,
,
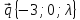
9.
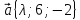 ,
,
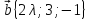 ,
,
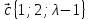
10.
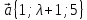 ,
,
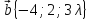 ,
,
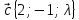
11.
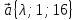 ,
,
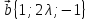 ,
,
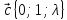
12.
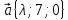 ,
,
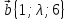 ,
,
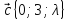
Дополнительные задачи.
1.
Прямоугольная декартова система
координат OXY
на плоскости получена из прямоугольной
декартовой системы координат OXY
параллельным переносом на вектор
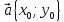 .
Произвольная точка M
на плоскости имеет координаты (x,
y) в одной системе
координат и (x,
y)
- в другой системе координат. Найти связь
между этими координатами.
.
Произвольная точка M
на плоскости имеет координаты (x,
y) в одной системе
координат и (x,
y)
- в другой системе координат. Найти связь
между этими координатами.
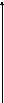
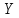
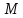
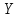
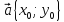 ,
M(x, y),
M(x,
y)
,
M(x, y),
M(x,
y)
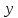

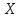
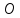
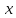


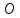
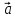

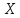
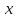
2. Прямоугольная декартова система координат OXY на плоскости получена из прямоугольной декартовой системы координат OXY путем поворота осей на угол . Произвольная точка M на плоскости имеет координаты (x, y) в одной системе координат и (x, y) - в другой системе координат. Найти связь между этими координатами.
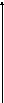
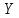
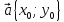 ,
M(x, y),
M(x,
y)
,
M(x, y),
M(x,
y)
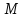
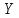
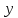

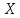

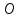
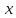
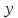


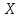
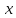

3. Даны
векторы в прямоугольной декартовой
системе координат:
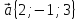 ,
,
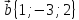 ,
,
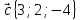 .
Найти координаты вектора
.
Найти координаты вектора
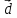 ,
если известно, что
,
если известно, что
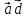 = -5,
= -5,
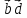 = -11,
= -11,
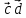 = 20.
= 20.
4. Даны
векторы в прямоугольной декартовой
системе координат:
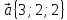 ,
,
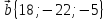 .
Найти координаты вектора
.
Найти координаты вектора
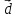 ,
если известно, что
,
если известно, что
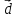
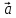 ,
,
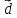
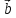 ,
,
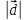 = 14.
= 14.
