
- •Тема 1. Определители.
- •Тема 2. Матрицы.
- •Тема 3. Системы линейных уравнений.
- •Глава 2. В е к т о р н а я а л г е б р а
- •Тема 1. Линейные действия с векторами.
- •Тема 2. Умножение векторов.
- •Тема 3. Прямоугольная декартова система координат.
- •Тема 4. Геометрические задачи.
- •Глава 1. Л и н е й н а я а л г е б р а
- •Тема 1. Определители
- •Тема 2. Матрицы
- •Тема 3. Системы линейных уравнений
- •Глава 2. В е к т о р н а я а л г е б р а
- •Тема 1. Линейные действия с векторами
- •Тема 2. Умножение векторов
- •Тема 3. Прямоугольная декартова система координат
- •Тема 4. Геометрические задачи
З А Д А Ч Н И К
Ч А С Т Ь 1
Л И Н Е Й Н А Я И В Е К Т О Р Н А Я А Л Г Е Б Р А
Глава 1. Линейная алгебра.
Тема 1. Определители.
Тема 2. Матрицы.
Тема 3. Системы линейных уравнений.
Глава 2. Векторная алгебра.
Тема 1. Линейные действия с векторами.
Тема 2. Умножение векторов.
Тема 3. Прямоугольная декартова система координат.
Тема 4. Геометрические задачи.
О Т В Е Т Ы.
Глава 1. Л И Н Е Й Н А Я А Л Г Е Б Р А
Тема 1. Определители.
. Вычислить определители 2-го порядка (довести до числового значения).
1.
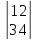 2.
2.
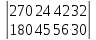 3.
3.
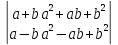
4.
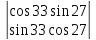 5.
5.
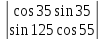 6.
6.
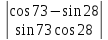
7.
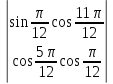 8.
8.
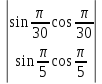 9.
9.
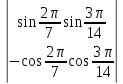
10.
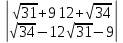 11.
11.
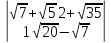 12.
12.
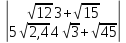
13.
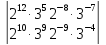 14.
14.
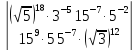
15.
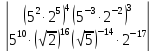 16.
16.

17.
 18.
18.
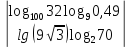
. Вычислить определители 3-го порядка:
− № 1 ÷ 8 - используя разложение по строке или столбцу;
− № 9 ÷ 16 - используя свойства определителей.
1.
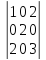 2.
2.
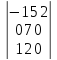 3.
3.
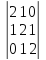 4.
4.
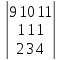
5.
 6.
6.
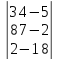 7.
7.
 8.
8.
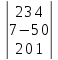
9.
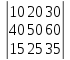 10.
10.
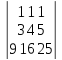 11.
11.
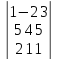 12.
12.
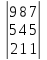
13.
 14.
14.
 15.
15.
 16.
16.

. Вычислить определители 4-го порядка.
1.
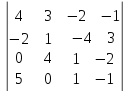 2.
2.
 3.
3.

4.
 5.
5.
 6.
6.

7.
 8.
8.
 9.
9.

Дополнительные задачи.
1. Найти
многочлен: P(λ)
=
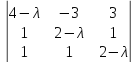 и вычислить его корни.
и вычислить его корни.
2. Для
матрицы A =
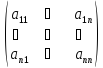 вычислить:
вычислить:
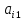
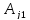 +
+
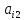
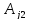 + … +
+ … +
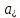
 и
и
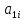
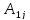 +
+
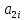
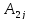 +
+
 +
+
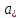
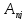 ,
где i ≠ j
(
,
где i ≠ j
(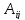 - алгебраическое дополнение элемента
- алгебраическое дополнение элемента
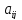 ).
).
Вычислить определители n -го порядка:
3.
 4.
4.
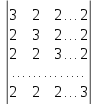 5.
5.
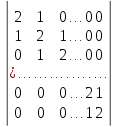
6.
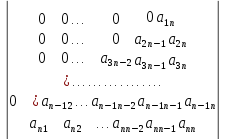 7.
7.
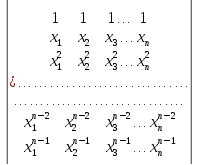
 8.
8.
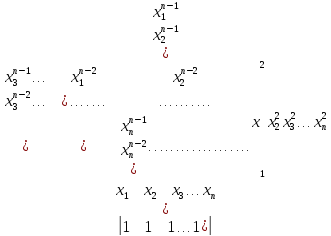 9.
9.

10.
 11.
11.
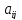 = min
{i,j}
12.
= min
{i,j}
12.
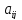 = max
{i,j}
= max
{i,j}
Тема 2. Матрицы.
 .
Выполнить действия над матрицами.
.
Выполнить действия над матрицами.
1.
(3A - 2B)C
= ? A =
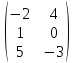 ,
B =
,
B =
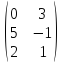 ,
C =
,
C =

2.
B(A
+ 3C) = ? A =
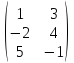 ,
B=
,
B=
 ,
C =
,
C =
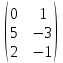
3.
A(2E
+ 3B) = ? A =
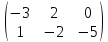 ,
B =
,
B =
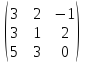
4.
(2A - 3E)B
= ? A =
 ,
B =
,
B =
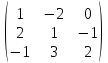
5.
AB
- BA
= ? A =
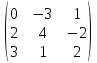 ,
B =
,
B =
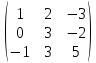
6.
f(A) = ? f(x) = 3x2
- 2x + 3, A =
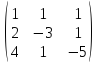
7.
f(A) = ? f(x) = -2x2
+ 3x - 5, A =
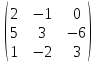
8.
f(A) = ? f(x) = -2x2
- 3x + 2, A =
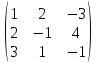
9.
f(A) = ? f(x) = 3x2
+ 2x - 4, A =
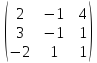
10.
f(A) = ? f(x) = 2x2
- 4x + 3, A =
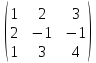
. Найти обратную матрицу A-1 и сделать проверку.
1.
A =
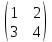 2.
A =
2.
A =
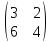 3.
A =
3.
A =
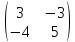 4.
A =
4.
A =
5.
A =
 6.
A =
6.
A =
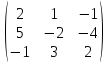 7.
A =
7.
A =
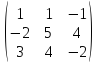 8.
A =
8.
A =
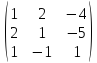
. Найти ранг матрицы.
1.
A =
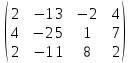 2.
A =
2.
A =

3.
A =
 4.
A =
4.
A =
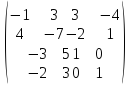
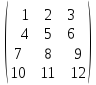
5.
A =
 6.
A =
6.
A =

7.
A =
 8.
A =
8.
A =
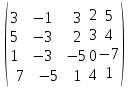
9.
A =
 10.
A =
10.
A =
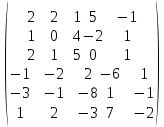
Дополнительные задачи.
Вычислить:
1.
 2.
2.
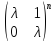 3.
3.
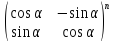
Найти обратные матрицы для матрицы A n-го порядка:
4. A
=
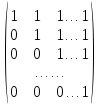 5. A =
5. A =
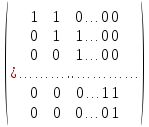
6. A
=

7. Составить многочлен: P (x) = det (A - xE) - и найти его корни, если
A
=
 - заданная треугольная матрица, E
- единичная матрица порядка n.
- заданная треугольная матрица, E
- единичная матрица порядка n.
8. Составить многочлен: P (λ) = det(A - λE) - и найти его корни, если
A
=
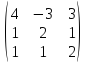 ,
E - единичная
матрица 3-го порядка.
,
E - единичная
матрица 3-го порядка.
9. Найти
x из условия: A2
=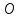 ,
где A =
,
где A =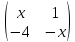 ,
,
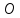 - нулевая матрица 2-го порядка.
- нулевая матрица 2-го порядка.
10. Найти
все решения матричного уравнения: X
2 =
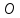 ,
где X - матрица 2-го порядка.
,
где X - матрица 2-го порядка.
11. Найти
x из условия: A2
= E, где A
=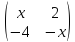 ,
E - единичная матрица 2-го порядка.
,
E - единичная матрица 2-го порядка.
12. Найти все решения матричного уравнения: X 2 = E, где X - матрица 2-го порядка.
