
- •1 Вопрос
- •2 Вопрос
- •3 Вопрос
- •4 Вопрос
- •Теорема о необходимом и достаточном условии существования предела последовательности:
- •Свойства бесконечно малых и бесконечно больших последовательностей:
- •5 Вопрос
- •Монотонная функция:
- •6 Вопрос
- •Функция синус
- •Функция косинус
- •Функция тангенс
- •Функция котангенс
- •7 Вопрос
- •8 Вопрос
- •9 Вопрос
- •10 Вопрос
- •11 Вопрос
- •12 Вопрос
- •13 Вопрос
7 Вопрос
Предел функции в точке:
На ε-δ языке:
Число
ε называется lim f
при x→a,
если
![]()
На языке последовательностей:
Число
A называют lim
f(x) при x→a,
если
![]()
На языке окрестностей:
Число
A называют пределом f(x)
при x→a,
если
![]()
Односторонние пределы:
Число
A называется пределом
функции f(x)
при x→a
справа, если
![]()
Число A называется пределом функции f(x) при x→a слева, если
![]()
Предел
функции при
![]() :
:
Число
A называется пределом
функции f(x)
при x→![]() ,
если
,
если
![]()
8 Вопрос
Свойства функций, имеющих предел в точке:
Локальная ограниченность:
Если
f(x) имеет
lim в точке a,
то существует
![]() и
число k такие, что
и
число k такие, что
![]()
Доказательство:
по Коши: пусть lim f(x)
= A при х→a.
Возьмем
![]() =1.
По определению предела для
=1.
По определению предела для
![]() существует
существует
![]()
Cохранение знака:
lim
f(x) = A, A![]() 0
при x→a,
тогда
0
при x→a,
тогда
![]()
1.
![]()
2.
![]()
Доказательство:
Возьмем
![]() .
По Коши:
.
По Коши:
![]() ,
т.к.
,
т.к.
![]()
![]()
-
Если A>0, то
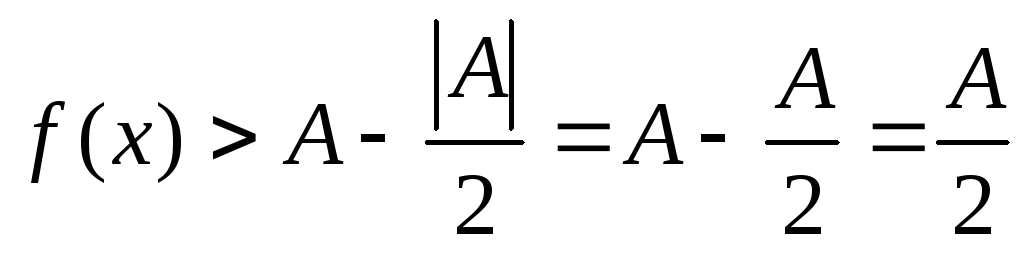
-
Если A<0, то
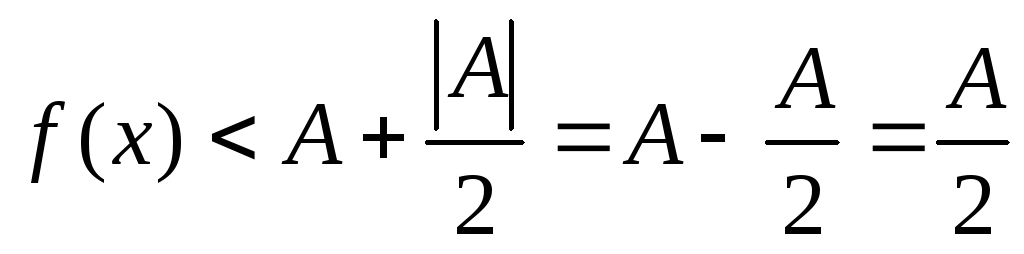
Переход к пределу в неравенствах:
Пусть
в некоторой
![]() при x→a,
тогда
при x→a,
тогда
![]()
Доказательство:
по Гейне: xn→a,
xn![]() a.
Построим две последовательности:
a.
Построим две последовательности:
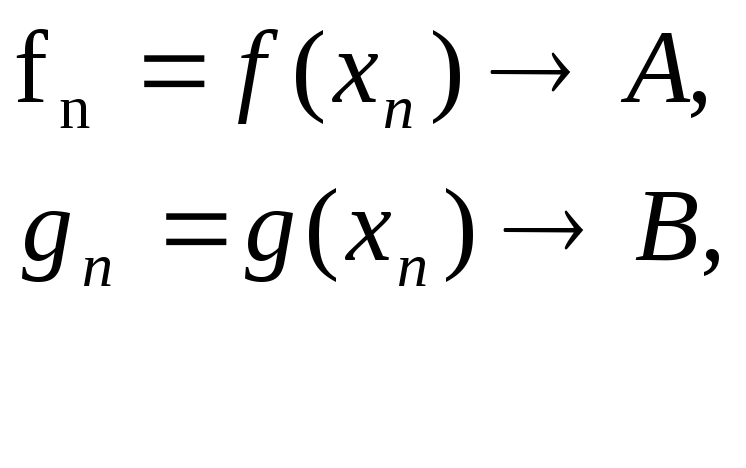
По
условию:![]() ,
,
![]()
Арифметические операции:
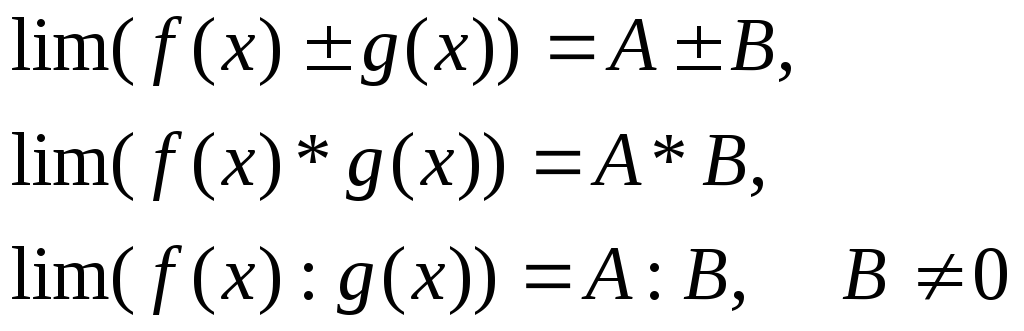
Доказательство:
по Гейне:
![]()
![]()
Дальнейшее доказательство очевидно.
9 Вопрос
Бесконечно
малая: если
![]() .
.
Бесконечно
большая: если
![]()
Свойства:
1.
Если
![]() - б.м. при x→a,
- б.м. при x→a,
![]()
![]() ,
то
,
то
![]() - б.б.
- б.б.
Доказательство:
![]() - б.б.
- б.б.
2.
Если
![]() - б.б. при x→a,
- б.б. при x→a,
![]()
![]() ,
то
,
то
![]() - б.м.
- б.м.
Доказательство: Аналогично первому.
3.
Если
![]() -
б.м. при x→a,
а g(x) –
ограниченная, то
-
б.м. при x→a,
а g(x) –
ограниченная, то
![]() *g(x)
– б.м. последовательность при x→a.
*g(x)
– б.м. последовательность при x→a.
Доказательство:
![]() = x – б.м., x→0.
= x – б.м., x→0.
10 Вопрос
Определения непрерывности функции в точке:
Функция
f(x) называется
непрерывной в точке a,
если
![]()
Функция
f(x) называется
непрерывной в точке a,
если
![]()
Функция
f(x) называется
непрерывной в точке a,
если
![]()
Функция f(x) называется непрерывной в точке a для любой последовательности xn→a, значение функции которой стремится к а. (f(xn)) →a)
Функция
f(x) называется
непрерывной в точке a,
если
![]()
Свойства функций, непрерывных в точке:
Арифметические: сложение, вычитание, умножение, деление.
Доказательство:
Если функции f
и g
непрерывны в точке a,
то следует из свойств пределов функции
в точке и непрерывности точке:
![]()
Непрерывность
сложной функции: если f(x)
непрерывна в точке a, а
функция g(x)
непрерывна в точке
![]() ,
такое, что a = g(
,
такое, что a = g(![]() ),
то сложная функция F(t)=f(g(t))
непрерывна в точке
),
то сложная функция F(t)=f(g(t))
непрерывна в точке
![]()
Доказательство:

Локальная
ограниченность функции в ограниченной
точке: если функция f
непрерывна в точке, то она ограничена
в окрестности данной точки f
в точке a и
![]() и число k такое, что
и число k такое, что
![]()
Сохранение
знака: если f непрерывна
в точке a и f(a)
![]() ,
то существует окрестность точки a,
то
,
то существует окрестность точки a,
то
![]() такая,
что
такая,
что
![]()
1.
![]()
2.
![]()
11 Вопрос
Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
-
Существуют левосторонний предел
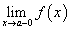 и
правосторонний предел
и
правосторонний предел 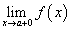 ;
; -
Эти односторонние пределы конечны.
При этом возможно следующие два случая:
-
Левосторонний предел и правосторонний предел равны друг другу:
![]()
Такая точка называется точкой устранимого разрыва.
-
Левосторонний предел и правосторонний предел не равны друг другу:
![]()
Такая
точка называется точкой
конечного разрыва.
Модуль разности значений односторонних
пределов![]() называется скачком
функции.
называется скачком
функции.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
