
- •1 Вопрос
- •2 Вопрос
- •3 Вопрос
- •4 Вопрос
- •Теорема о необходимом и достаточном условии существования предела последовательности:
- •Свойства бесконечно малых и бесконечно больших последовательностей:
- •5 Вопрос
- •Монотонная функция:
- •6 Вопрос
- •Функция синус
- •Функция косинус
- •Функция тангенс
- •Функция котангенс
- •7 Вопрос
- •8 Вопрос
- •9 Вопрос
- •10 Вопрос
- •11 Вопрос
- •12 Вопрос
- •13 Вопрос
1 Вопрос
Последовательность:
это набор элементов некоторого множества:
-
для каждого натурального числа можно указать элемент данного множества;
-
это число является номером элемента и обозначает позицию данного элемента в последовательности;
-
для любого элемента (члена) последовательности можно указать следующий за ним элемент последовательности.
Ограниченная последовательность - члены которой образуют ограниченное множество.
Ограниченное
множество. 1. Множество
действительных чисел называется
ограниченным, если существует
такое число М > 0, что для любого
элемента х данного множества
справедливо неравенство
![]() .
Множество называется ограниченным
сверху (снизу), если существует
такое число Р, что для любого
элемента х данного множества имеет
место неравенство
.
Множество называется ограниченным
сверху (снизу), если существует
такое число Р, что для любого
элемента х данного множества имеет
место неравенство
![]() (соответственно
(соответственно
![]() ).
).
Неограниченная последовательность — это последовательность, которая не является ограниченной.
Монотонная последовательность — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают. Подобные последовательности часто встречаются при исследованиях и имеют ряд отличительных особенностей и дополнительных свойств. Последовательность из одного числа не может считаться возрастающей или убывающей.
2 Вопрос
Сходящиеся последовательности:
Определение. Последовательность {xn} называется сходящейся, если существует такое вещественное число а, что последовательность {xn−a} является бесконечно малой. Если последовательность {xn→a } является сходящейся и имеет своим пределом число a, то символически это записывают так: lim xn=a или xn→a при n→∞ n→∞
Определение. Последовательность {xn} называется сходящейся, если существует такое вещественное число a, что для любого положительного вещественного числа ε найдется номер N(ε) такой, что при всех n>N элементы xn этой последовательности удовлетворяют неравенству ∣xn−a∣<ε При этом число a называется пределом последовательности. Неравенство (5) можно записать в эквивалентной форме −ε<xn−a<+ε или, a−ε<xn<a+ε . (5') Определение. Последовательность {xn} называется сходящейся, если существует такое число a, что в любой ε-окрестности точки aнаходятся все элементы последовательности {xn} начиная с некоторого номера (зависящего от ε).
Сходящаяся последовательность имеет только один предел:
Предположим, что два вещественных числа а и b являются пределами сходящейся последовательности {xn}. xn=a+an и xn=b+bn, где {an} и {bn} - некоторые бесконечно малые последовательности. Получим an−bn=b−a . Последовательность {an−bn} является бесконечно малой, а в силу равенства an−bn=b−a все элементы этой бесконечно малой последовательности равны одному и тому же вещественному числу b−a . Число b−a равно нулю, т. е. b=a. Теорема доказана.
Всякая сходящаяся последовательность является ограниченной:
Доказательство. Пусть {xn} - сходящаяся последовательность и a ее предел. Фиксируем некоторое положительное число ε и по нему номер N такой, что ∣xn−a∣<ε при n≥N или, a−ε<xn<a+ε при n≥N . Обозначим через A наибольшее из следующих (N+1) чисел: ∣a−ε∣,∣a+ε∣,∣∣x1∣∣,∣∣x2∣∣,...,∣∣хN−1∣∣ . Тогда, очевидно, ∣xn∣≤A для всех номеров n, а это и доказывает ограниченность последовательности {xn}. Теорема доказана.
Переход к пределу в неравенствах:
Доказывается через ε-окрестности по рисунку:
Если xn≥yn и lim xn=a и limyn=b при x→∞, то:
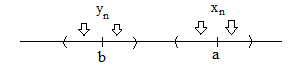
Т.е. a>b. Доказано.
Сохранение знака предела:
Пусть lim xn = a ≠ 0 при x→∞, тогда существует n0 такое, что для всех n > n0:
-
xn >
 ,
a>0,
,
a>0, -
xn <
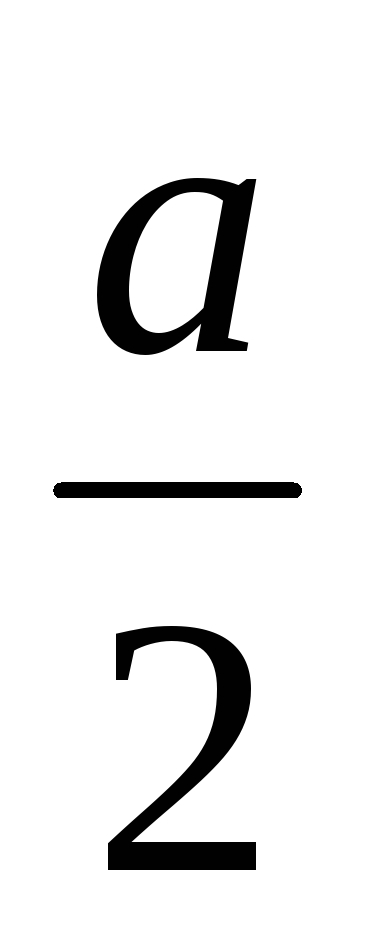 ,
a<0.
,
a<0.
Доказательство:
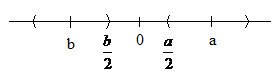
Возьмем
ε =
![]() > 0.
> 0.
![]() n0 ,
n0 ,
![]() n>n0,
n>n0,
-![]() < xn
– a <
< xn
– a <
![]() => a -
=> a -
![]() < xn
< a +
< xn
< a +
![]()
1. a > 0:
xn
> a -
![]() = a -
= a -
![]() =
=
![]()
2. a < 0:
Xn
< a +
![]() < a -
< a -
![]() =
=
![]()
