
- •Система отсчета. Кинематика материальной точки. Траектория и путь. Перемещение, скорость и ускорение материальной точки.
- •Криволинейное движение. Скорость и ускорение (нормальное, тангенциальное) при криволинейном движении.
- •Прямолинейное (равномерное и равноускоренное) движение. Графики зависимости координаты и скорости от времени.
- •Движение материальной точки по окружности. Угловая скорость и угловое ускорение. Равномерное и равноускоренное вращательные движения. Связь между линейными и угловыми величинами.
- •Первый закон Ньютона. Инерциальные системы отсчета. Принцип относительности Галилея, преобразования Галилея. Закон сложения скоростей.
- •Взаимодействие тел, сила, масса. Второй закон Ньютона. Виды силовых взаимодействий. Силы упругости, трения, тяготения.
- •Третий закон Ньютона. Импульс. Изолированная система. Закон сохранения импульса.
- •Неинерциальные системы отсчета. Силы инерции в поступательных и во вращательных неинерциальных системах отсчета.
- •Центр масс. Теорема о движении центра масс.
- •Движение тела переменной массы. Уравнение Мещерского.
- •Движение в центральном поле сил. Законы Кеплера и закон всемирного тяготения.
- •Консервативные и неконсервативные силы. Работа консервативных сил. Потенциальная энергия.
- •Связь между силой и потенциальной энергией. Потенциальные энергии силы тяжести, силы упругости и силы гравитационного взаимодействия.
- •Механическая работа и кинетическая энергия. Механическая энергия системы тел. Закон сохранения механической энергии.
- •Соударение двух тел. Абсолютно упругий и абсолютно неупругий удар.
- •Момент импульса и момент силы относительно неподвижного начала. Уравнение моментов.
- •Уравнение моментов. Закон сохранения момента импульса.
- •Момент импульса и момент силы относительно неподвижной оси. Уравнение динамики вращательного движения относительно неподвижной оси.
- •Инерция при вращательном движении. Момент инерции. Кинетическая энергия твердого тела при вращательном движении.
- •Моменты инерции симметричных тел (цилиндр, шар). Теорема Штейнера. Пример применения.
- •(21)Гидростатика. Закон Паскаля. Закон Архимеда. Основное уравнение гидростатики.
- •(22) Стационарное движение идеальной жидкости. Уравнение Бернулли.
- •Гармонические колебания. Основные характеристики гармонических колебаний: амплитуда, фаза, частота, период.
- •Комплексная форма гармонических колебаний. Сложение гармонических колебаний одинаковых и близких частот. Биения.
- •Гармонический осциллятор. Уравнение динамики гармонических колебаний. Примеры гармонических осцилляторов: пружинный, физический и математический маятники.
- •Затухающие колебания. Коэффициент затухания, время релаксации. Логарифмический декремент затухания.
- •Вынужденные колебания. Амплитуда и фаза вынужденных колебаний. Резонанс. Резонансные характеристики осциллятора (добротность, избирательность).
- •29 Принцип суперпозиции. Интерференция волн. Стоячие волны.
- •(30) Эффект Доплера. Его применение.
-
Система отсчета. Кинематика материальной точки. Траектория и путь. Перемещение, скорость и ускорение материальной точки.
Материа́льная то́чка — простейшая физическая модель в механике — математическая абстракция — тело, размеры которого допустимо считать бесконечно малыми по отношению к остальным объектам исследуемой задачи.
Система отсчёта — это совокупность тела отсчёта, системы координат и системы отсчёта времени, связанных с этим телом, по отношению к которому изучается движение (или равновесие) каких-либо других материальных точек или тел.
Математически движение тела (или материальной точки) по отношению к выбранной системе отсчёта описывается уравнениями, которые устанавливают, как изменяются с течением времени t координаты, определяющие положение тела (точки) в этой системе отсчёта. Эти уравнения называются уравнениями движения. Например, в декартовых координатах х, y, z движение точки определяется уравнениями x = f1(t), y = f2(t), z = f3(t).
Скорость
- векторная физическая величина,
характеризующая быстроту перемещения
и направление движения материальной
точки в пространстве относительно
выбранной системы отсчёта (например,
угловая скорость). Этим же словом может
называться скалярная величина, точнее
модуль производной радиус-вектора.
![]()
Ускорение
- производная скорости по времени,
векторная величина, показывающая,
насколько изменяется вектор скорости
точки (тела) при её движении за единицу
времени (т.е. ускорение учитывает не
только изменение величины скорости, но
и её направления).
![]()
Перемеще́ние
(в кинематике) — изменение местоположения
физического тела в пространстве
относительно выбранной системы отсчёта.
Также перемещением называют вектор,
характеризующий это изменение. Обладает
свойством аддитивности. Длина отрезка
— это модуль перемещения, измеряется
в метрах (СИ). Можно определить перемещение,
как изменение радиус-вектора точки: .
![]()
-
Криволинейное движение. Скорость и ускорение (нормальное, тангенциальное) при криволинейном движении.
Движение материальной точки полностью определяется изменением её координат во времени (например, двух на плоскости). Изучением этого занимается кинематика точки. В частности, важными характеристиками движения являются траектория материальной точки, перемещение, скорость и ускорение.
Прямолинейное движение точки (когда она всегда находится на прямой, скорость параллельна этой прямой)
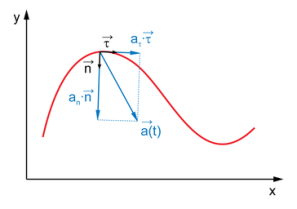
Криволинейное движение - это движение точки по траектории, не представляющей собою прямую, с произвольным ускорением и произвольной скоростью в любой момент времени (например, движение по окружности).
Тангенциа́льное
ускоре́ние — компонента ускорения,
направленная по касательной к траектории
движения. Совпадает с направлением
вектора скорости при ускоренном движении
и противоположно направлено при
замедленном. Характеризует изменение
модуля скорости. Обозначается обычно
![]()
-
Прямолинейное (равномерное и равноускоренное) движение. Графики зависимости координаты и скорости от времени.
Равноускоренное движение — движение, при котором ненулевой вектор ускорения остаётся неизменным по модулю и направлению.
При равноускоренном движении по прямой скорость тела определяется формулой: v(t) = v0 + at
Зная,
что![]() , найдём формулу для определения
координаты x:
, найдём формулу для определения
координаты x:![]()
Равноме́рное
движе́ние — механическое движение, при
котором тело за любые равные отрезки
времени проходит равные перемещения.
Равномерное движение материальной
точки — это движение, при котором
скорость точки остаётся неизменной.
Перемещение, пройденное точкой за время![]() , задаётся в этом случае формулой
, задаётся в этом случае формулой![]() .
.
